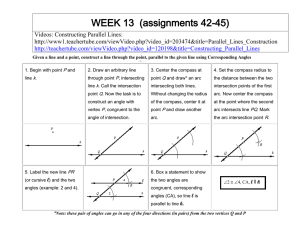
geometry star test study guide
... circle, circle that circumscribes a polygon. Important Theorems/Properties: We had many theorems in this chapter that might appear on the STAR test, but the most important ones are: If a line is tangent to a circle, then it is perpendicular to the radius at the pt. of tangency. If 2 tangent line ...
... circle, circle that circumscribes a polygon. Important Theorems/Properties: We had many theorems in this chapter that might appear on the STAR test, but the most important ones are: If a line is tangent to a circle, then it is perpendicular to the radius at the pt. of tangency. If 2 tangent line ...
Geometry DIG - Prescott Unified School District
... that two triangles are congruent if and only if corresponding pairs of sides and corresponding pairs of angles are congruent. Connection: 9-10.WHST.1e HS.G-CO.B.8. Explain how the criteria for triangle congruence (ASA, SAS, and SSS) follow from the definition of congruence in terms of rigid motions. ...
... that two triangles are congruent if and only if corresponding pairs of sides and corresponding pairs of angles are congruent. Connection: 9-10.WHST.1e HS.G-CO.B.8. Explain how the criteria for triangle congruence (ASA, SAS, and SSS) follow from the definition of congruence in terms of rigid motions. ...
Lecture 1: Trigonometric Functions: Definitions
... equation x2 + y 2 = 1. In fact, choosing any point on C determines such a triangle. If (a, b) is a point on C, the acute angle θ determined by (a, b) is the angle between the line from (a, b) to the origin and the x-axis. Instead of measuring this with degrees, we will now measure the angle by the d ...
... equation x2 + y 2 = 1. In fact, choosing any point on C determines such a triangle. If (a, b) is a point on C, the acute angle θ determined by (a, b) is the angle between the line from (a, b) to the origin and the x-axis. Instead of measuring this with degrees, we will now measure the angle by the d ...
Riemannian connection on a surface

For the classical approach to the geometry of surfaces, see Differential geometry of surfaces.In mathematics, the Riemannian connection on a surface or Riemannian 2-manifold refers to several intrinsic geometric structures discovered by Tullio Levi-Civita, Élie Cartan and Hermann Weyl in the early part of the twentieth century: parallel transport, covariant derivative and connection form . These concepts were put in their final form using the language of principal bundles only in the 1950s. The classical nineteenth century approach to the differential geometry of surfaces, due in large part to Carl Friedrich Gauss, has been reworked in this modern framework, which provides the natural setting for the classical theory of the moving frame as well as the Riemannian geometry of higher-dimensional Riemannian manifolds. This account is intended as an introduction to the theory of connections.