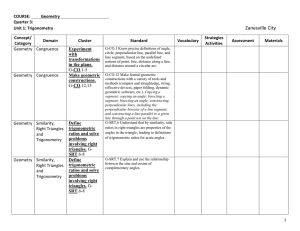
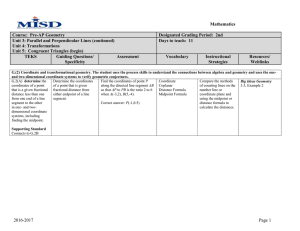
Chapter 4-One Way to Go: Euclidean Geometry of the Plane
... without making any assumptions about parallel lines Geometers were trying to extend neutral geometry to include all of Euclidean but none ever succeeded Because several people were able to show Euclid’s 5th postulate is independent ...
... without making any assumptions about parallel lines Geometers were trying to extend neutral geometry to include all of Euclidean but none ever succeeded Because several people were able to show Euclid’s 5th postulate is independent ...
Glossary
... (p. 506) A type of transformation, with center C and scale factor k, that maps every point P in the plane to a point P§ so that the following two properties are true. (1) If P is not Æ˘ the center point C, then the image point P§ lies on CP . The scale factor k is a positive number such that CP§ = k ...
... (p. 506) A type of transformation, with center C and scale factor k, that maps every point P in the plane to a point P§ so that the following two properties are true. (1) If P is not Æ˘ the center point C, then the image point P§ lies on CP . The scale factor k is a positive number such that CP§ = k ...
2 - SchoolRack
... circle from an exterior point, then the product of the measures of one secant segment and its external secant segment is equal to the product of the measures of the other secant segment and its external secant segment. ...
... circle from an exterior point, then the product of the measures of one secant segment and its external secant segment is equal to the product of the measures of the other secant segment and its external secant segment. ...
Least–squares Solution of Homogeneous Equations
... We derive: 2A>Ah − 2λh = 0. After some manipulation we end up with: (A>A − λE)h = 0 which is the characteristic equation. Hence, we know that h is an eigenvector of (A>A) and λ is an eigenvalue. The least-squares error is e = h>A>Ah = h>λh. The error will be minimal for λ = mini λi and the sought so ...
... We derive: 2A>Ah − 2λh = 0. After some manipulation we end up with: (A>A − λE)h = 0 which is the characteristic equation. Hence, we know that h is an eigenvector of (A>A) and λ is an eigenvalue. The least-squares error is e = h>A>Ah = h>λh. The error will be minimal for λ = mini λi and the sought so ...
Chapter 7: Proportions and Similarity
... SKYSCRAPERS Josh wanted to measure the height of the Sears Tower in Chicago. He used a 12-foot light pole and measured its shadow at 1 p.m. The length of the shadow was 2 feet. Then he measured the length of the Sears Tower’s shadow and it was 242 feet at the same time. What is the height of the Se ...
... SKYSCRAPERS Josh wanted to measure the height of the Sears Tower in Chicago. He used a 12-foot light pole and measured its shadow at 1 p.m. The length of the shadow was 2 feet. Then he measured the length of the Sears Tower’s shadow and it was 242 feet at the same time. What is the height of the Se ...
Arc – an unbroken part of the circle. Two endpoints are always the
... Common Interior Tangent – do not _________________________. ...
... Common Interior Tangent – do not _________________________. ...
Day 1 Day 2 Day 3 Day 4 Day 5 Day 6 Day 7 Day 8 Day 9 Day 10
... Day 3 Find the distance of a line segment on a number line. Measure and find the midpoint of a line segment using a ruler. Find the midpoint of a line segment on a number line. Use segment bisector to find unknown variables. ...
... Day 3 Find the distance of a line segment on a number line. Measure and find the midpoint of a line segment using a ruler. Find the midpoint of a line segment on a number line. Use segment bisector to find unknown variables. ...
Riemannian connection on a surface

For the classical approach to the geometry of surfaces, see Differential geometry of surfaces.In mathematics, the Riemannian connection on a surface or Riemannian 2-manifold refers to several intrinsic geometric structures discovered by Tullio Levi-Civita, Élie Cartan and Hermann Weyl in the early part of the twentieth century: parallel transport, covariant derivative and connection form . These concepts were put in their final form using the language of principal bundles only in the 1950s. The classical nineteenth century approach to the differential geometry of surfaces, due in large part to Carl Friedrich Gauss, has been reworked in this modern framework, which provides the natural setting for the classical theory of the moving frame as well as the Riemannian geometry of higher-dimensional Riemannian manifolds. This account is intended as an introduction to the theory of connections.