tpc maths (part a) - nswtmth307a
... 1. Line up the base line of the protractor with one arm of the angle (the arms of the angle may have to be extended). 2. Line up the vertical centre line with the apex of the angle. 3. Read off the scale in degrees – check whether the angle is acute or obtuse and make sure that you read off the corr ...
... 1. Line up the base line of the protractor with one arm of the angle (the arms of the angle may have to be extended). 2. Line up the vertical centre line with the apex of the angle. 3. Read off the scale in degrees – check whether the angle is acute or obtuse and make sure that you read off the corr ...
unit 1: review of part 1 material
... 1. Splits the segment into two congruent marks and has two segments that meet at a right angle. 2. Steps a) Copy the segment b) Create an arc that is more than half of the segment but less then the full segment in length. Draw this arc twice (once from each of the ends). c) Connect the intersection. ...
... 1. Splits the segment into two congruent marks and has two segments that meet at a right angle. 2. Steps a) Copy the segment b) Create an arc that is more than half of the segment but less then the full segment in length. Draw this arc twice (once from each of the ends). c) Connect the intersection. ...
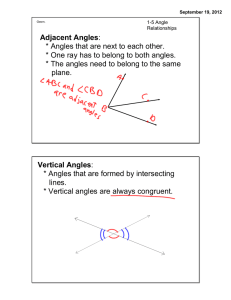
Prove the AA Similarity Theorem
... Provide feedback to the student concerning any errors or omissions and allow the student to revise his or her proof. Consider implementing the MFAS task Justifying a Proof of the AA Similarity Theorem (G-SRT.1.3) for further experience with the theorem and its proof. Eventually, ask the student to r ...
... Provide feedback to the student concerning any errors or omissions and allow the student to revise his or her proof. Consider implementing the MFAS task Justifying a Proof of the AA Similarity Theorem (G-SRT.1.3) for further experience with the theorem and its proof. Eventually, ask the student to r ...
Regional Integrated Geometry Curriculum
... G.G.11 Know and apply that two prisms have equal volumes if their bases have equal areas and their altitudes are equal G.G.12 Know and apply that the volume of a prism is the product of the area of the base and the altitude G.G.13 Apply the properties of a regular pyramid, including: lateral edges ...
... G.G.11 Know and apply that two prisms have equal volumes if their bases have equal areas and their altitudes are equal G.G.12 Know and apply that the volume of a prism is the product of the area of the base and the altitude G.G.13 Apply the properties of a regular pyramid, including: lateral edges ...
Keys GEO Openers 4-15
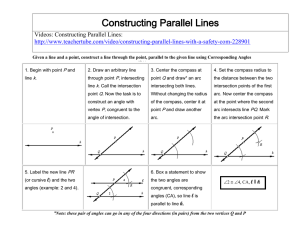
... If 2 lines are cut by a transversal so that each pair of CI s is supplementary, then the lines are ||. If 2 lines are cut by a transversal so that each pair of AI s is , then the lines are ||. If you have 1 line and 1 point NOT on that line, ONE and only ONE line goes through that point that’s || ...
... If 2 lines are cut by a transversal so that each pair of CI s is supplementary, then the lines are ||. If 2 lines are cut by a transversal so that each pair of AI s is , then the lines are ||. If you have 1 line and 1 point NOT on that line, ONE and only ONE line goes through that point that’s || ...
Name
... 7. The expressions (3x + 63)° and (7x – 45)° represent the measures of two angles of a regular decagon. Find the measure of an angle of the decagon. ...
... 7. The expressions (3x + 63)° and (7x – 45)° represent the measures of two angles of a regular decagon. Find the measure of an angle of the decagon. ...
MATH 131 Problem Set 5
... This problem set deals with the concurrence theorems for triangles. These theorems have a common format: given triangle ABC, then three lines, one associated with each vertex or with each side, are concurrent at a point, that is, all three of them pass through a certain point. Note: (November 20) In ...
... This problem set deals with the concurrence theorems for triangles. These theorems have a common format: given triangle ABC, then three lines, one associated with each vertex or with each side, are concurrent at a point, that is, all three of them pass through a certain point. Note: (November 20) In ...
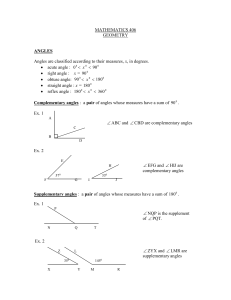
angles
... Parallelogram - a quadrilateral having two pairs of opposite sides parallel Square – a quadrilateral having four congruent sides and one right angle Rectangle – a parallelogram having one right angle Rhombus – a parallelogram having four congruent sides Trapezoid – a quadrilateral having a pair of o ...
... Parallelogram - a quadrilateral having two pairs of opposite sides parallel Square – a quadrilateral having four congruent sides and one right angle Rectangle – a parallelogram having one right angle Rhombus – a parallelogram having four congruent sides Trapezoid – a quadrilateral having a pair of o ...
DAY-4---Quadrialaterals-RM-10
... that any theorem proved from them was deemed true in an absolute, often metaphysical, sense. Today, however, much non-Euclidean geometry is known, the first ones having been discovered in the early 19th century. One important application of the notion of non-Euclidean geometry is Einstein's theory o ...
... that any theorem proved from them was deemed true in an absolute, often metaphysical, sense. Today, however, much non-Euclidean geometry is known, the first ones having been discovered in the early 19th century. One important application of the notion of non-Euclidean geometry is Einstein's theory o ...
Achieving the grade C in Maths
... move either left or right if it is positive it will move right and negative means left. Tells me how far it will move either up or down if it is positive it will move up and negative ...
... move either left or right if it is positive it will move right and negative means left. Tells me how far it will move either up or down if it is positive it will move up and negative ...