Download Achieving the grade C in Maths

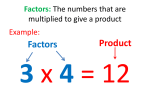
Top-Notch
Guide
To
Mathematics
Designed to improve the number of
students achieving grade C at GCSE
M.Woodfine
Don’t forget to use the website as well!
www.hinchingbrookeschool.net
When is a good time to revise? Definitely not when you have the T.V. on or when
you are bored! You won’t learn anything during this time! Make sure you dedicate
some time to revision. You tell yourself that during a particular time period you
will sit down and do nothing but revision. After you have done your revision make
sure you reward yourself! It is all about the sour and sweet! The sweet is only
better when you have suffered the sour!
Shape, Space And Measure
Measuring Angles:
3.
4.
2.
3.
1.
1. and 2.
1. Place the centre of the
protractor on the point
where the two lines meet.
2. Make sure 0 on the
protractor, lines up with one
of the lines.
3. Measure from where 0 is
(either on the inside or the
outside of your protractor)
to the angle. You should be
counting up from 0 to
measure your angle.
Area and perimeter of 2D
shapes:
Area is the space within a shape.
Perimeter is the distance all the
way round a shape.
Area of square or rectangle:
Base x height
1. Start with a straight line.
2. Make sure the centre of the
protractor is on the end of
the line.
3. Make sure 0 on the
protractor, lines up with the
straight line.
4. Measure from 0 to the
appropriate angle, mark the
angle from the protractor
with a dash.
5. Remove the protractor and
complete the angle with a
straight line from where the
centre was to the dash.
1. Always measure from the
north line.
2. Always measure the angle
in a clockwise direction.
3. Always write the angle as a
3 figure number, e.g. 60o
would be written as 060o.
Another thing to remember is
the wording in the question.
The bearing of B from A is 70o:
B
o
70
290o
A
Whereas the bearing of A from B
is 290o.
Area and circumference
of a circle:
Angles on a straight line add up
to 180o.
1.
3.
2.
Angles in any triangle add up to
180o.
h
The interior angle sum in any
polygon is based on how many
triangles it can be divided into:
Area of parallelogram:
Base x Height
h
A polygon is
a straight
sided shape
b
Area of triangle:
½ x Base x Height
½ x (a+b) x h
A bearing is the angle between
two points. There are 3 key
things to remember about
bearings:
Angles on a straight line and
interior angle sum:
b
Area of trapezium:
Bearing:
Drawing Angles:
h
b
a
h
b
1. Start at one corner and
draw a line to every other
corner.
2. Count how many triangles it
has been divided into and
then times it by 180.
3. In this case 4 x 180 = 720o
1. Radius – distance from the
centre to the outside of the
circle
2. Diameter – distance from
one side of the circle to the
other through the centre
3. Circumference – special
name for the perimeter of a
circle
Area =  x Radius2
A =  x r2
Circumference =  x diameter
C=xd
Where  can be found on your calculator
or estimated at 3.14
Shape, Space And Measure
Pythagoras’ Theorem and Trigonometry:
There are 3 main things you should remember about triangles:
1. Angles in any triangle add up to 180o.
2. Pythagoras’ Theorem; a2 + b2 = c2
3. Trigonometry; SOH CAH TOA
Pythagoras’ Theorem and Trigonometry only apply to right-angled triangles
Pythagoras’ Theorem
Trigonometry
If you remember:
c
a
You will remember everything you need to about
trigonometry.
The area of the two smaller squares (a and b) will
add up to the area of the larger square (c).
Adjacent
Area of A = a x a = a2
Area of B = b x b = b2
Area of C = c x c = c2
2
2
a +b =c
2
Things to remember:
 c is always the side opposite the right
angle!
 Only use Pythagoras when you know 2
sides and need to work out the third side.
To calculate the longer side (c):
3
4
We need to work out the side opposite
the right angle, we have been given 2
sides and it is a right angle triangle so we
can use Pythagoras’ Theorem.
1. Label the 2 shorter sides a and b.
2. a2 + b2 = c2
32 + 42 = c2
9 + 16 = c2
c2 = 25
3.
c2 = 25
c = 25
c=5
To calculate one of the shorter sides (a or b):
8
5
We need to work out a shorter side,
we have been given 2 sides and it is a
right angle triangle so we can use
Pythagoras’ Theorem.
?
1. Label the shorter side b and the side opposite
the right angle c.
2. a2 + b2 = c2
a2 + 52 = 82
a2 + 25 = 64
H
yp
ot
en
us
e

Opposite
b
?
SOH CAH TOA
3.
a2 + 25 = 64
-25
-25
a2
= 39
a = 39 = 6.244
Hypotenuse –
Always the side opposite to the
right angle.
Opposite –
Always the side opposite to the
angle ().
Adjacent –
Always the side next to the
angle ().
So what does it mean?
SOH
CAH
Sin  = Opposite
Hypotenuse
TOA
Cos  = Adjacent
Hypotenuse
Tan  = Opposite
Adjacent
You need to choose which of the three above you
should use depending on the problem. It all relates
to what information you have been given.
Working out one of the sides:
35o
?
5
We need to work out the side opposite
the right angle (hypotenuse), we have
been given the side opposite to the angle
(opposite) and the angle (). It is a right
angle triangle so we can use
Trigonometry.
List what we have been given:
Opposite, Hypotenuse and 
The only one that involves these 3 is SOH.
Sin  = Opposite
Hypotenuse
Sin 35 = 5
?
Rearrange the formula  ? =
5
= 8.717
Sin 35
Working out the angle ():
Imagine if we had been given:
Opposite = 5 and
Adjacent = 6
What would the angle () be?
The only one that involves these 2 is TOA.
Tan  = Opposite
Tan  = 5
Tan  = 0.8333
Adjacent
6
The opposite of Tan is Tan-1:
Tan-1 Tan = Tan-1 0.8333 = 39.8o
Shape, Space And Measure
Enlargement:
Enlargement is making a shape
either larger or smaller. It is
different to the original, only in
size. There are 3 important
things you need to remember
when enlarging a shape.
1.
2.
3.
Where is the centre of
enlargement? This is the point
where the distances to each corner
are altered according to the scale
factor.
Scale factor – this tells you how big
or small the shape will become.
Draw the rays as guidelines
through each corner from the
centre of enlargement.
Enlarge the following shape with a scale
factor of 2 with centre of enlargement
(1, 2):
When it is an enlargement by a scale factor
of 2, you double the distances from the
centre of enlargement to each corner. If it
had been an enlargement by a scale factor
of 3, you would times the distances by 3.
Centre of
enlargement
Translation:
Translation can be best
described as picking an object
up, moving it and placing it back
down without changing the
shape in anyway.
With translation, we are told
where a shape will move,
according to a particular vector:
x 
 y
 
Tells me how far it will
move either left or right
 if it is positive it will
move right and negative
means left.
Tells me how far it will
move either up or down
 if it is positive it will
move up and negative
means down.
3 
2
 
This means each point in the
shape will move 3 squares
right and 2 squares up
 5
  8
 
This means each point in the
shape will move 5 squares
left and 8 squares down
Rotation:
Reflection:
Just like when you look in the
mirror, you need to think about
3 things about your reflection:
1.
2.
3.
What is the original object?
Where is the mirror line?
How far is the object from the
mirror line because the reflected
image will be the same distance
away? The image will look similar
with the same properties as the
original except a reflection.
1.
2.
3.
Mirror Line
Object
Rotation can be best described
as twisting a shape around a
point. The shape does not alter
in anyway other than its position
and orientation. The rotated
shape will be the same distance
away from the centre of rotation
as what the original was. There
are 3 things to remember:
Image
Where is the centre of rotation?
Will it rotate clockwise or anticlockwise?
What is the angle that it will rotate
through?
Rotate the following shape around the
point (0, 0), 90o in a clockwise direction.
Object
Notice: Each point in the object
is the same distance away from
the mirror line as what they are
in the object. The object had 3
right angles, as does the image.
Construction:
For the exam, there are several
types of construction you will
need to become familiar with:
1. Constructing a triangle.
2. Constructing the
perpendicular bisector.
3. Constructing the angle
bisector.
These are best described on the
Mathematics website in the
video loci.
www.hernebayhigh.kent.sch.uk/maths
Centre of
rotation
Rotate the rays through 90o clockwise
and then measure the distances from
the centre of rotation
Loci:
When you are on a round-about
you will be moving in a circular
motion.
When you are on a big-wheel at
a fair you will be moving in a
circular motion.
When you are on a plane at
take-off, your movement will
look like this:
In order to score as many marks
as possible:
NEVER RUB OUT YOUR
CONSTRUCTION LINES
WITH ANY OF YOUR
DRAWINGS FOR ANY OF THE
TOPICS ON THIS PAGE!!!!
A locus is a set of points that
follow a particular rule or path.
The drawings above are
examples of loci as they follow
the particular rules or path
specified.
Question Time – Shape, Space And Measure
1.
20 cm
The diagram shows a shape.
Diagram NOT
accurately drawn
Work out the area of the
9 cm
shape.
4 cm
…………………………… cm2
8 cm
2.
(Total 4 marks)
The diameter of a circle is 12 centimetres.
(a)
Diagram NOT
drawn accurately
12 cm
Work out the circumference of the circle.
Give your answer, in centimetres, correct to 1 d.p.
.............................. cm
(2)
Diagram NOT
accurately drawn
The length of each diagonal of a square is 20 cm.
(b)
Work out the area of the square.
.............................. cm2
(2)
(Total 4 marks)
y
5
3.
4
3
A
2
1
–5
–4
–3
–2
–1 O
1
2
3
4
5
x
–1
–2
–3
–4
–5
(a)
(b)
On the grid, rotate triangle A 180° about O.
Label your new triangle B.
On the grid, enlarge triangle A by scale factor
Label your new triangle C.
(2)
1
, centre O.
2
(3)
(Total 5 marks)
Algebra
Simplifying:
When we simplify an expression,
we collect together only like
terms (in other words, only the
things that have something in
common, i.e. the same letter):
a+a+a+b+b
would be simplified to:
3a + 2b
3a + a + 4b + 2a +b
would be simplified to:
6a + 5b
5a2 + 6b + 8a + 2a2
would be simplified to:
7a2 + 8a + 6b
2
a is as different to a, as a is to b
Note the clear difference
between a2 and a. The
difference can be shown with
the next example; showing the
difference between a6 and 6a
If we had:
a5 x a3
What would this mean?
Write in long form:
(a x a x a x a x a) x (a x a x a)
In other words:
axaxaxaxaxaxaxa
We have the same letter/number
multiplied together; we use
indices to write it more easily:
a8
5
Thing to remember when
multiplying an algebraic
expression is to group the
numbers together and then the
letters; then simplify:
e.g. 5a x 6b x 3a
means:
5xax6xbx3xa
becomes: 5 x 6 x 3 x a x b x a
becomes: 30 x 3 x a x a x b
becomes: 90 x a x a x b
90a2 x b = 90a2b
8
There are some other laws that
are useful to remember:
xa x xb = xa+b
a
b
x ÷x =x
a-b
Substitution works in exactly the
same way in Mathematics as it
does in football or netball. You
replace something in exactly the
same position. In Maths, a letter
is replaced by a number.
Substitute n = 4 into the
following expressions:
a) 6n
b) n2
i) What does 6n mean?
Remember 6n means 6 x n so we
need to replace n with 4.
ii)
6xn
6 x 4 = 24
What does n2 mean?
Remember n2 means n x n so now
swap n for 4.
nxn
4 x 4 = 16
Substitute p = 3 and r = 2 into
the following expression:
p3 + 4r
Write down what p3 and 4r mean
(xa)b= xaxb
pxpxp+4xr
3 x 3 x 3 + 4 x 2 = 27 + 8
= 35
Expanding and factorizing:
Let’s make it harder!
When we multiply anything it
does not matter about the order
that we do it in. So we can
rearrange this expression:
5a x 2a
means:
5xax2xa
becomes: 5 x 2 x a x a
becomes: 10 x a x a
becomes: 10 x a2
10a2
3
Notice the pattern: a x a = a
We simply added the powers!
a6 = a x a x a x a x a x a
6a = 6 x a = a + a + a + a + a + a
What if we had:
5a x 2a
Substitution:
Index laws:
Expand means to make bigger.
So with this example: 3(x + 5)
means get rid of the brackets.
Everything on the inside of the bracket, needs multiplying by that on the outside.
3x
3(x + 5) = 3x + 15
+15
There are 2 other examples that you might encounter in an exam:
a) 2(x – 3) + 6(x +8)
b) (x + 3)(x – 1)
Remember everything on the inside needs multiplying by that on the outside
2x
a) 2(x – 3) + 6(x +8)
-6
=
=
-1x
6x
+48
2x + 6x -6 + 48
8x + 42
b)
2
x
(x + 3)(x – 1)
3x
-3
= x2 – 1x + 3x – 3
= x2 + 2x - 3
Factorizing is the opposite of expanding.
We need to place in brackets. This is done by looking for the connection between the
numbers/ letters in an expression. It is the connecting letter and/or number that
then goes on the outside of the bracket.
4x + 24
2x2 + 10x
Connection 4, this goes on outside
4(x + 6)
Connection 2 and x, this goes on outside 2x(x +5)
Algebra
Co-ordinates:
A co-ordinate is based on 2
numbers (x, y). We need the
two points in order to position a
cross on a graph. To find these
numbers it is all based on
substitution and a rule.
E.g.
y = 3x – 2
This tells me that y is 3 times
what x is, minus 2.
x
y
-1
0
1
2
Find y by substituting in
x = -1, x = 0, x = 1 and x = 2
into our rule of y = 3x – 2.
Changing the subject of a
formula is like solving an
equation, only difference is we
are not aiming to find a value of
a letter. We re-arrange a formula
so as to trade letters. Take the
following for example, but also
read how to solve a linear
equation:
0
-2
1
1
5 , 8 , 11 , 14 , 17 , …
It goes up by 3’s, it’s then based on the
3 times table. What do we need to do to
the times table? Write the times table
above the sequence, so we can see:
+2
Therefore, the rule is
Times table
So this means changing from y=
to x=.
y = 4x + 3
-3
-3
y – 3 = 4x
2
4
Therefore the points to plot are:
(-1, -5) , (0, -2) , (1, 1) , (2, 4)
÷4
÷4
3 , 6 , 9 , 12 , 15 , …
5 , 8 , 11 , 14 , 17 , …
Notice we need to add 2 to each of the 3
times table numbers.
y = 4x + 3
Do the same for the other values of x.
-1
-5
Finding the rule:
Change the subject from y to x.
First of all, substitute x = -1:
y = 3 x -1 – 2
y = -5
x
y
Nth term of linear equations:
Changing the subject:
3n + 2
What we do to it
Use a rule to generate a
sequence:
5n – 2
It is based on the 5 times table. Write
this down. It then says you need to take
2 from each number.
4x = 4 x x
Opposite of x4
is ÷4
x=y–3
4
-2
5 , 10 , 15 , 20 , 25 , …
3 , 8 , 13 , 18 , 23 , …
Find the 50th term:
Using the rule 5n – 2 as an example,
substitute n = 50 into the rule to find the
50th term:
5 x 50 – 2 = 250 – 2 = 248
Solving linear equations:
Simultaneous equations:
When solving an equation, always look to simplify
the problem first by collecting like terms or
expanding brackets.
By definition, simultaneous means operating at
the same time. Simultaneous equations means
solving 2 equations at the same time to work out
2 different values.
Solving equations:
5x – 4 = 26
5x – 4 = 26
+4 +4
1.
2.
Get rid of what you are adding or
subtracting by doing the opposite
5x
÷5
= 30
÷5
5x is short for 5 x x
Opposite of x5 is ÷5
x
=6
We have now eliminated all
numbers from the side with x on it
Expanding:
3(x + 6)
3x + 18
-18
3x
÷3
x
= 24
= 24
-18
=6
÷3
First thing to do is to look for a connection between the 2
equations. Notice both have 2y in them. We can then
eliminate y by taking equation 2 away from equation 1:
2x
Collecting like terms (unknowns on both sides):
8x + 4 = 3x + 49 Remove the smaller number of x’s
-3x
-3x
first then follow usual steps
5x + 4 =
49
=8
Solve by dividing both sides by 2 gives x = 8. Substitute this
value of x into equation 1 and then solve to find y:
5x + 2y = 8
5 x 8 + 2y = 8
40 + 2y = 8
2y = -32
y = -16
Expand then follow the previous
steps
=2
5x + 2y = 16
3x + 2y = 8
Substitution of x = 8
Solve using the usual
steps as this is a
linear equation now
What if the equations haven’t anything in common at start?
1.
2.
5p + 4q = 22
3p + 5q = 21
Notice how 4q and 5q could both go into 20q. That would
mean we need 5 lots of equation 1 and 4 lots of equation 2 to
give 20q in each. We can then eliminate q by doing equation
1 take away equation 2:
25p + 20q = 110
12p + 20q = 84
Question Time – Algebra
1.
(a)
Simplify
(i)
3g + 5g
.................................
(ii)
2r × 5p
.................................
(2)
.................................
(1)
5(2y – 3)
(b)
Expand
(c)
Expand and simplify
2(3x + 4) – 3(4x – 5)
.................................
(2)
(Total 5 marks)
2.
(a)
Factorise 3t – 12
.................................
(b)
Expand and simplify 3(2x – 1) – 2(2x – 3)
.................................
(1)
(2)
(Total 3 marks)
3.
A straight line has equation y = 4x – 5.
(a)
(b)
Find the value of x when y = 1.
x = .................................
(2)
Rearrange the equation y = 4x – 5 to find x in terms of y.
x = .................................
(2)
(Total 4 marks)
4.
(a)
Work out the value of 3p + 4q when p = 5 and q = –2
(b)
.................................
Given that y = 4x – 3, work out the value of x when y = 11
x = .................................
(2)
(3)
(Total 5 marks)
5.
On the grid, draw the graph of y = 2x – 3
Use values of x from x = –1 to x = 4
6.
(Total 3 marks)
The first term of a sequence is 7. The rule for the sequence is Add 5 to the previous term.
(a)
Write down the second term and the third term of the sequence.
....……… , ……………
(b)
Work out the 10th term of the sequence.
.................................
(c)
Write down an expression, in terms of n, for the nth term of the sequence.
.................................
7.
(1)
(2)
(2)
(Total 5 marks)
Solve the simultaneous equations
2x + 3y = 6
3x − 2y = 22
x = ……………………
y = ……………………
(Total 4 marks)
Number
Conversion between fractions,
decimals and percentages:
Divide the
numerator by
the denominator
Equivalent in Mathematics
means to have the same value.
x 100
Fractions Decimals Percentage
÷ 100
Read the place
value
Fraction  Decimal:
Use short division to divide the
numerator by the denominator:
5
6
5 = 0.833
6
Decimal  Fraction:
Read the place value of the last digit in
the decimal. 0.024, the 4 is in the
thousandths column, so write 24 over
thousand and then simplify down.
So,
0.5 = ½ = 50%
These are all equivalent because
they have the same value, they
are just written as a decimal,
fraction and a percentage.
We can write fractions with the
same value by writing them as
equivalent fractions. This is done
by multiplying or dividing both
the numerator and denominator
by the same number. This is
essential when we simplify or
write an equivalent fraction.
WHAT EVER YOU DO TO THE
TOP, YOU DO TO THE BOTTOM!
Decimal  %  Decimal:
8
16
When we multiply by 100 we move the
decimal point 2 places to the right. When
we divide by 100 we move the decimal
point 2 places to the left.
Fractional part of a quantity:
Divide the number by the
denominator and then multiply
by the numerator.
By doing this you are finding
what 1 part is and then
multiplying by how many there
are:
13 of 75
15
So 13 of 75 = 13 x ( 1 of 75)
15
15
= 13 x 5 = 65
Equivalent fraction
See if the fraction can be written as an
equivalent fraction with a denominator of
100. That then makes the above process
easier as we know how to divide by 100.
10 of 30
25

40 of 30
100
0.27 , 6 , 56% , 9 , 0.82
7
10
First convert them all into decimals
using the information on this page:
Ordering decimals:
0.27 , 0.857 , 0.56 , 0.9 , 0.82
Place in the correct place value column
U.
0.
0.
0.
0.
0.
th hth Thth
2 7
8 5
7
5 6
9
8 2
Don’t forget to place the numbers back
into context according to the question.
Turn all fractions into equivalent
fractions with a common denominator.
Ratio:
A ratio is different to a fraction.
Work out what the value of
10%, 5% and 1% and see what
combination will make the
percentage of 13%.
100% of 65 = 65
10% of 65 = 6.5
÷2
÷ 10
÷2
5% of 65 = 3.25
÷ 10
A fraction tells you what you have out of
a total, like a test score or probability.
A ratio compares 2 numbers like the
amount of money I have compared to
that of a friend.
E.g.
Amount I have : Amount he has
£120 : £180
Ratio can be simplified in a similar way to
a fraction (what ever you do to one side
you do to the other):
1% of 65 = 0.65
To get 10% divide 100% by 10
To get 5% divide 10% by 2
To get 1% divide 10% by 10
So to make 13%, all we need is
10% and 3 lots of the 1%
10% + 3 x 1%
6.5 + 3 x 0.65 = 8.45
Alternative method:
13% of £65
could be
written as
Start from the left,
find the smallest
value first by looking
at each column:
0.27, 0.56, 0.82,
0.857, 0.9
0.27 , 56% , 0.82 , 6 , 9
7 10
Ordering fractions:
1
2
13% of £65
÷ 10
of 75 = 75 ÷15 = 5
÷8
=
÷8
There are many different
applications of when you might
need to order numbers. The
worst type you might encounter
is when you have a mixture like:
Percentage part of a quantity:
÷ 10
E.g.
1
15
Ordering:
Equivalences:
13 of 65
100
So then solve it as a fraction problem
£120 : £180
£12 : £18
£6 : £9
£2 : £3
Means for every £2 I have, he has £3
Dividing an amount according to a ratio
Divide £30 into the ratio 4:6
This will then be divided so 4 parts go to
me, 6 parts to him with 10 parts in total.
1 part = £30 ÷ 10 = £3
If I get 4 parts then 4 x £3 = £12
If he gets 6 parts then 6 x £3 = £18
Money is split
£12 : £18
Checking procedure: Add
numbers in ratio to check if
they equal original amount
Number
BIDMAS and estimation:
We need a set of rules that
enables everyone to get exactly
the same answer. This is where
BIDMAS comes into play.
BIDMAS tells you to what to look
out for first in a calculation.
B
I
D
M
A
S
rackets
ndices (powers)
ivision
Look for these
ultiplication
in the order that
they appear,
ddition
from left to right
ubtraction
3.1 + 5.38 x 2.9
6.1
Multiplying by a decimal:
We don’t have a sensible way of
multiplying decimals; in fact you
probably have never been told
how to do it. We only know how
to multiply whole numbers, so
with decimals we make the
problem easier. Multiply each
decimal by a power of 10 to
make them whole numbers:
0.48 x 0.5
x 100
48
Always estimate an answer. Estimation is
like best guess. Round each number
3+5x3
6
Apply BIDMAS  multiplication first 
then addition  division
3 + 15 = 18 = 3
6
6
Now work out the answer, you should
find out that it is close to 3.
3.1 + 15.602 = 18.702 = 3.066
6.1
6.1
Negative numbers:
Remember this:
WHEN THE SIGNS ARE THE
SAME IT IS A GOOD THING
(POSITIVE)
WHEN THE SIGNS ARE
DIFFERENT IT IS A BAD THING
(NEGATIVE)
x 10
x
5
The answer to 0.48 x 0.5 is not 240. You
must remember we altered the problem
to start with by x100 and also x10. We
need to put the problem back into
proportion by doing the opposite.
240
÷ 10
2.4
0.24
Rounding to a certain number of
significant figures or decimal
places:
When we round to a significant
figure (s.f.) or decimal place
(d.p.), it’s based on:
Look next door, if it’s 5 or more
at 1, if it’s less than 5 leave it,
numbers to the right go to 0.
This works in the following cases:
Significant figures:
Multiplying and dividing:
Significant figure means most important.
So if we round to 2 significant figures,
we need the 2 most important and the
rest turn to 0.
Round 9432.223 to 2 s.f.
-3 x -4 = 12
(positive because the signs
are the same)
-5 x 2 = -10
(negative because the signs
are different)
-60 ÷ 5 = -12
(negative because the
signs are different)
Adding and subtracting:
If there are 2 signs next to one another
we need to replace them with just one.
8-+2=6
(change to a minus because
the signs are different)
8 - - 2 = 10
(change to a plus because
the signs are the same)
+
9432.223
Circle the 2nd most important number.
Look next door and apply the principle.
This is then rounded to:
9400
Decimal places:
Round the same number to 2 d.p. Circle
the second number after the decimal
point and then apply the principle.
9432.22
5.35 ÷ 0.5
This can also be written as:
5.35
0.5
Since when have we had
decimals in a fraction. Convert
the fraction into an equivalent
fraction by multiplying the
numerator and denominator by
100.
5.35 =
0.5
48 x 5 = 240
÷ 100
Dividing by a decimal:
535
50
Now we can do 535 ÷ 50
0 1 0 . 7
50 55 335 .350
And because we converted the
division problem into an
equivalent fraction 5.35 ÷ 0.5
has the same value as 535 ÷ 50
Differences between time:
When we are trying to find out
the difference between two
times, always count up in small
increments. Count up to the
nearest hour then take
reasonable steps.
Question:
I leave at 8.15am and arrive at
1.21pm. How long was my
journey?
45mins
3hr
1hr
21mins
8.159.0012.001.001.21
Then count up all the minutes
and hours.
45mins + 3 hrs + 1 hr + 21mins
= 4hrs + 45mins + 21mins
= 4hrs + 66mins
= 5hrs 6mins
Number
Adding and subtracting fractions:
When we have two fractions that are either added or subtracted with
a common denominator, we add or subtract the numerators and
keep the denominator the same:
More complex addition and
subtraction of fractions:
What if we had a more
complicated problem such as:
3 2 5
 
7 7 7
5
3
3 2
6
8
What do we need to do if the fractions do not have a common
denominator? Take the following for example:
We solve it in a very similar way
but first split the whole numbers
and fractions up, solving
separately.
5 3

6 8
We need to turn these fractions into equivalent fractions that have
the same denominator. 6 and 8 both go into 24, so we need to write
these fractions with the common denominator of 24:
5 20

6 24
and
3 9

therefore the problem now becomes
8 24
20 9 29


24 24 24
But we have a top heavy fraction. To turn it into a mixed number,
see how many times the denominator goes into the numerator and
write the remainder over the same denominator.
29
5
1
24
24
24 goes into 29 once with a remainder of 5
20 9 11


24 24 24
3–2=1
We now bring the 2 answers
together (both the whole
number and the fraction) to
give:
1
11
24
So, break the mixed numbers
apart, solve separately and then
bring the 2 individual answers
together again.
Multiplying fractions:
Dividing Fractions:
There is just one key thing to remember 
Multiply the numerators together, multiply the
denominators together and then simplify!!
Flip the second fraction and the division
problem turns into a multiplication problem.
4 3 12
 
7 8 56
simplified to

3
14
What do we do if we have:
4 2 4 2 8
1
 
 1
7 1 7 1 7
7
5
3
3 2
6
8
I always say convert both fractions into top
heavy fractions first. If I have:
5
3
6
it means I have 3 whole and
5
6
To convert into a top heavy fraction, multiply
the number in front of the fraction by the
denominator and add it to the numerator, e.g.
3 x 6 + 5 = 23
Therefore the first fraction becomes:
23
6
3
, problem becomes:
8
23 19 437
5
 
9
6 8
48
48
Do the same to
2
4 1

7 2
What if we had the following problem:
6
2
3
Any whole number can be written over 1.
Therefore, the problem can be written as
followed and solved by flipping the second
fraction (ANY whole number can be written
over 1!!!):
6 2 6 3 18
   
9
1 3 1 2 2
Remember: if we have mixed numbers and they
are either multiplied or divided, turn them into
top heavy fractions first.
Question Time – Number
1.
(a)
Estimate the value of
68  401
198
..........................
(2)
(Total 2 marks)
2.
(a)
Write the number 56 392 correct to one significant figure.
.............................
(1)
(b)
Write the number 0.0436 correct to one significant figure.
.............................
(1)
(Total 2 marks)
3.
The cost of 4 kg of apples is £3.36. The total cost of 3 kg of apples and 2.5 kg of pears is
£4.12
Work out the cost of 1 kg of pears. Give your answer in pence. .......................... p
(Total 3 marks)
4.
2 3

5 8
(a)
Work out
(b)
Work out 5 23 – 2 34
……………………… (2)
……………………… (3)
(Total 5 marks)
5.
Write these numbers in order of size.
Start with the smallest number.
7
3
35%
(i) 0.4
........................................................................................................
7
15
(ii)
5, – 6, – 10, 2, – 4
...............................................................................................
(iii)
1 2 2 3
, , ,
2 3 5 4
................................................................................................
(Total 5 marks)
6.
A customer who cancels a holiday with Funtours has to pay a cancellation charge.
The cancellation charge depends on the number of days before the departure date the customer
cancels the holiday. The cancellation charge is a percentage of the cost of the holiday. The
table shows the percentages.
The cost of Amy’s holiday was £840.
She cancelled her holiday 25 days before
the departure date.
(a)
Work out the cancellation charge
she had to pay. £………
(2)
The cost of Carol’s holiday was £600.
She cancelled her holiday and had to pay
a cancellation charge of £480.
(b)
Work out £480 as a percentage of £600.
Number of days before the
departure date the customer
cancels the holiday
Percentage of the
cost of the holiday
29–55
40%
22–28
60%
15–21
80%
4–14
90%
3 or less
100%
…………………………. %
(2)
Ravi cancelled his holiday 30 days before the departure date. He had to pay a cancellation
charge of £272.
(c)
Work out the cost of his holiday.
£ ……………………………
(2)
(Total 6 marks)
Handling Data
MMMR:
Stem and leaf diagram:
Frequency table:
There are 3 different types of
average; mean, mode, median.
Mode
In French, mode means most
fashionable. In maths it means
the most common.
Median
Median sounds like medium
which means the middle. To find
the median we put the numbers
into size order then find the
middle one. If there are two
middle numbers find the mean
of these two values.
Hint: to find the middle value cross out
the smallest, then the largest, then the
smallest and so on. This will help you to
find it without any mistakes.
Mean
Add them all together and then
divide by how many there are.
Range
Difference between the highest
and the smallest value:
Highest value – lowest value
By definition, frequency means
how many times something
occurred or appeared.
A frequency table is an easy way
of displaying simple data.
Frequency is often used to count
how many data values have
been marked in a tally chart:
Colour
Red
Blue
Green
Yellow
Tally
III
IIII III
I
IIII IIII
Frequency
3
8
1
10
The frequency column was filled
in by counting how many marks
there were in the tally column.
In this case, yellow was the
most favourite colour and green
was the least favourite.
When collecting data, it is
sometimes hard to observe and
record at the same time. This is
where stem and leaf diagrams
are useful. After it has been
produced, you only need to
record half the data.
E.g. A survey was taken to see how
much people would be willing to spend
on a slice of bread. The following stem
and leaf diagram was produced.
4
3
2
1
0
0
1
2
6
5
8
2
4
8
9
3
7
5
8
6
7
9
Importance of a stem and leaf
diagram is the key:
3 4 means 34p
4 5 means 45p
Having a table like this, you
only need to record the pennies
in the relevant row, i.e.
1?p, 2?p, 3?p or 4?p
How to calculate the mode, mean and median from a frequency table:
Calculating MMM from a frequency table
Calculating MMM from a grouped interval table
19 Yr 7 students were asked about their weekly pocket money:
31 students were asked about how long it takes to get to work:
Amount
50p
£1
£2
£5
Tally
IIII III
IIII
III
III
Frequency
8
5
3
3
Time
0< t ≤5
5< t ≤10
10< t ≤15
15< t ≤20
Frequency
3
16
8
4
Mode
The one that appears the most often  50p
Mode
The one that appears the most often  5< t ≤10
Median
The middle value when they are all in order. The table means:
Median
The middle value when they are all in order.
50p appeared 8 times, £1 appeared 5 times, £2 appeared 3
times and £5 appeared 2 times
In otherwords 50p, 50p, 50p, 50p, 50p, 50p, 50p, 50p, 50p,
…… which would take along time to list if I had asked 200
students to take part in my survey.
To find the middle value add one to how many were in the
survey and then divide by 2  19 + 1 = 10th student I need.
2
There were 8 students in the survey who said they got 50p
then 5 students who said they got £1. That makes the total 15
students in the first 2 categories; so the 10th student lies in the
2nd category (£1), i.e. the median is therefore £1.
Mean
At the moment there are 8 lots of 50p = £4, 5 lots of £1 = £5,
3 lots of £2 = £6 and 3 lots of £5 = £15. Therefore the total is
£4 + £5 + £6 + £15 = £30. You could use the last column for
the multiplications. The mean is calculated by dividing the total
by how many there are  £30 / 19 = £1.56
To find the middle value add one to how many were in the
survey and then divide by 2  31 + 1 = 16th student I need.
2
16th value lies in the 5< t ≤10 category.
Mean
Use the middle column to fill in the midpoint of each interval.
Time
0< t ≤5
5< t ≤10
10< t ≤15
15< t ≤20
3 lots of 2.5 = 7.5
16 lots of 7.5 = 120
8 lots of 12.5 = 100
4 lots of 17.5 = 70
Midpoint
2.5
7.5
12.5
17.5
Frequency
3
16
8
4
Add them all together and divide
by how many there are.
Mean = 7.5 + 120 + 100 + 17.5
30
= 297.5 = 9.92
30
Handling Data




A suitable question for the
questionnaire must be asked that
relates to the question in the exam
(i.e. in this case a restaurant)
What do you think you would want
to know from giving someone the
questionnaire? (what type of
restaurant they like, favourite food,
etc)
How are the people going to
respond in the question? (multiple
choice, etc)
If you give times in a multiple
choice question, make sure that in
the options given, you don’t
overlap, e.g. 0-5 hours
5-10 hours
What option would you tick if you
worked for 5 hours?
Probability of a single event:
The probability is a value to
represent the likelihood of an
event happening. Probability is
measured between 0 and 1
(where 0 is impossible and 1 is
certain for it to happen).
Probability is calculated by
considering how many times an
event can happen out of how
many possible times that it could
appear.
Try to remember the easiest
example, what is the probability
of getting an even on a dice?
There are 3 even numbers on a
dice out of 6 possible numbers.
Therefore:
3 1

6 2
We need to divide the frequency by the
total frequency, then times it by 360.
This works out the fraction represented
by each category on a pie chart.
Job
Freq
Teacher
2
Plumber
3
Driver
12
Electrician
18
Doctor
6
Dentist
Researcher
Total
1
3
Angle
2
 360  16
45
3
 360  24
45
12
 360  96
45
18
 360  144
45
6
 360  48
45
1
 360  8
45
3
 360  24
45
A line of best fit and comments
on correlation apply to scatter
diagrams. A line of best fit is a
straight line that goes through
the middle of as many points as
possible to generalise the
pattern of the data points.
Below are the different types of
correlation with an example of a line of
best fit for each:
Weight vs Height
220
200
Positive
Correlation
180
Height
For example:
Mr Beeton is opening a restaurant.
He wants to know what type of
restaurant people like.
He designs a questionnaire.
We know in a circle there is 360o
Line of best fit and correlation:
160
140
120
100
50
55
60
65
70
75
80
85
90
Weight
Weight vs Height
220
200
Negative
Correlation
180
160
140
120
45
100
50
55
60
65
70
75
80
85
90
Weight
Weight vs Height
Construct a pie using a
protractor to accurately measure
each angle.
220
200
No
Correlation
180
Height
What makes a good survey
question? Here are some simple
rules you should follow in order
to be awarded with all the marks
in an exam:
Pie Charts:
Height
Survey questions:
160
140
120
100
50
55
60
65
70
75
80
85
90
Weight
Probability of multiple events:
When working out the
probability of more than one
event happening, you need to be
careful of the wording:
OR (+)
OR means add in probability.
What is the probability of getting a Jack
OR a Queen in a pack of cards?
P(Jack)= 4
52
P(Queen)= 4
52
P(Jack) or P(Queen)
4 + 4 = 8 = 2
13
52
52
52
AND (x)
AND means multiply in
probability.
What is the probability of getting a Jack
AND a Queen in a pack of cards?
P(Jack)= 4
52
P(Queen)= 4
52
P(Jack) and P(Queen)
4 x 4 = 16 = 1
2704
52
52
169
Using probability to work out
how many times something will
occur:
Sometimes you might know the
probability of an event
happening in theory, but what is
the likelihood of it happening
again.
There are 5 blue, 6 green and 4
yellow balls in a bag.
a) What is the P(blue)?
b) How many times will a blue appear if I
pull out 45 balls from the bag, replacing
each one after it has been picked out?
a) 5 = 1
15
3
b) If a blue appears one third of
the time, then if I pull out 45
balls from the bag, then:
1 of 45 = 1 x 45 = 15 blues
3
3
Question Time – Handling Data
1.
Anil counted the number of letters in each of 30 sentences in a newspaper.
Anil showed his results in a stem and leaf diagram.
Key
4 1
stands for 41 letters
0 8 8 9
(a)
1 1 2 3 4 4 8 9
2 0 3 5 5 7 7 8
3 2 2 3 3 6 6 8 8
(b)
4 1 2 3 3 5
(c)
Write down the number of sentences with 36
letters.
..............................
Work out the range.
..............................
Work out the median.
..............................
(1)
(1)
(1)
(Total 3 marks)
2.
The table shows information about the number of hours that 120 children used a computer last
week.
Number of hours
(h)
Frequency
0<h≤2
10
2<h≤4
15
4<h≤6
30
6<h≤8
35
8 < h ≤ 10
25
10 < h ≤ 12
5
Work out an estimate for the mean number of
hours that the children used a computer.
Give your answer correct to 2 decimal places.
……………… hours
(Total 4 marks)
3.
4.
Rosie had 10 boxes of drawing pins. She counted the number of drawing pins in each box.
The table gives information about her results.
Number of
drawing pins
Frequency
29
2
30
5
31
2
32
1
Work out the mean number
of drawing pins in a box.
.................................
(Total 3 marks)
A bag contains 6 red disks, 4 blue disks and 5 green disks.
A fair dice has 4 faces painted red and the other 2 faces painted blue.
Lisa takes a disk at random from the bag and records its colour.
Lisa then throws the dice twice and each time records the colour of the face it lands on.
Work out the probability that, of the three colours Lisa records, exactly two are the same.
………………………
(Total 5 marks)
5.
Mr Smith is going to sell drinks on his coaches.
He wants to know what type of drinks people like. He designs a questionnaire.
Design a suitable questionnaire, which he could use to find out what type of drink people like.
(Total 2 marks)