III. Quantum Model of the Atom
... C. Quantum Numbers Pauli Exclusion Principle No two electrons in an atom can have the same 4 quantum numbers. Each e- has a unique “address”: ...
... C. Quantum Numbers Pauli Exclusion Principle No two electrons in an atom can have the same 4 quantum numbers. Each e- has a unique “address”: ...
Presentation453.22
... As the quantum number gets larger, the probability increases towards larger displacement values. This corresponds to a classical phenomenon, as the energy of an oscillator increases, motion becomes more extended away from the status of lowest energy. The fundamental frequency of the oscillator is al ...
... As the quantum number gets larger, the probability increases towards larger displacement values. This corresponds to a classical phenomenon, as the energy of an oscillator increases, motion becomes more extended away from the status of lowest energy. The fundamental frequency of the oscillator is al ...
L 35 Modern Physics [1]
... to how fast the particle can go • According to Einstein, nothing can be accelerated to a speed greater than the speed of light, 186,000 miles per second ...
... to how fast the particle can go • According to Einstein, nothing can be accelerated to a speed greater than the speed of light, 186,000 miles per second ...
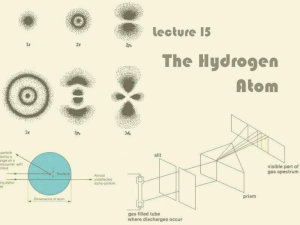
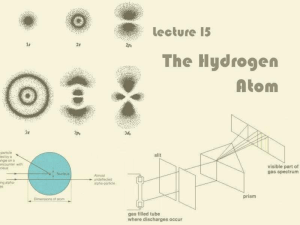
Lecture 15: The Hydrogen Atom
... Depending on which energy level it is in, the electron can take one of a number of stationary probability ...
... Depending on which energy level it is in, the electron can take one of a number of stationary probability ...
May 2001
... M01E.2—Radio Waves in a Gas of Charged Particles Problem In this problem, we investigate the effect of electromagnetic waves traveling through a gas of charged particles. This can happen when there is radio emission from a pulsar, and these signals propagate through clouds of charged particles in de ...
... M01E.2—Radio Waves in a Gas of Charged Particles Problem In this problem, we investigate the effect of electromagnetic waves traveling through a gas of charged particles. This can happen when there is radio emission from a pulsar, and these signals propagate through clouds of charged particles in de ...
Dr David M. Benoit (david.benoit@uni
... • This means that the measurement of property A can only result in one of its eigenvalues - even if the wave function is not an eigenfunction of ...
... • This means that the measurement of property A can only result in one of its eigenvalues - even if the wave function is not an eigenfunction of ...
Lecture 15: The Hydrogen Atom
... Electron does not fly round the nucleus like the Earth around the Sun (Rutherford, Bohr) Depending on which energy level it is in, the electron can take one of a number of stationary probability ...
... Electron does not fly round the nucleus like the Earth around the Sun (Rutherford, Bohr) Depending on which energy level it is in, the electron can take one of a number of stationary probability ...
The (Integer) Quantum Hall Effect
... One would expect, naively, that placing many charges (say, electrons) in a metal would cause them to interact very strongly through the Coulomb force, and that the resulting energy eigenstates would look very different from the single-particle energy eigenstates. Landau showed the remarkable result ...
... One would expect, naively, that placing many charges (say, electrons) in a metal would cause them to interact very strongly through the Coulomb force, and that the resulting energy eigenstates would look very different from the single-particle energy eigenstates. Landau showed the remarkable result ...
Aug 31 - BYU Physics and Astronomy
... Can stay normalized in time? If satisfies the Schrödinger equation and is normalizable, then indeed ...
... Can stay normalized in time? If satisfies the Schrödinger equation and is normalizable, then indeed ...
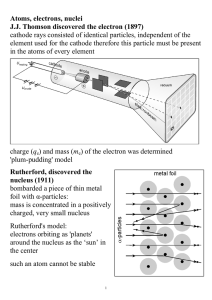
Electrons in Atoms
... that since we don’t know where exactly an electron is at any given moment, it is actually in all possible states simultaneously, as long as we don't look to check. It is the measurement itself that causes the object to be limited to a single possibility. ...
... that since we don’t know where exactly an electron is at any given moment, it is actually in all possible states simultaneously, as long as we don't look to check. It is the measurement itself that causes the object to be limited to a single possibility. ...
Quantum and Kala
... locate underground water sources and lost objects. Kala underlies the shaman’s awareness that all is alive, aware and responsive. Quantum physics laboratory demonstrations substantiate the Kala concept. Because of our Western scientific diehard fixation on objective reality perception, physicists ar ...
... locate underground water sources and lost objects. Kala underlies the shaman’s awareness that all is alive, aware and responsive. Quantum physics laboratory demonstrations substantiate the Kala concept. Because of our Western scientific diehard fixation on objective reality perception, physicists ar ...
B.R. Martin. Nuclear and Particle Physics. Appendix A. Some results
... dinstanced from each other by (π/L): (L/π)3 Or in the Fermi sphere it will be 1/8 of the sphere (because nxyz>0) n(k0)=1/8 ּ4/3πk03 ּ(L/π)3=V/(2π)3ּ4/3 πk03 - for all k
... dinstanced from each other by (π/L): (L/π)3 Or in the Fermi sphere it will be 1/8 of the sphere (because nxyz>0) n(k0)=1/8 ּ4/3πk03 ּ(L/π)3=V/(2π)3ּ4/3 πk03 - for all k
Particle in a box

In quantum mechanics, the particle in a box model (also known as the infinite potential well or the infinite square well) describes a particle free to move in a small space surrounded by impenetrable barriers. The model is mainly used as a hypothetical example to illustrate the differences between classical and quantum systems. In classical systems, for example a ball trapped inside a large box, the particle can move at any speed within the box and it is no more likely to be found at one position than another. However, when the well becomes very narrow (on the scale of a few nanometers), quantum effects become important. The particle may only occupy certain positive energy levels. Likewise, it can never have zero energy, meaning that the particle can never ""sit still"". Additionally, it is more likely to be found at certain positions than at others, depending on its energy level. The particle may never be detected at certain positions, known as spatial nodes.The particle in a box model provides one of the very few problems in quantum mechanics which can be solved analytically, without approximations. This means that the observable properties of the particle (such as its energy and position) are related to the mass of the particle and the width of the well by simple mathematical expressions. Due to its simplicity, the model allows insight into quantum effects without the need for complicated mathematics. It is one of the first quantum mechanics problems taught in undergraduate physics courses, and it is commonly used as an approximation for more complicated quantum systems.


![L 35 Modern Physics [1]](http://s1.studyres.com/store/data/008517000_1-9aef89c0ca089782f518550164188024-300x300.png)