Quantum Physics 2005 Notes-6 Solving the Time Independent Schrodinger Equation
... Letting z = x / L and scaling % =E / E0 and W = V / E0 we have: ...
... Letting z = x / L and scaling % =E / E0 and W = V / E0 we have: ...
30-32: Main Topics
... • involves 4 quantum numbers (3 more than the Bohr model) • quantum-mechanical model allows for electron states with zero angular momentum ...
... • involves 4 quantum numbers (3 more than the Bohr model) • quantum-mechanical model allows for electron states with zero angular momentum ...
Wave Particle Duality
... Erwin Schrödinger created a new, quantum model of the atom. He used much of de Broglie’s work on the wavelike properties of particles in the creation of this model. Because of Heisenberg’s Principle of Uncertainty, we cannot know both the position and the momentum of an electron at a given time. Rat ...
... Erwin Schrödinger created a new, quantum model of the atom. He used much of de Broglie’s work on the wavelike properties of particles in the creation of this model. Because of Heisenberg’s Principle of Uncertainty, we cannot know both the position and the momentum of an electron at a given time. Rat ...
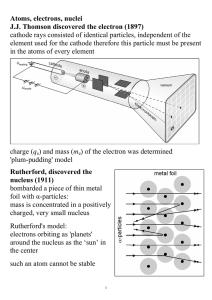
Atoms, electrons, nuclei J.J. Thomson discovered the electron (1897
... Coclusion: energy of Mercury atom cannot change continuously, but only by certain discrete values, so-called quanta Bohr's model (incorrect, but useful) electrons in an atom can only occupy certain distinct orbits around the nucleus: no radiation atoms radiate if an electron 'jumps' from one such or ...
... Coclusion: energy of Mercury atom cannot change continuously, but only by certain discrete values, so-called quanta Bohr's model (incorrect, but useful) electrons in an atom can only occupy certain distinct orbits around the nucleus: no radiation atoms radiate if an electron 'jumps' from one such or ...
study note 1 06
... What name has been given to the current theory of electronic Wave or Quantum mechanics (because it is based on a wave model of structure? matter that predicts quantized energy levels). What two kinds of waves exist? Standing and traveling. Give an example of a standing wave. Guitar string, electron. ...
... What name has been given to the current theory of electronic Wave or Quantum mechanics (because it is based on a wave model of structure? matter that predicts quantized energy levels). What two kinds of waves exist? Standing and traveling. Give an example of a standing wave. Guitar string, electron. ...
Answers
... 4) As the colour of light is slowly changed from ultraviolet to blue to red, the number of electrons will A) slowly decrease in number B) suddenly decrease in number C) become random Does this demonstrate wave or particle behaviour of light? Explain. There is a sudden decrease in the number of elect ...
... 4) As the colour of light is slowly changed from ultraviolet to blue to red, the number of electrons will A) slowly decrease in number B) suddenly decrease in number C) become random Does this demonstrate wave or particle behaviour of light? Explain. There is a sudden decrease in the number of elect ...
Particle in a box

In quantum mechanics, the particle in a box model (also known as the infinite potential well or the infinite square well) describes a particle free to move in a small space surrounded by impenetrable barriers. The model is mainly used as a hypothetical example to illustrate the differences between classical and quantum systems. In classical systems, for example a ball trapped inside a large box, the particle can move at any speed within the box and it is no more likely to be found at one position than another. However, when the well becomes very narrow (on the scale of a few nanometers), quantum effects become important. The particle may only occupy certain positive energy levels. Likewise, it can never have zero energy, meaning that the particle can never ""sit still"". Additionally, it is more likely to be found at certain positions than at others, depending on its energy level. The particle may never be detected at certain positions, known as spatial nodes.The particle in a box model provides one of the very few problems in quantum mechanics which can be solved analytically, without approximations. This means that the observable properties of the particle (such as its energy and position) are related to the mass of the particle and the width of the well by simple mathematical expressions. Due to its simplicity, the model allows insight into quantum effects without the need for complicated mathematics. It is one of the first quantum mechanics problems taught in undergraduate physics courses, and it is commonly used as an approximation for more complicated quantum systems.