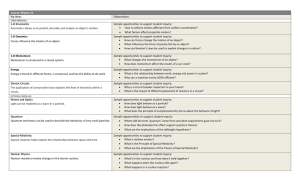
Energy - the ability to cause change. Divided into 2 categories: 1
... 2) kinetic energy - energy that is transferred and/or transformed work transfer of mechanical energy heat transfer of energy from colliding molecules (the faster they collide the higher the heat) = energy transformations occur when energy changes from one form to another chemical energy your b ...
... 2) kinetic energy - energy that is transferred and/or transformed work transfer of mechanical energy heat transfer of energy from colliding molecules (the faster they collide the higher the heat) = energy transformations occur when energy changes from one form to another chemical energy your b ...
Using the Lagrangian to obtain Equations of Motion
... so let’s try a more complicated example. We hang the pendulum from a cart of mass M and position x, acted upon by a force u in the direction of x, and moving on frictionless ...
... so let’s try a more complicated example. We hang the pendulum from a cart of mass M and position x, acted upon by a force u in the direction of x, and moving on frictionless ...
Chapter 4, 5 & 6 Work, Energy and Power Lecture Notes
... Electromagnetic energy ( see light coming from the fire on the match) 2. Conservation of energy a. Law of the Conservation of Energy states that energy cannot be created or destroyed. It simply changes from one form into another b. Part of Einstein’s theory of Relativity tells us that a small amount ...
... Electromagnetic energy ( see light coming from the fire on the match) 2. Conservation of energy a. Law of the Conservation of Energy states that energy cannot be created or destroyed. It simply changes from one form into another b. Part of Einstein’s theory of Relativity tells us that a small amount ...
Energy
... The pole is used as a means to transfer energy from the athlete, to the pole and finally back to the athlete The composition of the pole gives definite advantage to the athlete ...
... The pole is used as a means to transfer energy from the athlete, to the pole and finally back to the athlete The composition of the pole gives definite advantage to the athlete ...
Final 1
... 17. A 10 kg sphere is glued to a massless stick that is tangent to it and then spun about the axis formed by the stick. What is the sphere's rotational inertia I about this axis, if its radius is 0.2 m ? The rotational inertia of a sphere about its center is Icm = 2/5 MR2 . A. 0. 24 kg.m2 B. 0.56 kg ...
... 17. A 10 kg sphere is glued to a massless stick that is tangent to it and then spun about the axis formed by the stick. What is the sphere's rotational inertia I about this axis, if its radius is 0.2 m ? The rotational inertia of a sphere about its center is Icm = 2/5 MR2 . A. 0. 24 kg.m2 B. 0.56 kg ...
Chapter 5 Work and Energy continued
... Version 1 A force is conservative when the work it does on a moving object is independent of the path between the object’s initial and final positions. Version 2 A force is conservative when it does no net work on an object moving around a closed path, starting and finishing at the same point. ...
... Version 1 A force is conservative when the work it does on a moving object is independent of the path between the object’s initial and final positions. Version 2 A force is conservative when it does no net work on an object moving around a closed path, starting and finishing at the same point. ...
File
... How high will the ball rise? (Use Conservation of Energy to solve!) (20.4 m) 2. A sled is at the top of a 40 meter high hill. The sled and its rider have a mass of 70 kg. a. What is the GPE of sled and rider? (27,440 J) b. How fast will the sled be moving at the bottom of the hill? (28 m/s) c. If th ...
... How high will the ball rise? (Use Conservation of Energy to solve!) (20.4 m) 2. A sled is at the top of a 40 meter high hill. The sled and its rider have a mass of 70 kg. a. What is the GPE of sled and rider? (27,440 J) b. How fast will the sled be moving at the bottom of the hill? (28 m/s) c. If th ...
Physic 231 Lecture 11
... From work - energy theorem : mg ( y0 − y f ) = KE f − KE0 – From this we can see that being higher initially means that you can have a higher final kinetic energy. Thus, mg(y0-y) is the part of the stored “potential” energy, which was changed into kinetic energy as the object moves from its initial ...
... From work - energy theorem : mg ( y0 − y f ) = KE f − KE0 – From this we can see that being higher initially means that you can have a higher final kinetic energy. Thus, mg(y0-y) is the part of the stored “potential” energy, which was changed into kinetic energy as the object moves from its initial ...
1 Physics 20 10 Summer 2016 Richard In "chretsen Exam 2
... respect to the road, and the cyclist is keeping up with traffic at+25mpji_with respect to the road. (This guy's probably a pro cyclist) What is the cyclist's velocity with respect to i train? ...
... respect to the road, and the cyclist is keeping up with traffic at+25mpji_with respect to the road. (This guy's probably a pro cyclist) What is the cyclist's velocity with respect to i train? ...