Chapter 8 Rotational Dynamics continued
... DEFINITION OF ROTATIONAL KINETIC ENERGY The rotational kinetic energy of a rigid rotating object is ...
... DEFINITION OF ROTATIONAL KINETIC ENERGY The rotational kinetic energy of a rigid rotating object is ...
RG Chapter 8 KEY
... Three times as much work will be done if a barbell is lifted three times as high. This is because work is directly proportional to distance traveled. 4. At the end of the chapter, on p. 120, there are questions related to this section. Answer question 21: ...
... Three times as much work will be done if a barbell is lifted three times as high. This is because work is directly proportional to distance traveled. 4. At the end of the chapter, on p. 120, there are questions related to this section. Answer question 21: ...
Chapter 10 Momentum, System of Particles, and Conservation
... 10.2 Momentum (Quantity of Motion) and Impulse ................................................. 1 10.2.1 Average Force, Momentum, and Impulse ................................................... 2 10.2.2 Non-Constant Force and Impulse.......................................................... ...
... 10.2 Momentum (Quantity of Motion) and Impulse ................................................. 1 10.2.1 Average Force, Momentum, and Impulse ................................................... 2 10.2.2 Non-Constant Force and Impulse.......................................................... ...
Roller Coaster - Pennsylvania State University
... At the same height, a roller coaster has the same velocity wherever its position is. However, it is not that simple thing to think about its velocity at certain points only based on the knowledge of potential and kinetic energy. The reason is that there are also friction, brake, and acceleration to ...
... At the same height, a roller coaster has the same velocity wherever its position is. However, it is not that simple thing to think about its velocity at certain points only based on the knowledge of potential and kinetic energy. The reason is that there are also friction, brake, and acceleration to ...
Chapter Test A
... a. Holding a heavy box requires a lot of work. b. A scientist works on an experiment in the laboratory. c. Sam and Rachel pushed hard, but they could do no work on the car. d. John learned that shoveling snow is hard work. _____ 2. In which of the following sentences is work used in the everyday sen ...
... a. Holding a heavy box requires a lot of work. b. A scientist works on an experiment in the laboratory. c. Sam and Rachel pushed hard, but they could do no work on the car. d. John learned that shoveling snow is hard work. _____ 2. In which of the following sentences is work used in the everyday sen ...
The ball rolls up the ramp, then back down. Let +x direction be up
... C. The tractor and skateboard both go forwards; the tractor goes faster than the skateboard. D. The tractor goes forward relative to the ground; The skateboard goes backwards at the same speed. E. The tractor goes forward relative to the ground; the skateboard goes backwards at a slower speed. ...
... C. The tractor and skateboard both go forwards; the tractor goes faster than the skateboard. D. The tractor goes forward relative to the ground; The skateboard goes backwards at the same speed. E. The tractor goes forward relative to the ground; the skateboard goes backwards at a slower speed. ...
Lesson 2 Handouts and Instructional Notes
... The potential energy for every row can be found using the equation PE = m*g*h where m=510 kg and g = 9.8 m/s/s. In the first row, the total mechanical energy (KE + PE) equals 160 000 J (rounded). Since no work is done by non-conservative forces, the total mechanical energy must be 160 000 J in all t ...
... The potential energy for every row can be found using the equation PE = m*g*h where m=510 kg and g = 9.8 m/s/s. In the first row, the total mechanical energy (KE + PE) equals 160 000 J (rounded). Since no work is done by non-conservative forces, the total mechanical energy must be 160 000 J in all t ...
Atwood`s machine
... 5. Draw a free body diagram of m1 and another free body diagram of m2. Using these diagrams, apply Newton’s second law to each mass. Assume that the tension is the same on each mass and that they have the same acceleration. From these two equations, find an expression for the acceleration of m1 in ...
... 5. Draw a free body diagram of m1 and another free body diagram of m2. Using these diagrams, apply Newton’s second law to each mass. Assume that the tension is the same on each mass and that they have the same acceleration. From these two equations, find an expression for the acceleration of m1 in ...
Newton`s Second Law of Motion Chapter 5 Force and Acceleration
... proportional to the magnitude of the net force, is in the same direction as the net force, and is inversely proportional to the mass of the body.” ...
... proportional to the magnitude of the net force, is in the same direction as the net force, and is inversely proportional to the mass of the body.” ...
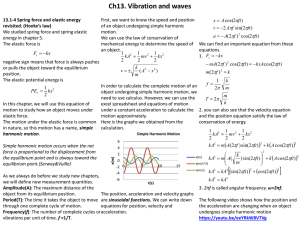
13.1-4 Spring force and elastic energy revisited. (Hooke’s law)
... object from its equilibrium position. The position, acceleration and velocity graphs Period(T): The time it takes the object to move are sinusoidal functions. We can write down through one complete cycle of motion. equations for position, velocity and Frequency(f): The number of complete cycles or a ...
... object from its equilibrium position. The position, acceleration and velocity graphs Period(T): The time it takes the object to move are sinusoidal functions. We can write down through one complete cycle of motion. equations for position, velocity and Frequency(f): The number of complete cycles or a ...
Underline your strong TEKS and circle your weak TEKS
... In the graph to the right, how many minutes did it take for the object to move 3.5 kilometers? ________________ Which of the following situations could be represented by this graph? A. A boy walks 1.5 km to the park in 10 minutes. Then he walks backwards to his house in 10 minutes. Then he runs to h ...
... In the graph to the right, how many minutes did it take for the object to move 3.5 kilometers? ________________ Which of the following situations could be represented by this graph? A. A boy walks 1.5 km to the park in 10 minutes. Then he walks backwards to his house in 10 minutes. Then he runs to h ...
Badger Chapter 28 - Forces and Motion
... Objects with no resultant force acting on them are in equilibrium. They continue in their state of motion, whether at rest or at a constant speed in a straight line. To change the motion of an object, there must be an overall force acting: a resultant or net force. It is the forces acting on an obje ...
... Objects with no resultant force acting on them are in equilibrium. They continue in their state of motion, whether at rest or at a constant speed in a straight line. To change the motion of an object, there must be an overall force acting: a resultant or net force. It is the forces acting on an obje ...