Particle in a box (PPT - 6.9MB)
... In his Scientific Autobiography and Other Papers, he stated Planck's Principle, which holds that "A new scientific truth does not triumph by convincing its opponents and making them see the light, but rather because its opponents eventually die and a new generation grows up that is familiar ...
... In his Scientific Autobiography and Other Papers, he stated Planck's Principle, which holds that "A new scientific truth does not triumph by convincing its opponents and making them see the light, but rather because its opponents eventually die and a new generation grows up that is familiar ...
Chem700 MO
... Ab-initio Theory starts from fundamental equations of quantum theory and works is up from there. Since strict analytical formula exists for energies and other system properties, many various properties can be computed, including MD potentials and interaction with light or magnetic field. However, fu ...
... Ab-initio Theory starts from fundamental equations of quantum theory and works is up from there. Since strict analytical formula exists for energies and other system properties, many various properties can be computed, including MD potentials and interaction with light or magnetic field. However, fu ...
1 - shawnschmitt
... g. Mole- the amount of particles in 12g of Carbon-12, also, the amount of substance having 6.022x1023 of any kind of particle h. half-life- the amount of time required for ½ of the mass of an isotope to decay i. metalloid- those elements that have properties of both metals and nonmetals j. Ionizatio ...
... g. Mole- the amount of particles in 12g of Carbon-12, also, the amount of substance having 6.022x1023 of any kind of particle h. half-life- the amount of time required for ½ of the mass of an isotope to decay i. metalloid- those elements that have properties of both metals and nonmetals j. Ionizatio ...
Homework 3 - barnes report
... which describes an elastic spring which can be extended but not compressed. Using symmetry properties of stationary wave functions of the harmonic oscillator, and the boundary condition at for the wave function in the potential given by Eq.(1), find the stationary wave functions and energy levels fo ...
... which describes an elastic spring which can be extended but not compressed. Using symmetry properties of stationary wave functions of the harmonic oscillator, and the boundary condition at for the wave function in the potential given by Eq.(1), find the stationary wave functions and energy levels fo ...
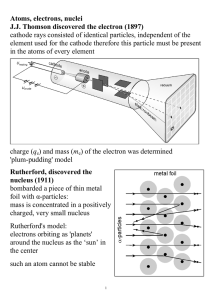
Atoms, electrons, nuclei J.J. Thomson discovered the electron (1897
... the less determined the momentum, and vice versa based on dimension analysis an uncertainty relation can be given for the case of energy · time: E t h. ...
... the less determined the momentum, and vice versa based on dimension analysis an uncertainty relation can be given for the case of energy · time: E t h. ...
CHEMISTRY – UNITS 3 and 4 REVIEW PACKET Name Date
... Fission: Takes ____ ________________ nucleus and splits into ________ _______________ nuclei. Fusion: Takes ____ ________________ nuclei and joins to form _______ ______________ nucleus. Circle the correct answer: A fission or fusion reaction is started by bombarding (hitting) a nucleus or nuclei wi ...
... Fission: Takes ____ ________________ nucleus and splits into ________ _______________ nuclei. Fusion: Takes ____ ________________ nuclei and joins to form _______ ______________ nucleus. Circle the correct answer: A fission or fusion reaction is started by bombarding (hitting) a nucleus or nuclei wi ...
Standard EPS Shell Presentation
... Danish physicist Neils Bohr proposed the concept of energy levels to explain the spectrum of hydrogen. When an electron moves from a higher energy level to a lower one, the atom gives up the energy difference between the two levels. The energy comes out as different colors of light. ...
... Danish physicist Neils Bohr proposed the concept of energy levels to explain the spectrum of hydrogen. When an electron moves from a higher energy level to a lower one, the atom gives up the energy difference between the two levels. The energy comes out as different colors of light. ...
Relativity Problem Set 9
... (c) Compute the expectation value of the kinetic energy operator K̂ in the first excited state. ...
... (c) Compute the expectation value of the kinetic energy operator K̂ in the first excited state. ...
슬라이드 1
... Hamiltonian operator energy & wavefunction (solving a partial differential equation) with ...
... Hamiltonian operator energy & wavefunction (solving a partial differential equation) with ...
Lecture 9
... measurement. We first take |ψ(x,t)|2 , and then do the experimental preparation, wait for a time t, measure the position, and repeat many times. After many repetitions, we build up a histogram for x, and compare it to |ψ(x,t)|2 . There are similar prescriptions for other quantities besides the histo ...
... measurement. We first take |ψ(x,t)|2 , and then do the experimental preparation, wait for a time t, measure the position, and repeat many times. After many repetitions, we build up a histogram for x, and compare it to |ψ(x,t)|2 . There are similar prescriptions for other quantities besides the histo ...
... Every molecule that moves into one of the interstitial sites contributes to the energy, so that for n molecules that moved the energy is n . a. What is the multiplicity function of the energy (calculate the number of possibilities that n molecules have to change their locations) b. Calculate the ...
Semiclassical calculation of electron spectra in atoms through two
... The features of the one-electron spectra in the spherically symmetric self-consistent attraction potentials have been under study in the paper [1] (also, reviews [2, 3]). Specifically, the potentials with the Coulomb singularity have been there considered. As is well known, the screening of the Coul ...
... The features of the one-electron spectra in the spherically symmetric self-consistent attraction potentials have been under study in the paper [1] (also, reviews [2, 3]). Specifically, the potentials with the Coulomb singularity have been there considered. As is well known, the screening of the Coul ...
Final
... (4) Consider the Bogoliubov de Gennes equations for an interface between a normal metal and a superconductor with gap ∆. Solve these equations for the effectively 1-dim case where an electron is incident on the interface from the normal side with sufficiently high energy to induce injection of a Bog ...
... (4) Consider the Bogoliubov de Gennes equations for an interface between a normal metal and a superconductor with gap ∆. Solve these equations for the effectively 1-dim case where an electron is incident on the interface from the normal side with sufficiently high energy to induce injection of a Bog ...