Physics 106a/196a – Problem Set 2 – Due Oct 14, 2005
... 4. (106/196) Ballistic pendulum: A wooden block of mass M hangs by a massless, rigid rod of length l from a support point. A bullet of mass m shot at the block with speed v becomes embedded in the block, causing the block and rod to swing like a pendulum. Why is this an inelastic collision? Is energ ...
... 4. (106/196) Ballistic pendulum: A wooden block of mass M hangs by a massless, rigid rod of length l from a support point. A bullet of mass m shot at the block with speed v becomes embedded in the block, causing the block and rod to swing like a pendulum. Why is this an inelastic collision? Is energ ...
3.4 Heisenberg`s uncertainty principle
... has important physical consequences. We know that the commutator of the position and momentum operator not being equal to zero means that • The respective eigenbasis are not the same • That these physical quantities of a particle cannot be simulatenously measured • measuring one, interferes with mea ...
... has important physical consequences. We know that the commutator of the position and momentum operator not being equal to zero means that • The respective eigenbasis are not the same • That these physical quantities of a particle cannot be simulatenously measured • measuring one, interferes with mea ...
Name
... 40. Differentiate between fission and fusion reactions. Fission splits a large nucleus into smaller nuclei. Fusion combines two small nuclei into one larger one. 41. Briefly describe what happens that allows you to see colors in the flame tests and the gas tubes. When energy is added to an atom, an ...
... 40. Differentiate between fission and fusion reactions. Fission splits a large nucleus into smaller nuclei. Fusion combines two small nuclei into one larger one. 41. Briefly describe what happens that allows you to see colors in the flame tests and the gas tubes. When energy is added to an atom, an ...
H-atom, spin
... What are possible values of ? For each , what are possible values of m? for each n & , how many different states are there? “subshell” for each n, how many different states are there? “shell” ...
... What are possible values of ? For each , what are possible values of m? for each n & , how many different states are there? “subshell” for each n, how many different states are there? “shell” ...
... 15 p, m. These whiskers are then thinned by ion milling to a thickness of 0.2 p, m over a length of a few millimeters. Note that the ground state for sodium is a spin 1 system is 1). For the (the total internal angular momentum experimental situation described here, the atomic Zeeman shift is smalle ...
Lectures 12-13
... and thus depend only on the quantum number n, called the principle quantum number, which takes on any value from 1 to . As usual the negative sign indicates that the electron is bound to the nucleus, i.e., the negative energy En is the energy it would take to remove an electron in state n completel ...
... and thus depend only on the quantum number n, called the principle quantum number, which takes on any value from 1 to . As usual the negative sign indicates that the electron is bound to the nucleus, i.e., the negative energy En is the energy it would take to remove an electron in state n completel ...
Nuclear Chemistry Review
... • For alpha decay, the mass number decreases by 4 and the atomic number decreases by 2. • For beta minus decay, the mass number doesn’t change and the atomic number increases by one. • For positron decay (beta plus) the mass number is unchanged and the atomic number ...
... • For alpha decay, the mass number decreases by 4 and the atomic number decreases by 2. • For beta minus decay, the mass number doesn’t change and the atomic number increases by one. • For positron decay (beta plus) the mass number is unchanged and the atomic number ...
Operators and meaning of wave function
... The problem that we have in quantum theory is, what state vector is, or what is a wave function, respectively the measurement process is also analyzed. Interpretation of quantum theory, it is basically an answer to the question what is the state vector, resp. what is a wave function. What is their p ...
... The problem that we have in quantum theory is, what state vector is, or what is a wave function, respectively the measurement process is also analyzed. Interpretation of quantum theory, it is basically an answer to the question what is the state vector, resp. what is a wave function. What is their p ...
Planck-Einstein relation, Time Dep. Schrodinger Eq., Po
... frequency and h̄ = h/2π, with h the fundamental Planck constant. So lets choose our operator ∆ to correspond to energy divided by h̄. Now we know that in classical mechanics that the energy is given by the Hamiltonian operator H = KE + PE and that this operator generates the time evolution. So in a ...
... frequency and h̄ = h/2π, with h the fundamental Planck constant. So lets choose our operator ∆ to correspond to energy divided by h̄. Now we know that in classical mechanics that the energy is given by the Hamiltonian operator H = KE + PE and that this operator generates the time evolution. So in a ...
Lie Algebras and the Schr¨odinger equation: (quasi-exact-solvability, symmetric coordinates) Alexander Turbiner
... The invariants t are defined ambiguously, they depend on chosen orbit, but always lead to rational OPH h in a form of algebraic operator with polynomial coeffs. Trigonometric case – trigonometric Weyl-invariant variables: ...
... The invariants t are defined ambiguously, they depend on chosen orbit, but always lead to rational OPH h in a form of algebraic operator with polynomial coeffs. Trigonometric case – trigonometric Weyl-invariant variables: ...
Worksheet - 1 - International Indian School, Riyadh
... 7. How many unpaired electrons are present in N? Name the principle which explains the presence of these unpaired electrons. 2 or more marks Question: 8. Write a short note on Plank’s Quantum theory. 9. Calculate the wavelength of an electron that has been accelerated in a particle accelerator throu ...
... 7. How many unpaired electrons are present in N? Name the principle which explains the presence of these unpaired electrons. 2 or more marks Question: 8. Write a short note on Plank’s Quantum theory. 9. Calculate the wavelength of an electron that has been accelerated in a particle accelerator throu ...
國立嘉義大學95學年度
... 48. Why is this reaction considered to be exothermic? (A) Because energy difference B is greater than energy difference C (B) Because energy difference B is greater than energy difference A (C) Because energy difference A is greater than energy difference C (D) Because energy difference B is greater ...
... 48. Why is this reaction considered to be exothermic? (A) Because energy difference B is greater than energy difference C (B) Because energy difference B is greater than energy difference A (C) Because energy difference A is greater than energy difference C (D) Because energy difference B is greater ...
Transparancies for Atomic Structure Section
... They are a series with specific solutions for n and l values a0 is a length ...
... They are a series with specific solutions for n and l values a0 is a length ...
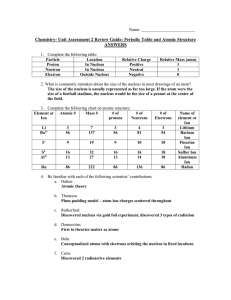
Chem Unit 2 Review Guide ANSWERS
... 17.) How are chemical reactions different than nuclear reactions? How does the Law of Conservation of Mass apply to each type of reaction? Chemical reactions only involve the atoms’ valence electrons. In a nuclear reaction, the nucleus is actually altered. The Law of Conservation of Mass holds true ...
... 17.) How are chemical reactions different than nuclear reactions? How does the Law of Conservation of Mass apply to each type of reaction? Chemical reactions only involve the atoms’ valence electrons. In a nuclear reaction, the nucleus is actually altered. The Law of Conservation of Mass holds true ...
slides introducing IR/Raman of proteins
... • As a result we have characteristic IR and Raman frequencies, ni, which are reflect bond types in the molecule. The frequency pattern forms a “fingerprint” for the molecule and its structure. • Variations due to conformation and environment give structural insight and are the prime tools for Protei ...
... • As a result we have characteristic IR and Raman frequencies, ni, which are reflect bond types in the molecule. The frequency pattern forms a “fingerprint” for the molecule and its structure. • Variations due to conformation and environment give structural insight and are the prime tools for Protei ...
What do we call a substance with more than one kind of atom
... passed straight through; some were reflected straight back to the source. The discovery led Rutherford to make several important conclusions. Using the experimental set-up shown above, what conclusions about atoms were made by Rutherford? a. each atom contains electrons b. each atom contains protons ...
... passed straight through; some were reflected straight back to the source. The discovery led Rutherford to make several important conclusions. Using the experimental set-up shown above, what conclusions about atoms were made by Rutherford? a. each atom contains electrons b. each atom contains protons ...