UNIT 6A - Gordon State College
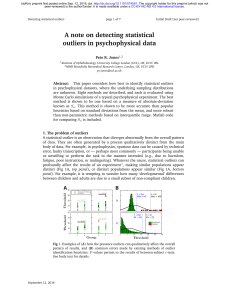
... respectively. There is no mode. 19. The mean and median are 0.81237 and 0.8161, respectively. The outlier is 0.7901, because it varies from the others by a couple hundredths of a pound, while the rest vary from each other only by a few thousandths of a pound. Without the outlier, the mean is 0.81608 ...
... respectively. There is no mode. 19. The mean and median are 0.81237 and 0.8161, respectively. The outlier is 0.7901, because it varies from the others by a couple hundredths of a pound, while the rest vary from each other only by a few thousandths of a pound. Without the outlier, the mean is 0.81608 ...
PPT Chapter 21 - McGraw Hill Higher Education
... • The most common test statistic used in this situation is a two-sample t-test (also known as a pooled t-test) • The steps for using a two-sample t-test are as follows: 1. Construct the null and alternative (two-tailed) hypotheses. H0 always states that there is no difference between the two samples ...
... • The most common test statistic used in this situation is a two-sample t-test (also known as a pooled t-test) • The steps for using a two-sample t-test are as follows: 1. Construct the null and alternative (two-tailed) hypotheses. H0 always states that there is no difference between the two samples ...
Is the average body temperature of healthy adults
... • If the sample size is relatively large (>30) both z and t tests can be used for testing hypothesis. The number 30 is just a reference for general situations and for practicing problems. In fact, if the sample is from a very skewed distribution, we need to increase the sample size or use nonparamet ...
... • If the sample size is relatively large (>30) both z and t tests can be used for testing hypothesis. The number 30 is just a reference for general situations and for practicing problems. In fact, if the sample is from a very skewed distribution, we need to increase the sample size or use nonparamet ...
Feldman-Cousins
... background with known mean b. The curves for the cases n0 from 0 through 10 are plotted. Dotted portions on the upper left indicate regions where m1 is non-zero ~and shown in the following figure!. Dashed portions in the lower right indicate regions where the probability of obtaining the number of e ...
... background with known mean b. The curves for the cases n0 from 0 through 10 are plotted. Dotted portions on the upper left indicate regions where m1 is non-zero ~and shown in the following figure!. Dashed portions in the lower right indicate regions where the probability of obtaining the number of e ...
BiostatIntro2008 Biostatistics for Genetics and Genomics Birmingham AL July 2008
... We start with the concepts of random variables and parameters. Random variables are of two types, discrete and continuous. A discrete random variable usually comes from counting and thus, usually, takes one or other of the values 0, 1, 2, . . . . The example above illustrates this: before the experi ...
... We start with the concepts of random variables and parameters. Random variables are of two types, discrete and continuous. A discrete random variable usually comes from counting and thus, usually, takes one or other of the values 0, 1, 2, . . . . The example above illustrates this: before the experi ...
A Little Stats Won't Hurt You
... quantify what happened (“What is the effect of X on Y ?”). But before any of these more complex methods can be used, the first step is always to look at the data in many different ways. The idea is to effectively describe (or summarize) the data, and then look for “interesting” features. Note, howev ...
... quantify what happened (“What is the effect of X on Y ?”). But before any of these more complex methods can be used, the first step is always to look at the data in many different ways. The idea is to effectively describe (or summarize) the data, and then look for “interesting” features. Note, howev ...
Bootstrapping (statistics)

In statistics, bootstrapping can refer to any test or metric that relies on random sampling with replacement. Bootstrapping allows assigning measures of accuracy (defined in terms of bias, variance, confidence intervals, prediction error or some other such measure) to sample estimates. This technique allows estimation of the sampling distribution of almost any statistic using random sampling methods. Generally, it falls in the broader class of resampling methods.Bootstrapping is the practice of estimating properties of an estimator (such as its variance) by measuring those properties when sampling from an approximating distribution. One standard choice for an approximating distribution is the empirical distribution function of the observed data. In the case where a set of observations can be assumed to be from an independent and identically distributed population, this can be implemented by constructing a number of resamples with replacement, of the observed dataset (and of equal size to the observed dataset).It may also be used for constructing hypothesis tests. It is often used as an alternative to statistical inference based on the assumption of a parametric model when that assumption is in doubt, or where parametric inference is impossible or requires complicated formulas for the calculation of standard errors.