Bethe-Salpeter Equation with Spin
... • Where G is the two-particle Green’s function and all the fields are in the Heisenberg representation. These are the fully dressed fields with their self-interactions. The fields ‘a’ and/or ‘b’ can be spin-1/2, spin-0 or spin-1. • The original derivation (done by both Bethe & Salpeter and Schwinge ...
... • Where G is the two-particle Green’s function and all the fields are in the Heisenberg representation. These are the fully dressed fields with their self-interactions. The fields ‘a’ and/or ‘b’ can be spin-1/2, spin-0 or spin-1. • The original derivation (done by both Bethe & Salpeter and Schwinge ...
PHYSICAL SCIENCES TIME: 3 HOURS MAXIMUM MARKS: 200
... integration by trapezoid and Simpson’s rule, Solution of first order differential equation using RungeKutta method. Finite difference methods. Tensors. Introductory group theory: SU(2), O(3). II. Classical Mechanics Dynamical systems, Phase space dynamics, stability analysis. Poisson brackets and ca ...
... integration by trapezoid and Simpson’s rule, Solution of first order differential equation using RungeKutta method. Finite difference methods. Tensors. Introductory group theory: SU(2), O(3). II. Classical Mechanics Dynamical systems, Phase space dynamics, stability analysis. Poisson brackets and ca ...
Physics 324, Fall 2001 Solutions to problem set #1 Fri. 10/12/01
... where λC = 2.4 × 10−10 cm is the Compton wavelength of the electron (eq 1-26), and mc2 = 0.51 MeV. Plugging in λ = 150 Angstrom = 1.5×10−6 cm, I get E = 6.7×10−3 eV; for λ = 5.0 × 10−8 cm, E = 6.0 eV. ...
... where λC = 2.4 × 10−10 cm is the Compton wavelength of the electron (eq 1-26), and mc2 = 0.51 MeV. Plugging in λ = 150 Angstrom = 1.5×10−6 cm, I get E = 6.7×10−3 eV; for λ = 5.0 × 10−8 cm, E = 6.0 eV. ...
Particle Zoo - University of Birmingham
... freedom which allowed formulation of Pauli exclusion principle. In 1925, it was suggested that it relates to self-rotation, but heavily criticised… only useful as a picture. In 1927 Pauli formulated theory of spin as a fully quantum object (non-relativistic). In 1928 Dirac described the relativistic ...
... freedom which allowed formulation of Pauli exclusion principle. In 1925, it was suggested that it relates to self-rotation, but heavily criticised… only useful as a picture. In 1927 Pauli formulated theory of spin as a fully quantum object (non-relativistic). In 1928 Dirac described the relativistic ...
投影片 1
... We find a very surprising result…. Both light and massive particles are not like what we expect in the ordinary situation…. ...
... We find a very surprising result…. Both light and massive particles are not like what we expect in the ordinary situation…. ...
BC Example
... On the interaction referred in point A, there are more energy transferred to the electron. This curly track requires an energy about MeV’s. On the collision between K- and proton, the proton takes some energy from the K-. This proton loses its energy as it moves slowly creating a short dark path. ...
... On the interaction referred in point A, there are more energy transferred to the electron. This curly track requires an energy about MeV’s. On the collision between K- and proton, the proton takes some energy from the K-. This proton loses its energy as it moves slowly creating a short dark path. ...
Problem set 7
... Auv = (Avu )∗ . Thus the reality of expectation values in all states implies that A is hermitian in the conventional sense. The converse is much simpler. 5. Consider a particle in a (real) potential V(x). Suppose ψ(x) is a solution of the time-independent Schrödinger equation with (real) energy eig ...
... Auv = (Avu )∗ . Thus the reality of expectation values in all states implies that A is hermitian in the conventional sense. The converse is much simpler. 5. Consider a particle in a (real) potential V(x). Suppose ψ(x) is a solution of the time-independent Schrödinger equation with (real) energy eig ...
WAVE MECHANICS (Schrödinger, 1926)
... WAVE MECHANICS * The energy depends only on the principal quantum number, as in the Bohr model: En = -2.179 X 10-18J /n2 * The orbitals are named by giving the n value followed by a letter symbol for l: l= 0,1, 2, 3, 4, 5, ... s p d f g h ... * All orbitals with the same n are called a “shell”. All ...
... WAVE MECHANICS * The energy depends only on the principal quantum number, as in the Bohr model: En = -2.179 X 10-18J /n2 * The orbitals are named by giving the n value followed by a letter symbol for l: l= 0,1, 2, 3, 4, 5, ... s p d f g h ... * All orbitals with the same n are called a “shell”. All ...
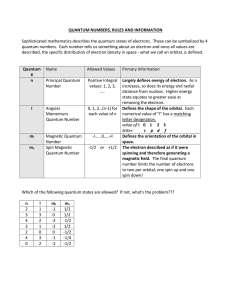
Quantum Number Table
... Largely defines energy of electron. As n increases, so does its energy and radial distance from nucleus. Higher energy state equates to greater ease at removing the electron. Defines the shape of the orbital. Each numerical value of "l" has a matching letter designation. value of l: 0 1 2 3 letter: ...
... Largely defines energy of electron. As n increases, so does its energy and radial distance from nucleus. Higher energy state equates to greater ease at removing the electron. Defines the shape of the orbital. Each numerical value of "l" has a matching letter designation. value of l: 0 1 2 3 letter: ...