Download Particle Physics and the LHC

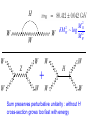
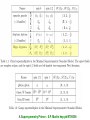
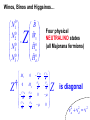
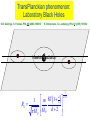
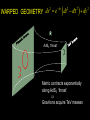
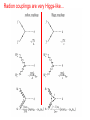
Physics Expectations at the LHC
Sreerup Raychaudhuri
Tata Institute of Fundamental Research
Mumbai, India
II
April 10,2008
IPM String School 2008, Isfahan, Iran
Plan of the Lectures
1. About the LHC
(the six-billion dollar experiment…)
2. Standard Model of Particle Physics
(what we already know…)
3. Physics beyond the Standard Model
(what we would like to know…)
4. Physics Prospects at the LHC
(what we could find in the next few years…)
Part 3
Physics beyond the Standard Model
(what we would like to know…)
Achievements of the Standard Model
• Common framework to describe weak,
electromagnetic and strong interactions
• Mechanism to have short-range interactions for
weak force
• Common mechanism for generation of mass
•Incorporates global and discrete symmetries like
quark flavor, lepton number, C, P and T, etc.
• ‘Explains’ the origin of flavour violation
• Arranges for maximal P violation in weak sector
• Accommodates CP violation in CC interactions
The Standard
Model has
(till date)
resisted all
attempts to
overturn it…
What’s wrong with the Standard Model?
We haven’t found
the Higgs boson…
We didn’t look hard
enough…
We haven’t found any
other elementary
scalars
Elementary scalars are
the simplest reps of the
Lorentz group
Why have only one scalar
doublet when there are three
fermion doublets?
Let’s find one first…
SM can accommodate more
scalar doublets easily
Can a model with 18 (20)
undetermined parameters be a
fundamental theory?
 ,  S ,sin W
MW , M H
me,  , , mu ,c ,t , md , s ,b
12 ,23 ,13 , 
2
 QCD ,  CP
That’s more of an aesthetic issue
… the SM works, doesn’t it?
There’s a desert of 17 orders of
magnitude between 102 GeV and
1019 GeV with no new physics
1.Maybe that’s the way Nature is…
2.The SM may well be a low-energy
effective theory
Folklore:
Every time we probed a new energy
scale, we discovered new substructures and new interactions…
Symmetries observed at lower energy
scales indicate different arrangement of
these substructures…
…periodic table… eightfold way…
We now have three generations of fermions with
repeated properties…
Historical development is not a
valid scientific reason…
Fermion replication may well be
(a) accidental, or
(b) a sign of some (broken) global
symmetry, e.g. SU(3), S3
The strong interactions are not
unified with the electroweak one…
All the generators of SU(3)C commute with
all the generators of SU(2)LU(1)Y
1. Unification would require a higher
gauge symmetry at higher energies
— GUTs
2. There is no compelling empirical
reason to unify strong with
electroweak interactions….
Neutrino masses are unnaturally small
11
mt ~ 10 m1
u, c, t
d , s, b
 1,2,3
eV
meV
e,  ,
eV
keV
MeV
GeV
TeV
The Naturalness Argument
• If there are very large/small parameters in
a quantum theory, there must be a
good reason why they are so small….
• In general, there will be large quantum corrections to
such parameters in higher orders of perturbation
theory, in terms of other parameters which
are not so small.
• These quantum corrections can cancel out only if there
is some underlying symmetry causing them to
cancel... The parameter is said to be ‘protected’
by the symmetry.
• This applies specially to masses and couplings, which
are known to run.
Neutrinos have always been a slight embarrassment
in the Standard Model
• Earlier they were thought to be massless 
accommodated in the Standard Model by
assuming there is no right-handed neutrino
• All that is special about a right-handed neutrino
is that it is a gauge singlet Q  T3  12 Y
• There is as much reason to suppose that
gauge singlet fermions exist as there is to
suppose that they do not exist
• Hence the huge number of models for neutrino
mass(es) constructed in the 1980s
The SuperKamiokande Experiment
SuperK has changed the scene  since
neutrinos undergo flavor oscillations they
must have nonzero masses
But the masses are very very small…. Why?
Are we really bound to answer this question?
The mass of the neutrino is not just a mass,
it is also the strength of the Yukawa interaction of
the neutrino with Higgs bosons…similarly for top
quarks…
LYukawa
 m

   L R H  m L R   H .c.
 v

Variation in interaction strength over 11 orders of
magnitude is like the difference between weak and
electromagnetic interactions  does this mean a new
type of force between neutrinos and Higgs bosons?
There is an elegant explanation…
The Seesaw mechanism:
Lmass   nL
 0 Vew  nR 
NL  
   H .c.
 Vew M   N R 
Vew
N ( x)
Diagonalise:  ( x )  n( x ) 
M
2
Vew
M ~ 100 TeV
m 
M
Majorana mass:
nR   nL 
c
; NR   NL 
c
Many variations of the simplest seesaw
mechanism exist 
many of them proposed to explain the
large mixing angle found by SuperK
many of them require the right-handed
neutrino to have some special
properties… Majorana mass….
All require a heavy mass scale M
 new physics at scales of TeV or
higher… SM is inadequate…
1. The seesaw argument is pretty but
not empirically compelling…
2. In the SM fermion masses are put
in by hand anyway…we do not
even try to understand them…
3. Hierarchy of Yukawa couplings may just be the
way Nature is…
4. Fermion masses get at best logarithmic
corrections from high scale physics because of
chiral symmetry… naturalness is not such a
serious problem…
The Higgs boson
mass is not UV stable
Umm… er….
The Higgs Boson and the
Hierarchy Problem
A light Higgs boson?
• The mass of the Higgs boson M H is an
undetermined parameter in the Standard Model
• The scalar self-coupling grows with
M    v
2
H
1
2
2
2
MH
and becomes non-perturbative around
M H  800 GeV
• Electroweak precision data predict a light Higgs with
M H  237 (480) GeV
• LEP saw a few candidates around 114 GeV
Higgs candidate: e+e- bbbb, with 3 secondary vertices (20.09.2000)
LEPEWWG 2001
M H  237 GeV
at 68% C.L.
Large uncertainties
because of the weak
dependence on Higgs
mass : log MH
M H  11469
45 GeV
M H  480 GeV
at 95% C.L.
• At the LHC we are almost sure to find
a light Higgs boson…
– What if we don’t find it?
• We will have to find an equally good
mechanism to generate masses for all
elementary particles
• We must explain the radiative
corrections to the W-boson self-energy
which are precisely measured
• We must explain how WW scattering
does not violate perturbative unitarity
H
W
W
W
M
 M ~ log
W
M
2
W
W
Z
W
W

W
W
H
2
H
2
W
W
W
Sum preserves perturbative unitarity : without H
cross-section grows too fast with energy
• If we do find it?
We must
understand why
it is so light…
This is not just a piece of theoretical fussiness….
The Standard Model is a quantum (field) theory
• Even tree-level results are just the lowest order
in perturbation theory
• One-loop predictions are also tested to great
accuracy at LEP etc.
• It is meaningless to consider only tree-level
results, unless we can prove that higher
orders give small contributions
• Higher order corrections to Higgs boson mass
are very large…
The scalar sector of the Standard Model is basically
4

a
theory coupled to a (nonAbelian) gauge
theory and some fermion multiplets
H
H
 Higgs boson has quartic self couplings
 there are self-energy corrections with

H
H
quadratic divergences
 M H2   2  soft  finite
H
 is the cutoff for the SM
H

H
This effect cannot
be wished away…
The Hierarchy Problem was pointed out by ‘Hooft
more than thirty years ago. Over these three
decades it has become clear that it cannot be
• ignored
(SM is a quantum theory)
• removed by renormalisation-type tricks
(reappears at next order)
• resolved without some new physics
(at the electroweak or TeV scale ?)
Beyond the
Standard Model
Q. How can we protect the Higgs boson mass
from these large quantum corrections?
Only two ways:
• bring down the cutoff  to the TeV scale
• composite models
• brane-worlds
 new physics at a TeV
• introduce some new symmetry into the theory
• supersymmetry  symmetry must be
broken around TeV…
• little Higgs models
Further Hints of New Physics:
• CP-Violation: baryon asymmetry
• Cold dark matter: what could it be?
• Cosmological constant:  > 0
Modelling is heavily
dependent on
individual prejudices
Do not indicate the
TeV scale per se
Grand Unification
Unification of forces has been a cherished
goal of scientists from the days of Demokritos
They say some things are sweet 
They say some things are sour 
But in reality there are only atoms and the void…
(fanciful)
model of unification…
ModernEarly
Theories
of unification:
Maxwell (gauge theoretic approach)
 Einstein (geometric approach)
 Glashow-Salam-Weinberg

Electroweak unification shows up very
nicely in experimental results
Deep inelastic scattering data from the HERA collider at
DESY, Hamburg
Programme of unification:
• Electric + magnetic = electromagnetic
• Electromagnetic + weak = electroweak
• Electroweak + strong = grand unification
• GUT + gravity = super-unification
 ( 2 )
2
Running
 (Q ) 
2
2
 ( )
Q
coupling
1
f (n) log 2
3

constants
U. Amaldi et al 1996
 GUT ~ 1016 GeV
SUSY SU(5)-based one-step grand unification
Positive thinking:
• Unification of forces is not just a theoretician’s
dream but it is the culmination towards
which all fundamental science tends
•Supersymmetric SU(5) theories did provide a
simple and elegant model for one-step grand
unification with SUSY particles at a few TeV…
predicts a rather small p
• Problems with proton lifetime can be easily
resolved by considering SUSY SO(10) GUTs…
DEVIL’S ADVOCATE
• Hierarchy problem remains anyway GUT » TeV
• Maybe unification of forces occurs in various
steps at different energies, the lowest of
which may be far beyond a TeV
• Maybe unification of couplings occurs only in a
(string) theory at the Planck scale
• Maybe gauge theories are only effective theories at low
energies and when we go higher something
completely different happens
• Maybe there is no single force in the Universe and Grand
Unification is just a dream
• In any case, speculating about 16 orders of magnitude is
useless without more information
Grand Unification is still very much
a conjecture…
Technicolour
• Inspired by superconductivity, quark model and
QCD…
• Just as mesons are composites of quarks and pion
masses are related to QCD scale in a SU(3)
gauge theory…
...so Higgs bosons are composites of technifermions and electroweak scale is related to a
technicolour scale in a SU(N) gauge theory
SU(N)
Idea is simple and elegant ─ implementation is not
• How are quark & lepton masses obtained?
Need to relate composite Higgs to fermions…
 Extended technicolour (ETC)
GETC  SU ( N )TC  SU (3)C
Symmetry-breaking scale is around 10-100 TeV
Generates quark and lepton masses through
self-energy corrections with composite Higgs;
also predicts heavy technipions around 100 GeV
– few TeV
ETC models fail to explain:
• small value of K  K
0
0
mixing
• precision data on the S parameter
• the large t quark mass
 Invention of walking technicolour
 TC (Q2) evolves very slowly
• small contribution to K  K mixing
0
0
• small contribution to S parameter
Large top quark mass is still a problem in ETC models
 Invention of topcolour
 new (gauge) interaction: leads to formation of
 tt 
condensate  Higgs-like particle
State of the art: topcolour-assisted ETC
 SU (3) U (1) tb  SU (3) U (1) ud ,cs  SU (3)C U (1)Y
TeV
Quite a bit of fine-tuning has to be done:
still predicts mt ≈ 250 GeV
 Invention of top-seesaw models
Getting
messy…
Compositeness is still a very attractive idea
• Too complicated to be credible: epicycles?
• Too slavish in following QCD? Naïve?
• TeV scale interactions may be non-gauge
interactions after all
Copernican theory ● Sommerfeld atom ● Sakata model
Supersymmetry
and the MSSM
fermions
Qa , Q
a
N 1
bosons
In a supersymmetric theory the bosons and fermions
have the same mass and couplings
H
M H2  g 2 2  soft  finite
g2
H
g
g2
H
M H2   g 2 2  soft  finite
~
H
H
H
g
g
Quadratic divergences cancel
 no hierarchy problem
If SUSY partners have the same masses as
the Standard Model particles they should have
been discovered by now…
ergo, they must be heavy
 SUSY must be badly broken
Spontaneous breaking is ruled out
• There are no goldstinos
• All the superpartners are heavy (sum rule)
Must have explicit SUSY-breaking terms
Constructing the MSSM
Use the superfield formalism…
Scalar superfield :
Vector superfield:
ˆ   ,  , F 

V̂   v  ,  , D 
Chiral spinor
Majorana spinor
Every SM particle is embedded in the appropriate
superfield…
Notation: use the symbol for the SM particle with
carat and tilde…e.g.
L. electron s.f.
eˆL  (eL , eL , FeL )
L. selectron
^
^
^
^
^
^
^
A Supersymmetry Primer : S.P. Martin hep-ph/9709356
General form of a SUSY gauge + Yukawa + 4 theory
ˆ
† gV
ˆ
L   i i e ˆ i

ˆ b 
ˆ ˆ
ˆ ˆ ˆ
  i ai 
i
ij i  j  cijk  i  j  k

 H.c.
superpotential
ˆL eˆL e
g
σa g ' ˆ
ˆ
Wa  B
2 2

a
ˆL 
 eˆ 
 L
Gauge-fermion
Interactions:
  eL  W ,
  eL  W ,
  eL  W ,
  eL  W ,
   Z ,
   Z ,
   Z ,
   Z ,
Yukawa
Scalar e.d.
eL  eL  Z ,
eL  eL  Z ,
eL  eL  Z ,
eL  eL  Z ,
eL  eL  
eL  eL  
eL  eL  
eL  eL  
Can use this prescription to construct MSSM
with unbroken SUSY
Require to add explicit SUSY-breaking terms
must be soft (i.e. positive dimension coupling
constants) to avoid new quadratic divergences
Gaugino mass terms
Higgsino mass terms
Trilinear terms
Sfermion mass terms
Origin of all these terms requires an explanation
outside of the MSSM
In a SUGRA model, SUSY can be broken spontaneously in a
‘hidden sector’, where the goldstinos are absorbed into the
gravitino by a super-Higgs mechanism… the SUSY breaking is
then communicated to the visible sector by gravity, creating soft
SUSY-breaking effective operators … note that the physical and
‘hidden’ sectors can be in the same spacetime… it’s just that they
do not interact (other than gravity, of course)…
MSSM Superpotential
^
^
^ ^
^
^ ^
^ ^
L
^
L
L
^
Colour and flavour indices are suppressed :
3 3 matrices
Doublets are combined as SU(2) products:
 '   ab a b '

^


0
ˆ
ˆ
ye ˆ H d  eˆL H d eR
Interactions:
  e  H d ,

  e  Hd ,

  e  Hd ,
 e  H  H ,

d
0
d
Yukawa
Seagull terms
eL  eL  H d0
0
eL  eL  H d
0
eL  eL  H d
0
0
eL  eL  H d  H d , etc.
Electroweak symmetry-breaking causes many of
the gauge-SUSY eigenstates to mix…
 H u0 
Higgs bosons H u    
 Hu 
H  , H 0 , h0 , A0
 H d 
Hd   0 
 Hd 
vu
tan  
vd
Physical Higgs bosons:
 G   cos 
 
 H    sin 

Charged Higgs
  
sin    H u
 
cos   H 
d

*


 G 0   cos 



0
Neutral pseudoscalar A
    sin 
sin    Im H u0 

0
cos    Im H d 
 h0   cos 
 0
Heavy neutral scalar  H    sin 
sin    Re H u0 

0
cos    Re H d 
Light neutral scalar
 mh  M Z cos 2  140
91 GeV
GeV
+ Radiative Corrections
A light Higgs boson is the most robust
phenomenological prediction of the MSSM
G. Weiglein, Nature (2004)
Winos, Binos and Higgsinos…
N
N

N

N
0
1
0
2
0
3
0
3






†
Z
 B 
W 
 3
 H u0 
 0
 Hd 
Z
 M1

 0

  g 'vd
2

 g 'vu
 2

0
M2
gvd
2

gvu
2
g 'vd
2
gvd
2
0

Four physical
NEUTRALINO states
(all Majorana fermions)


gvu 

2 
 


0 
g 'vu
2
Z
is diagonal
v v v
2
u
2
d
2
Winos, Binos and Higgsinos…
Two physical CHARGINO states (both Dirac
fermions) from mixing:
 C1   W  
    
 C2   H 
Roughly …
Two physical SQUARK states (both scalars)
from mixing of left- and right-squarks through
electroweak vev…
With CKM effects, we get 66 squark mass/mixing matrices
Sparticle Spectrum (neglecting small fermion masses)
•The MSSM has 124 unknown parameters!
• Constrain it in various ways. e.g. embed in a
SUSY-GUT
• Different mechanisms for SUSY-breaking lead to
different predictions for SUSY mass spectrum
─ Gravity mediation (mSugra)
─ Gauge mediation (GMSB)
─ Anomaly mediation (AMSB)
─ Gaugino mediation
Phenomenological consequences depend very
strongly on the mass spectrum and couplings
S.P. Martin hep-ph/9709356
S.P. Martin hep-ph/9709356
Masses
→
Sample Sparticle spectra:
mSUGRA
GMSB
Phenomenological predictions are somewhat different in
the two cases…
Supersymmetry is probably the best solution to
the hierarchy problem
Also has aesthetic appeal and close link with
Planck-scale physics
• Proliferation of fields and parameters
• SUSY-breaking schemes are ad hoc
• Phenomenology is very model-dependent
SUSY predicts a light Higgs boson which we must
find at the LHC to keep MSSM alive…
Brane worlds
• The Universe has more than 1+3 dimensions, but
the Standard Model fields (us!) are confined to
a 1+3 dimensional hyper-surface (brane)
• The extra dimensions are compactified
• Gravity is free to propagate in the extra
dimensions
• Gravity is as strong as the electroweak
interaction, but appears weak on the brane
• TeV-scale experiments probe the `strong’ gravity
sector
 there is new physics at a TeV
There is no hierarchy problem
Large extra dimensions
• There are 2 or more compact dimensions of size as
large as ~ 100 m
• The wavefunction of the ‘strongly’-interacting
graviton spreads out in all the dimensions: only
a small part intersects the brane
• Gravitons produced in a collision can fly off into the
extra dimensions, carrying energy-momentum
which would seem to disappear from the brane
(missing energy-momentum signatures)
• Virtual graviton exchanges can look like neutral
current interactions
FLAT GEOMETRY
ds  dt  dx  dy
2
2
2
2
Open
strings

Gauge
fields
Closed
strings

Massless
Gravitons
Einstein-Hilbert action in 4+d dimensions
Sˆ 
1
4
d
ˆ
ˆ
d
x
d
y

g
(
x
,
y
)
R
B
B

ˆ
16 GB
VB
4

d
x  g ( x) R + ...

16 Gˆ B
1
4

d
x  g ( x) R + ...

16 GN
Gˆ N
 GN 
Vd
 Gˆ N  GNVd
Integrate over
bulk for large
objects
Cis-Planckian regime
Gˆ N can be large if
Vd is large

GN m
r / 
Eöt-Wash experiment m (r ) 
1e
r
2003
data

For ||~1
 < 150 m
Eventually
 < 60 m
Compare with
P
~ 1029  m
Bulk scale versus Planck scale
2
GN  2 ;
MP
Gˆ N 
2
;
2 d
ˆ
MP
Gˆ N  GNVB
2
2 d
 MP 
 Mˆ P  

 V 
 B
2
M P  2 d


d
 2 RC  2d
on a d-torus
Eöt-Wash experiment
Possible to have
TeV effects if d > 2
Feynman Rules for the ADD model
(n) 
Sint    d 4 x   h( n )T( 


T ( SM ) 
SM )
2
n
all scalars
Han, Lykken and Zhang, Phys Rev D59, 105006
all gauge bosons
all fermions
On the brane…
Tower of Kaluza-Klein states :
Mn 
n2
 2 RC 
2
(n)
G
( x)
n12  n22  ...  nd2

2 RC
Spacing between states :
1
M n ~
RC
~ MP
if RC ~
P
~ 0.01 eV if RC ~ 0.001 cm
No of contributing states :
s
100 GeV
~
~ 1013
M n 0.01 eV
A massless bulk graviton is like a huge swarm of
massive graviton fields on the brane — quasicontinuum
Sum over KK states can be done using the quasi-continuum
approach
 (M
s
n
n
)   dM  ( M ) ( M )
0
 (M ) 
RCd M d  2
 4 
d /2
(d / 2)
Sum over propagators…

sM
n
2
2
n
 i

 (d , s)
Mˆ P4
1
 4
MS
reduces to a contact interaction…
Collider physics with gravitons/dilatons:
Graviton tower couples to every particle-antiparticle
pair
Blind to all quantum numbers except energymomentum
Each Kaluza-Klein mode couples equally, with
strength 
Tower of Kaluza-Klein modes builds up collectively to
an observable effect
Individual graviton modes escape detection
 missing pT
TransPlanckian phenomenon:
Laboratory Black Holes
S.B. Giddings, S. Thomas, PRL 65 (2002) 056010
S. Dimopoulos, G. Landsberg, PRL 87 (2001) 161602
Hawking radiation

d

8

1

1
m
2

RS 
 Mˆ P  Mˆ P d  2
 


1
d 1
Only semi-classical treatment possible
 BH ~  R ~ TeV
2
S
2
~ 400 pb
About 107 micro black holes per year @LHC
Rapid evaporation by Hawking radiation
1  2m 



MS  MS 
(3n 1)
( n 1)
 10
25
s
All possible particles are produced in the black hole
decay… one just looks for such events with a huge
number of uncorrelated particles shooting out in all
directions….
Warped gravity
• There need be only one extra dimension, but it is
compactified on S1/Z2
• There are two branes at the orbifold fixed points
• The Standard Model lives on one brane; `strong’
gravity on the other
• The graviton wavefunction is exponentially damped
across the extra dimension  a ratio of about
1/
12 enough to reproduce the electroweakPlanck scale hierarchy
• On our brane gravitons appear like spin-2 WIMPs
WARPED GEOMETRY ds  e
2
 ky
 dt
2
 dx
2
  dy
AdS5 ‘throat’
Metric contracts exponentially
along AdS5 ‘throat’

Gravitons acquire TeV masses
2
Modulus stabilization and the radion:
Warping is extremely sensitive to RC
e
 kRC 
~ 10
16
if kRC  11.7
Consider the radius of the extra dimension as a dynamical
object :
2
2 kT ( x ) 
2
2
ds  e
g  ( x)  T ( x) d
Modulus field : T ( x )
Radion field :
S grav
( x) 
24 Mˆ 3
k
e  k T ( x )
1
1
2 Mˆ 3 

2

  d x  g ( x) 2         k
12


4
Radion is a free field i.e. it can assume any value  same
for modulus
Need for modulus stabilization
Goldberger-Wise mechanism :
Assume a bulk scalar field
B ( x, y )
Write down a B4 theory in the bulk and on the two branes…
Solving the equation of motion for
(x) and integrating over y leads to
potential with a steep minimum at
V (ky )
v0
4k 2
kRC  k T ( x) 
log
2
 MB
v
Can assume the desired value (≈ 11.7) without
assuming any large/small numbers…
k T
Undetermined parameters: radion mass M  & radion vev   
Radion couplings are very Higgs-like…
Extra dimensions are an exciting idea
Provide an intimate link with structure of
spacetime and technical problems in particle
physics
• None of the models is completely free from
fine-tuning
• There is no way to determine the
number of the extra dimensions
• We do not understand dynamically why
some of the dimensions are compact
• Phenomenology is highly model-dependent
–only spin-2 graviton is universal
Little Higgs models
Grew out of extra dimensions and borrowed many
ideas from technicolour theories
Simplest theory is the littlest Higgs model
• Above about 10 TeV there is a global SU(5) gauge
symmetry, with a locally gauged subset
 SU (2) U (1)1   SU (2) U (1)2
10 TeV
 SU (2) L  U (1)Y
10 TeV
SU (5)  SO(5)
•
Global symmetry breaking produces 14 Goldstone bosons
10 ,30 ,21/ 2 ,31
Higgs mass is protected
The Higgs is actually a pseudo-Goldstone boson
• There are massive gauge bosons W’ and B’ at the
TeV scale ─ radiative corrections generate
(negative) Higgs mass terms (ColemanWeinberg mechanism)
• Quadratic divergences in the Higgs mass
generated by W and B cancel with those
generated by W’ and B’ (negative signs are
generated by group-theoretic factors)
•
Top quark generates a large Higgs mass
correction; this is cancelled by a heavy pair of
vectorlike fermions
Hierarchy problem disappears: lots of TeV physics
Little Higgs models are ingenious
Provide a non-supersymmetric way to cancel
quadratic divergences
• Too clever by half
• The gauge symmetry is completely ad hoc
• New fields, interactions and symmetries
have been thrown in as and when
required…
• Experience shows that Nature is generally
simple
String Theory
Strings naturally live in more than 1+3
dimensions (26, 10, …)
If some of these dimensions are large,
in the ADD sense, we could have strong
gravity at a few TeV, (maybe) grand
unification at a few TeV, and stringy
effects at a few TeV
Could the LHC then see stringy effects?
ECM
MP
Landscape of string theoretic vacua
Proposed as a solution to the cosmological constant problem
Limited number of these vacua can lead to structure formation
Choice of compactification scheme is limited,
e.g. KKLT: modulus mediation, mirage mediation
Construct a low-energy spectrum and ensure
that it is consistent with
Compare different signatures at the LHC…
Kane, Kumar, Shao 2007
Y.G.Kim 2007
Y.G.Kim 2007
Landscape ideas (anthropic principle)
are still controversial
New ideas, model variants, etc. are coming thick
and fast…
Most of them essentially propose a new sparticle
spectrum
A particular sparticle spectrum does not
necessarily imply a particular compactification
scheme
More phenomenological study is required…
How to search for New
Physics at the LHC…