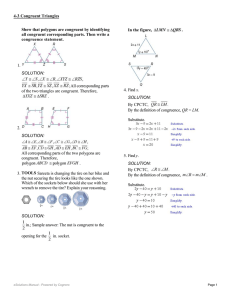
Show that polygons are congruent by identifying all
... ; The corresponding parts of the triangles are congruent, therefore the triangles are congruent. b. ; We are given that , and corresponds with Since corresponding parts of congruent triangles are congruent, c. we are given that and corresponds with Since corresponding parts of congruent tr ...
... ; The corresponding parts of the triangles are congruent, therefore the triangles are congruent. b. ; We are given that , and corresponds with Since corresponding parts of congruent triangles are congruent, c. we are given that and corresponds with Since corresponding parts of congruent tr ...
quantum computing
... mainly as machine processes in the 20th century, and it will be thought of mainly as Nature processes in the 21st century. We cannot tell, of course, how much of this vision will be true. Currently, we see vigorous, interesting and, we expect, very important attempts to go much deeper than before in ...
... mainly as machine processes in the 20th century, and it will be thought of mainly as Nature processes in the 21st century. We cannot tell, of course, how much of this vision will be true. Currently, we see vigorous, interesting and, we expect, very important attempts to go much deeper than before in ...
Ultracold Fermions in Two-Dimensional Planes with Dipolar
... in the rovibrational ground state. The strategy which lead to success was to first cool down atoms and then coherently convert them to ground state molecules at low temperatures without heating the sample. Mainly this is done by the use of Feshbach resonance to switch the interaction after the cooli ...
... in the rovibrational ground state. The strategy which lead to success was to first cool down atoms and then coherently convert them to ground state molecules at low temperatures without heating the sample. Mainly this is done by the use of Feshbach resonance to switch the interaction after the cooli ...
9. QUANTUM CHROMODYNAMICS 9. Quantum chromodynamics 1
... again parametrized in terms of a constant Λ. Note that Eq. (9.5) is one of several possible approximate 4-loop solutions for αs (µ2R ), and that a value for Λ only defines αs (µ2R ) once one knows which particular approximation is being used. An alternative to the use of formulas such as Eq. (9.5) i ...
... again parametrized in terms of a constant Λ. Note that Eq. (9.5) is one of several possible approximate 4-loop solutions for αs (µ2R ), and that a value for Λ only defines αs (µ2R ) once one knows which particular approximation is being used. An alternative to the use of formulas such as Eq. (9.5) i ...
Show that polygons are congruent by identifying all congruent
... are congruent? Explain your reasoning. SOLUTION: To prove that all of the hoops are congruent, use the diameter, radius, or circumference. Sample answer: Two circles are the same size if they have the same diameter, radius, or circumference, so she can determine if the hoops are congruent if she m ...
... are congruent? Explain your reasoning. SOLUTION: To prove that all of the hoops are congruent, use the diameter, radius, or circumference. Sample answer: Two circles are the same size if they have the same diameter, radius, or circumference, so she can determine if the hoops are congruent if she m ...
Quantum Wavepacket Dynamics in Molecular and Trapped Ion Systems Dong Wang
... pattern is very stable in time [25]. All examples we mentioned above belong to this type. The partial wavepackets are propagating in the same direction and have the same momentum. The other type of interference is observed between counterpropagaing partial wavepackets. The interference takes place o ...
... pattern is very stable in time [25]. All examples we mentioned above belong to this type. The partial wavepackets are propagating in the same direction and have the same momentum. The other type of interference is observed between counterpropagaing partial wavepackets. The interference takes place o ...
What is Hyperbolic Geometry? - School of Mathematics, TIFR
... Department of Mathematics, RKM Vivekananda University. ...
... Department of Mathematics, RKM Vivekananda University. ...
Entanglement Theory and the Quantum
... Quantum mechanics led us to reconsider the scope of physics and its building principles, such as the notions of realism and locality. More recently, quantum theory has changed in an equally dramatic manner our understanding of information processing and computation. On one hand, the fundamental prop ...
... Quantum mechanics led us to reconsider the scope of physics and its building principles, such as the notions of realism and locality. More recently, quantum theory has changed in an equally dramatic manner our understanding of information processing and computation. On one hand, the fundamental prop ...
1.1 - ChaosBook.org
... This book is a result of collaborative labors of many people over a span of several decades. Coauthors of a chapter or a section are indicated in the byline to the chapter/section title. If you are referring to a specific coauthored section rather than the entire book, cite it as (for example): C. Ch ...
... This book is a result of collaborative labors of many people over a span of several decades. Coauthors of a chapter or a section are indicated in the byline to the chapter/section title. If you are referring to a specific coauthored section rather than the entire book, cite it as (for example): C. Ch ...
Strong coupling QCD
... theoretical physics.” “EMPTY space may really be empty. Though quantum theory suggests that a ...
... theoretical physics.” “EMPTY space may really be empty. Though quantum theory suggests that a ...
Classification of topological quantum matter with
... our understanding of topological states of quantum matter. While many properties of condensed matter systems have an analogue in classical systems and may be understood without referring to quantum mechanics, topological states and topological phenomena are rooted in quantum mechanics in an essentia ...
... our understanding of topological states of quantum matter. While many properties of condensed matter systems have an analogue in classical systems and may be understood without referring to quantum mechanics, topological states and topological phenomena are rooted in quantum mechanics in an essentia ...
Topological phases and polaron physics in ultra cold quantum gases
... Since the advent of quantum mechanics, physicists believe to have at hand a microscopic description of almost any phenomenon than can be observed at moderate energy scales. This typically means that we can write down a Hamiltonian Ĥ (or a Lagrangian) which describes the relevant microscopic degrees ...
... Since the advent of quantum mechanics, physicists believe to have at hand a microscopic description of almost any phenomenon than can be observed at moderate energy scales. This typically means that we can write down a Hamiltonian Ĥ (or a Lagrangian) which describes the relevant microscopic degrees ...
quant-ph/0608013 PDF
... • J. I. Latorre and R. Orús. Adiabatic quantum computation and quantum phase transitions. Phys. Rev. A, 69:062302, 2004. • R. Orús, J. I. Latorre, and M. A. Martı́n-Delgado. Systematic analysis of majorization in quantum algorithms. Eur. Phys. J. D, 29:119, 2004. • R. Orús, J. I. Latorre, and M. ...
... • J. I. Latorre and R. Orús. Adiabatic quantum computation and quantum phase transitions. Phys. Rev. A, 69:062302, 2004. • R. Orús, J. I. Latorre, and M. A. Martı́n-Delgado. Systematic analysis of majorization in quantum algorithms. Eur. Phys. J. D, 29:119, 2004. • R. Orús, J. I. Latorre, and M. ...
reactive molecular collisions
... the only method currently available that is general enough to treat the wide range of problems facing the dynamicist. Trajectory calculations of atom-diatom reactions now appear routinely; the treatment today is basically that originally described by Karplus et al (28) in 1965. In the last year alon ...
... the only method currently available that is general enough to treat the wide range of problems facing the dynamicist. Trajectory calculations of atom-diatom reactions now appear routinely; the treatment today is basically that originally described by Karplus et al (28) in 1965. In the last year alon ...