* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download CS 256: Neural Computation Lecture Notes
Cognitive neuroscience wikipedia , lookup
Signal transduction wikipedia , lookup
Convolutional neural network wikipedia , lookup
Caridoid escape reaction wikipedia , lookup
Node of Ranvier wikipedia , lookup
Apical dendrite wikipedia , lookup
Artificial general intelligence wikipedia , lookup
Central pattern generator wikipedia , lookup
Membrane potential wikipedia , lookup
Subventricular zone wikipedia , lookup
Recurrent neural network wikipedia , lookup
Mirror neuron wikipedia , lookup
Axon guidance wikipedia , lookup
Neural oscillation wikipedia , lookup
Holonomic brain theory wikipedia , lookup
Neural engineering wikipedia , lookup
Premovement neuronal activity wikipedia , lookup
Resting potential wikipedia , lookup
Multielectrode array wikipedia , lookup
Action potential wikipedia , lookup
Neural coding wikipedia , lookup
End-plate potential wikipedia , lookup
Types of artificial neural networks wikipedia , lookup
Clinical neurochemistry wikipedia , lookup
Nonsynaptic plasticity wikipedia , lookup
Circumventricular organs wikipedia , lookup
Metastability in the brain wikipedia , lookup
Pre-Bötzinger complex wikipedia , lookup
Synaptogenesis wikipedia , lookup
Neurotransmitter wikipedia , lookup
Optogenetics wikipedia , lookup
Electrophysiology wikipedia , lookup
Neuroanatomy wikipedia , lookup
Feature detection (nervous system) wikipedia , lookup
Biological neuron model wikipedia , lookup
Development of the nervous system wikipedia , lookup
Molecular neuroscience wikipedia , lookup
Single-unit recording wikipedia , lookup
Chemical synapse wikipedia , lookup
Synaptic gating wikipedia , lookup
Stimulus (physiology) wikipedia , lookup
Neuropsychopharmacology wikipedia , lookup
CS 256: Neural Computation Lecture Notes
Chapter 1: Introduction
• Problems in vision
• The Computer and the Brain
• Biological neurons
• Action potentials
• McCulloch-Pitts neurons
• Linear (and polynomial) threshold units
• Feedforward neural networks
• Feedback neural networks
AT X at 11:30 AM on January 18, 2011.
Compiled by L
E
Neurons Compute!
Thinking is brought about by neurons and we should not use
phrases like “unit activity reflects, reveals, or monitors thought
processes,” because the activities of neurons, quite simply, are
thought processes.
Horace B. Barlow, “Single units and sensation: a neuron doctrine for perceptual psychology?”
Perception, 1, 1972, pp. 371–394. (Reprinted in J. A. Anderson and E. Rosenfeld, ed.,
Neurocomputing, vol. 2, MIT Press, Cambridge, MA, 1990, pp. 218–234, available on course
reserve in Bailey-Howe Library.)
Vision: Stereopsis
David Marr, Vision, W. H. Freeman, San Francisco, 1982, p. 9.
Vision: Grouping
David Marr, Vision, W. H. Freeman, San Francisco, p. 101.
The Computer vs. The Brain
Quantity
Electronic Computer (CMOS)
Human Brain
Mass
1 kg
1 kg
Volume
< 10−6 m3
10−3 m3
# Units
1010 gates
1010 neurons,
1014 synapses
Gate Density
1016 gates/m3
1017 synapes/m3
Gate Dimensions
10−6 m
10−5 to 10−9 m
Period
10−9 sec
10−2 sec.
Signal Amplitude
2V
50 mV
Pulse Duration
10−9 s
10−3 s
Signal Velocity
2 × 108 m/s
102 m/s
Energy Dissipation
50 W
10 W
Precision
10−12
10−4
Failure Rate
< 10−9 /s
1/s
Fan Out Capacity
10
104
(cf., John von Neumann, The Computer and the Brain, Yale Univ. Press, New Haven, 1958.)
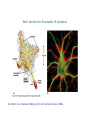
Different Kinds of Cells in a Nervous System
• Neurons process and transmit information.
– Golgi Type I neurons have long axons:
∗ Motor neurons (spinal cord, etc.)
∗ Pyramidal cells (cerebral cortex)
∗ Purkinje cells (cerebellum)
– Golgi Type II neurons have short axons.
∗ stellate cells (cerebral cortex)
• Glial Cells (maintain neurons)
Different Kinds of Neurons
From John E. Dowling, Neurons and Networks, 1992, p. 34.
Pyramidal Cells (Ramón y Cajal)
From http://neurolab.jsc.nasa.gov/cajal.htm
Purkinje Cell (Ramón y Cajal)
From http://neurolab.jsc.nasa.gov/cajal.htm
Visual Cortex of a Cat
From Gordon M. Shepherd, Neurobiology, 1988, p. 41.
Electron micrograph of a pyramidal cell
From Gordon. M. Shepherd, Neurobiology, 1988, p. 43.
Spiny Neuron on Glass
Photograph by Thomas Deerinck and Mark Ellisman (2009) from Carl Schoonover, Portraits of
the Mind, Abrams, New Yorik, 2010, p. 125.
A Motor Neuron
nucleus
axon hillock
soma
axon
dendrites
axon
terminals
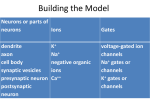
Cell Membranes
Each animal cell is enclosed by a membrane consisting of a thin lipid bilayer that isolates the
interior of the cell from its surroundings.
(B. Alberts et al., Molecular Biology of the Cell, Garland Science, NY, 2008.)
Proteins in the Membrane Perform Diverse Functions
• T ransporters actively transfer target molecules across the membrane:
– ionic pumps (e.g., the Na+ –K+ pump) maintain different ion concentrations inside
the cell (measured in millimoles per liter),
Outside neuron
Inside neuron
Na+
K+
Cl−
460
10
540
50
400
40
• Regulated channels passively allow the rapid flow of certain molecules across the
membrane:
– ionic channels regulated by neurotransmitters
– ionic channels regulated by voltage differences
– the acquaporin water channel, regulates the flow of H2 O across the memebrane.
– the NMDA-receptors allow Ca+2 to flow only if two conditions are satisfied: NMDA is
present, and the membrane is strongly depolarized (positive).
Equilibrium Potentials
Nernst’s Equation
E=
RT
[C]out
loge
,
nF
[C]in
where
R = 8.31 Joules/mole ◦ K
F = 9.65 × 104 Coulombs/mole
T = 18◦ C = 291◦ K
n = ionic charge
Thus,
E = (58 mV) log10
[C]out
[C]in
Goldman Equation
Vm
PK · [K+ ]out + PNa · [Na+ ]out + PCl · [Cl− ]in
RT
loge
=
= −70mV
F
PK · [K + ]in + PNa · [Na+ ]in + PCl · [Cl− ]out
Outside neuron
Inside neuron
Na+
K+
Cl−
460
10
540
50
400
40
(Concentrations measured in units of millimoles/liter. Recall, NA ≈ 6.022 × 1023 . From J.
Dowling, 1992, p. 72.)
Excitatory and Inhibitory Synapses
From John E. Dowling, Neurons and Networks, 1992, p. 50.
Each is about 1 µm in diameter, with a gap (or cleft) of about 20 nm.
Type I synapses are excitatory, enabling the absorption of sodium ions Na+ by the receiving
ligand-gated channel.
Type II synapses are inhibitory, enabling either the release of potassium ions K+ , or the
absorption of chloride ions Cl− .
Synapses can be either ionotropic (direct), or metabotropic (indirect).
Each neuron has thousands of synapses
(B. Alberts et al., Molecular Biology of the Cell, Garland Science, 2008.)
Principal Neurotransmitters
Amino acids
Biogenic amines
Neuropeptides
(fast: 1 – 20 msec)
(modulators: ∼ 1 sec)
(modulators lasting minutes)
Glutamate
Acetylcholine (ACh)
Substance P
Aspartate
Dopamine
Somatostatin
γ-amino-butyric acid (GABA)
Noradrenaline
Proctolin
Glycine
Serotonin
Neurotensin
Histamine
Luteinizing-hormone-releasing
hormone (LHRH)
(from Christof Koch, Biophysics of Computation, Oxford University Press, 1999, p. 93)
Numerous Dendritic Excitations =⇒ Action Potential
From Peter Dayan and L. F. Abbott, Theoretical Neuroscience, 2001, p. 6.
Three simulated recordings
From Peter Dayan and L. F. Abbott, Theoretical Neuroscience, 2001, p. 7.
Neuron Physiology
• Alan Hodgkin and Andrew Huxley measured the action potential of the squid giant axon,
and desribed the dynamics mathematically. Awarded the Nobel Prize in 1963 for this
work.
• Two types of electric potentials
– Synaptic/receptor potentials are graded, sustained and local. They are usually
stimulated by neurotransmitters. (The stronger the stimulus, the larger the
potential.) They add in an quasilinear manner.
– Action potentials, a transient spike that can propagate along the entire length of an
axon (1 mm to 1m.). All pulses have about the same amplitude (40 - 50 mV), and
same duration (about 1.5 ms). Each pulse is followed by a refractory period. Pulse
frequencies can vary.
• Electric potentials are caused by exchange of Na+ and K+ ions through the cell
membrane. (Na+ ions enter the neuron at the leading edge of the pulse. After a brief
delay, K+ ions leave the neuron, and restore electrical neutrality. Initial ion
concentrations are subsequently restored during the refractory period.)
• Spike trains enable a graded signal. (The production of a spike train involves a more
complex gate interaction.)
Measuring Action Potentials
From John E. Dowling, Neurons and Networks, 1992, p. 106.
A Neurophysiological Postulate
Let us assume then that the persistence or repetition of a reverberatory activity (or “trace”)
tends to induce lasting cellular changes that add to its stability. The assumption can be
precisely stated as follows: When an axon of cell A is near enough to excite a cell B and
repeatedly or persistently takes part in firing it, some growth process or metabolic change
takes place in one or both cells such that A’s efficiency, as one of the cells firing B is increased.
Donald O. Hebb, The Organization of Behavior, Wiley, New York, 1949, page 62.
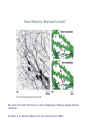
Neural Plasticity: What was for lunch?
New spines form within 30 minutes in a mouse hippocampus following repeated electrical
stimulation.
(B. Alberts et al., Molecular Biology of the Cell, Garland Science, 2008.)
The Hippocampus
Photograph by Thomas Deerinck and Mark Ellisman (2004) from Carl Schoonover, Portraits of
the Mind, Abrams, New Yorik, 2010, p. 103.
Blue Brain Project
The Blue Brain Project, Ecole Polytechnique Federale de Lausanne, Switzerland
http://bluebrain.epfl.ch
Computer science demands
abstractions!
McCulloch and Pitts (1943)
What is the computational capability of an idealized neural network?
Assume a simple MP neuron, with r excitatory and s inhibitory synapses:
x1
xr
xr+1
xr+s
k
y
Assume that xi ∈ {0, 1}, for i = 1, . . . , r + s. Define
1 if u ≥ 0
Θ(u) =
0 otherwise.
Then, the output y is
y = Θ
r
X
i=1
xi − k ·
s
Y
j=1
(1 − xr +j ).
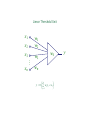
Linear Threshold Units (LTUs)
x1
x2
w1
w2
x3
w3
xn
wn
Σ
s
y
−
ϑ=–w0
The potential of the soma is approximated as weighted linear sum,
s = w · x = w1 x1 + w2 x2 + · · · + wn xn .
The output, is then given by
y = Θ(s − ϑ) = Θ
n
X
i=1
wi xi + w0
Linear Threshold Unit
x1
x2
w1
w2
x3
w3
xn
wn
w0
y = Θ
n
X
i=1
wi xi + w0
y
Higher-order Threshold Units
Quadratic Threshold Units
y = Θ
n X
n
X
i=1 j=i
(2)
wi,j xi xj +
n
X
wi xi + w0
i=1
Polynomial Threshold Units
Also known as sigma-pi units (Rummelhart et al., 1986):
y = Θ
n X
n
X
···
i1 =1 i2 =i1
n
X
(n)
wi1 ,...,in xi1 · · · xin +
in =in−1
n X
n
X
···
i1 =1 i2 =i1
n
X
(n−1)
wi1 ,...,in−1 xi1 · · · xin−1 + · · · +
in−1 =in−2
n
X
i1 =1
(1)
wi1 xi1 + w0
Feedforward Neural Netorks
x1
y1
x2
x3
y2
y3
xn
ym
Implements a mapping f : Rn → {0, 1}m . Network has n real-valued inputs: x1 , x2 , . . . , xn ,
and m binary outputs: y1 , y2 , . . . , ym .
Feedback Neural Network
u1
u2
–θ1
u3
–θ2
–θ3
w23
w1,1
y1 (t + 1)
y2 (t + 1)
= Θ w2,1
..
..
.
.
yn (t + 1)
wn,1
un
–θn
w32
w1,2
···
w2,2
..
.
···
...
wn,2
···
w1,n y1 (t) θ1
y2 (t) θ2
w2,n
.. .. − ..
. . .
wn,n
yn (t)
θn