Download EG/PH 305

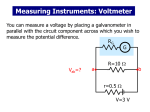
ENGR/PHYS 305
Electronics & Circuit Analysis I
Anthony Szpilka
Version 6/27/17
Lab 2. The d'Arsonval Meter and its Use as a Voltmeter
Purpose: The aim of this lab is to measure the characteristics of a typical d'Arsonval meter or
galvanometer, to determine how it may be employed as a voltmeter, and to investigate its
performance in that application.
Preliminary Reading
***** TO BE DONE BEFORE THE LAB SESSION *****
Read pp. A56-A58 of Barnaal’s Analog Electronics for Scientific Applications, for a brief
description of ammeters and voltmeters. Since any real galvanometer has a non-zero coil
resistance Rm , we will model it as an ideal (zero-resistance) meter M in series with Rm :
Rm
M
A
A
B
B
To use a galvanometer as an ammeter (i.e., to measure the current through some circuit
element), we must place the meter in series with the element, so that all the current that flows
through the element also flows through the meter:
i
ammeter
Rm
M
vs
+
RL
-
Provided the coil resistance Rm is much smaller than the rest of the circuit's resistance with
which it's in series (e.g., the load resistor R L in the diagram), the presence of the meter will not
change the "true" value of the current (i.e., the value of the current that flows through R L when
the meter is not present).
The maximum current this ammeter can measure (i.e., its "full-scale deflection current,"
i fs ) is typically quite small, maybe only i fs  1 mA . To measure larger currents, say up to
i  1 A , we can use a "shunt resistor" Rsh in parallel with the ammeter, to "bleed off" most of
the current (thus, we'd want i sh  999 mA when i  1 A , in this example):
ENGR/PHYS 305
Lab 2
Version 6/27/17
pg. 2 of 4
i sh
i
ammeter
Rsh
Rm
M
im
vs
RL
+
-
Refer to pp. A56-A57 of Barnaal for discussion of how the correct value for R sh is computed.
To use a galvanometer as a voltmeter, we could place a large resistor Rser in series
with the galvanometer, and then use the fact that full-scale deflection of the galvanometer
occurs when there is a total voltage of ( Rser  Rm )i fs across the galvanometer-plus- Rser
combination. This voltmeter must be placed in parallel with the circuit element across which we
wish to measure the voltage drop, so that the same voltage drop occurs across the element
and the voltmeter:
Rser
voltmeter
vs
+
-
Rm
RL
M
Refer to pp. A57-A58 of Barnaal to see how the correct value for Rser is computed. Provided
this resistance Rser is much larger than the circuit resistance with which the voltmeter is in
parallel (e.g., the load resistor R L in the diagram), the presence of the meter will not change
the "true" value of the voltage drop (i.e., the value of the voltage drop that occurs across R L
when the meter is not present).
Having seen the internal structure of an ammeter and a voltmeter, you should now
understand why the following Basic Rule of Electrical Circuits is true:
"Never put an ammeter in parallel with a circuit element;
never put a voltmeter in series with a circuit element!"
Don't forget this!
*****
*****
*****
ENGR/PHYS 305
Lab 2
Version 6/27/17
pg. 3 of 4
Procedure:
I. Modeling and Calibrating the d'Arsonval Meter
Record the number on the galvanometer you are using. Use your Fluke multimeter as
an ohmmeter to measure the coil resistance Rm for your galvanometer. Notice that the
galvanometer needle moves when you do this measurement: in your lab report, explain why!
The other parameter we need in order to characterize the galvanometer is its full-scale
deflection current, i fs . To measure this quantity, construct the following circuit, using a
resistance substitution box to get an accurate value for R.
WARNING:
Be sure to have R set at 20K and the power supply voltage knob turned all the way
DOWN before turning on the power--otherwise you might easily damage the
galvanometer.
R
20 K
vs
+
-
Rm
V
galvanometer
Fluke
M
Slowly turn the supply voltage up until the galvanometer needle is fully deflected (i.e., reading
"40"). From the voltage reading on the Fluke at this point, compute the current i fs that is
flowing through the galvanometer. As you now reduce the voltage back down to 0, check that
the galvanometer reading decreases linearly with the voltage drop: i.e., that you get 3/4 of fullscale deflection at 3/4 of the maximum voltage, 1/2 deflection at 1/2 the voltage, etc.
Now that you know the current i fs in amperes corresponding to a deflection of "40
units," you can determine how much current corresponds to each "unit" of deflection of the
galvanometer needle. Record this value.
II. d'Arsonval Meter as a Voltmeter
Since the ideal voltmeter draws no current through itself while measuring voltage, we
will try to approximate this situation with our galvanometer by placing a large resistance Rser in
series with it (as in the figure below). Since the galvanometer can measure currents no larger
than i fs , the maximum voltage drop we will be able to measure with this arrangement is
v fs  i fs ( Rser  Rm ) . From this relation, determine what size resistance Rser to use (from a
resistance substitution box) in order to obtain a convenient full-scale voltage capability of, say,
v fs  10 V . With the d'Arsonval meter employed in this arrangement as a voltmeter, what is
now the voltage corresponding to each "unit" of deflection of the needle?
ENGR/PHYS 305
Lab 2
Version 6/27/17
pg. 4 of 4
Rser
+
Rm
galvanometer
v
M
-
We can now use this "d'Arsonval voltmeter" (shown above) to measure voltage drops,
as in the simple circuit shown below. Unfortunately, since Rser  Rm is less than infinite, this
voltmeter will "load down" the voltage it is trying to measure, thus changing it, as you will now
investigate. Construct the following circuit, using a fixed carbon resistor in a wooden
component holder for R s , and measuring the actual value of R s before you insert it. Use
another resistance substitution box as the variable resistor R. Set the supply voltage v s to
10 V , measuring its value also.
Rs
Rser
A
2.2 K
vs
+
-
Rm
R
galvanometer
B
M
(a) Now increase R from 2 K to 10 K in 2 K steps, tabulating at each value the voltage
as read by your d'Arsonval voltmeter. (You should record the needle reading in "units" and then
convert that reading to the appropriate voltage value.) Then disconnect the d'Arsonval voltmeter
from the terminals A-B, and, using in its place the Fluke as a voltmeter, repeat the voltage
measurements for R = 2 K, 4 K, ... , 10 K.
(b) Change R s from 2.2 K to 10 K (measuring the new resistor before you install it, to
obtain its value accurately). Then repeat both series of voltage measurements as in (a) above
(i.e., first measuring with the d'Arsonval voltmeter, then with the Fluke), except this time vary R
from 10 K to 50 K in 10 K steps.
Post-Lab Data Analysis and Discussion:
1. What is the advantage of having an ideal voltmeter to measure voltage? Is it possible to
construct an ideal voltmeter? Why or why not?
2. Regarding the Fluke as an "ideal" voltmeter in the measurements you made for Part II
above, plot, as a function of R, both the actual (Fluke) voltage across R and the voltage you
measured with the d'Arsonval voltmeter. Plot both these functions on the same graph, but
make separate graphs for parts II(a) and II(b).
3. In these graphs, where is the discrepancy between "measured" (d’Arsonval) and "actual"
(Fluke) voltage the worst? Why is the error greater in these ranges than in the others?
Account quantitatively for the discrepancy you see, by computing the values you would
theoretically expect for the Fluke voltage measurements, and for the d’Arsonval voltages.
Record in your lab report the equations you use in each case. Tabulate these theoretical
voltages next to your tabulated experimental voltages. Check your calculations by
completing the WebAssign “Lab 2” table (include a copy of it in your final lab report).