Download Math 111 Pre-test(Show all work

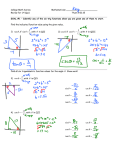
Math 111 Pre-test
Show all work. No calculators. No books. Take as much time as you like but do it NEATLY!!
To be handed in first day of class.
This will NOT count toward your grade.
1. Find the area of the region bounded by
2. Find the equation of the line with slope 2
that intersects the x-axis where x=3.
y  x  3 , the x-axis, x=3 and x=5.
3. The parabola y  x 2 has slope 6 at the point
(3, 9). Thus, the tangent line to the curve at
this point has slope 6. Find all points where
the line perpendicular to this tangent line
(through (3, 9)) intersects the parabola.
5. Let y  f ( x)  x 2  1 . Find f (0), f (2) ,
f (3  h)  f (3)
(simplify).
h
7. Evaluate f (3), f (1), f (1) and f (3) if
f (3  h), and
f ( x) 
9. Find the inverse of: f ( x) 
x2
3x  5
y  4  ( x  3) 2 ;
1
4  ( x  3) 2  ;

4
1
2
y  ( x  3) 2 ; y  4   2( x  3)  ;
4
x3  4 x 2  3x
13. Find the roots of f ( x) 
( x  2)( x  4)2
y

3
numerator.
f ( x)  x 2  1 on x  3
g ( x)  2ax on x  3
12. A right circular cone has slant height
(distance from top point to any point on
the base) of 3 units. Write the volume of
this cone as a function of the height
only.

and all values of x where the function lies
above the x-axis.
15. Sketch y   sin(2 x) on 2  x  2
17. Find the area of the square:
7
9h 3
. Rationalize the
h
and f and g meet at x=3, find a.
10. Find the remainder when
x3  6 x 2  2 x  4 is divided by x 2  2
11. Sketch the set of graphs by building up from
the first and using scaling and translations:
(label vertex & intercepts)
y  ( x  3) 2 ;
6. Consider
8. If
3x 2  2
.
x2
y  x2 ;
1
. Find f (1), f ( 5) ,
x6
f (2  h)  f (2)
f (2  h), and
(simplify)
h
4. Let y  f ( x) 
14. Find all values of x satisfying x  3  4
both algebraically and graphically and
explain what the region means in terms of
distance.
16. Solve for x: 2 ln( x  3)  ln( x  15)  ln 3
18. An open top box is constructed from a
rectangular piece of cardboard with
dimensions 14 in by 22 in by cutting equal
squares with side x from the corners and
folding the sides up. Express the volume of
the resulting box in terms of x.
While the following list is not exhaustive, it is STRONGLY recommended that you
deeply know these topics BEFORE the first day of class:
 Trigonometry:
 Values of sin, cos, tan, sec, csc, and cot for 0,
    2 3 5
and  radians and so on.
6, 4 3, 2, 3, 4, 6,
 Basic trigonometric identities and concepts
o Finding values of sin, cos, tan, sec, csc, and cot given right triangles.
o Finding values of inverse trig functions given right triangles.
o Understanding the unit circle, where each trig function is +/o Addition formulas, double angle and half-angle formulas
o Relationship between degrees and radians and converting from one to the
other
o Relationship among the various trig functions; finding one from the others
o Inverse trig functions
o Law of sines and law of cosines
o Reasoning based on similar triangles
o Evaluating expressions involving trig and inverse trig functions, e.g.
4

cos  sin 1 
5


Formulas for area and perimeter of a circle, triangle, rectangle and square; volume of
a cube, sphere, rectangular prism, cylinder and cone; length of sector of a circle,
circumference of a circle;

Basics
 Fluency with arithmetic and algebraic skills, including:
o Adding, subtracting, multiplication, division and commutative, associative
and distributive laws for numbers and expressions
o Rational/fractional functions and expressions and rationalizing numerators
and denominators
o Powers – especially under roots or fractional, and powers to powers,
EXPONENTS! Also, absolute value.
 Simplifying expressions –
o alternate representations
o polynomial, rational, trigonometric, powers (including fractional powers)
o factoring, especially x 2  y 2 and x3  y 3
 Order of operations
 Unit conversion

Solving equations and functions
 Solving one and two dimensional systems of linear equations
 Solving linear inequalities







Solving quadratic equations – quadratic formula, finding roots, completing the
square
Equation of lines (point-slope; slope intercept) and normal (perpendiculars);
midpoint of a line segment
Shapes of curves – monomials, ln, exponentials, sin, cos, tan, formula for a circle,
parabola, ellipse, hyperbola
Mapping functions (shifting and scaling)
Symmetry
Properties of logarithms, manipulating using logarithms, change of base
Function notation

Key formulas and how to use them
 Pythagorean theorem, distance formula
 Quadratic formula
2
2
 sin x  cos x  1 and the related formulas for tan, sec, cot and csc that can be
derived from these

Curves (functions) representing the following expressions:
y=sin x, cos x, tan x, sec x, csc x, and cot x, ex, 2x, e-x, x2, x3, x4, x-1, x-2, |x|, ln(x).

Difference between zero and infinity.
Understanding when 0 or infinity is in the denominator.

The key rules of logarithms:
y  log a x means a y  x
log a  log b  log(ab); log a  log b  log( a / b)
log ab  b log a
a loga x  x; log a a x  x

Turning words/sentences into equations/expressions