Download Given the equation, , there are several solutions (several angles with

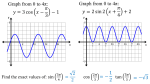
MA 15400
Lesson 12
Trigonometric Equations
Section 7.2
1
Given the equation, sin x  , there are several solutions (several angles with a sine value of ½ ).
2
When solving such an equation you may be asked to only find solutions in a given interval. If asked
to find all real solutions, you will have to write an expression to represent such solutions. (This is
the 'new part' of today's lesson.) To represent these infinite solutions, we will use n to represent an
arbitrary integer.
Find all solutions of the equation.
a) Interval [0, 2)
b) All Real Numbers
1
2
 7
a) x  ,
(Q I and IV)
4 4
cos x 
sin t  
1
2
b) The period of the cosine is 2π.
Any coterminal angles would also
be solutions.

7
x   2n,
 2n
4
4
n = ...-2, -1, 0, 1, 2, ...
cot   
1
3
tan  
1
3
b) The period of the
tangent is π.
csc  2
sec    2

1
MA 15400
Lesson 12
Trigonometric Equations
cosu  1
* sin x 
4
5
Section 7.2
tan  is undefined
Find all the solutions of the equation. [You are to solve for the variable.]
1
cos 2 
2 sin 3h  2 (Isolate the function first.)
2

5
2   2n 2 
 2n
3
3
Divide each term (both sides) by 2



6

6
 n
 n ,

5
 n
6
5
 n
6
3 sec(5t )  2  0
tan( 7 x)  1

1 
3 cot  t   1
4 

  1
cos4x  

6  2
cot 4   3  0
2
MA 15400
Lesson 12
Trigonometric Equations
1
2
(Take positive/negative square roots)
cos 2 x 
Section 7.2
2 sin t  1cos t  0
(Always give simplest answer)
3 csc 2   4  0
3 tan 2 4  1  0
3