* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Phase Frequency Detector Principles
Switched-mode power supply wikipedia , lookup
Radio direction finder wikipedia , lookup
Regenerative circuit wikipedia , lookup
Resistive opto-isolator wikipedia , lookup
Power electronics wikipedia , lookup
Mechanical filter wikipedia , lookup
Integrating ADC wikipedia , lookup
Immunity-aware programming wikipedia , lookup
Opto-isolator wikipedia , lookup
Direction finding wikipedia , lookup
Valve RF amplifier wikipedia , lookup
Distributed element filter wikipedia , lookup
Audio crossover wikipedia , lookup
Radio transmitter design wikipedia , lookup
Equalization (audio) wikipedia , lookup
Index of electronics articles wikipedia , lookup
Bellini–Tosi direction finder wikipedia , lookup
Linear filter wikipedia , lookup
Rectiverter wikipedia , lookup
Wien bridge oscillator wikipedia , lookup
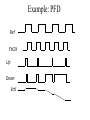
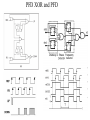
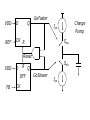
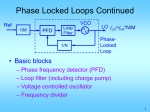
PLL Sub System3 • Phase Frequency Detector (PFD) • The Charge pump principles and Realizations • The loop filter realizations • Targil3: PLL Design Cont . Phase Frequency Detector Principles The schematic of the PFD is given here. Its output depend both on phase and frequency of the inputs. It compares the leading edge of the data (clkref) and dclock. Thus both must be present to the PFD, Yet their respective widths play no roll. Operation: if the rising edge of data leads the rising edge of dclock the ‘up’ signal of the pfd goes high while the ‘down’ signal goes low. At the opposite scenario, where dclock rising edge leads data rising edge lead the ‘up’ signal will go low and the ‘down’ signal will assert high. Consequently dclock frequency will increases/ decreased to bring its rising edge closer to data rising edge. When both rising edge coincide the pll is in lock and note that then (unlike the xor PD), both ‘up’ and ‘down’ outputs remain low. Phase Frequency Detector Principles Again, we will characterize the PFD behavior. • A rising edge from both dclock and data must be present when doing phase comparison. • The width of dclcok and data is irrelevant. • The output ‘Up’ and ‘Down’ are both low at lock eliminating ripple on the output of the loop filter. • The PFD has poor immunity, any false edge will affect PFD output Phase Frequency Detector Principles Again, we will characterize the PFD behavior. • A rising edge from both dclock and data must be present when doing phase comparison. • The width of dclock and data is irrelevant. • The output ‘Up’ and ‘Down’ are both low at lock eliminating ripple on the output of the loop filter. • The PDF PLL will not lock on harmonics (‘relaxed VCO design) • Perfect’ clock duty cycle is not a must (rising edges is the factor) • The PFD has poor immunity, any false edge will affect PFD output Phase Frequency Detector Principles The output of the PFD should be combined into a single output driving the loop filter. There are two main methods of doing it: tri_state output and Charge pump output. With tri_state method the (up/down) switches are directly connected to VCC/VSS respectively ( w/o the current sources). When up and down are low (lock) the driver is in tri_state. The main problem with the tri_state methods is its sensitivity to supply and Gnd Noise and variations. As current source is ‘independent’ of that noise the modulated VCO has better supply noise immunity (note that This feature was ‘built in’ with the XOR methods due to its averaging. PFD Logic States • 3 and “1/2” Output states • States: Up 0 0 1 1 Down 0 1 0 1 Effect: No Change Slow Down Speed Up Avoid Dead-Zone Example: PFD Ref FbClk Up Down Vctl Avoiding the Dead-Zone • “Dead-zone” occurs when the loop doesn’t respond to small phase errors - e.g. 10 pS phase error at PFD inputs: – PFD cannot generate 10 pS wide Up and Down pulses – Charge-pump switches cannot turn on and off in 10 pS – Solution: delay reset to guarantee min. pulse width (typically > 150 pS) Adding Delay to PFD reset Vdd D GoFaster Q DFF Ref CK R DLY Vdd R D Q DFF FB CK GoSlower PFD XOR and PFD Charge Pump • Converts PFD phase error (digital) to charge (analog) • Charge is proportional to PFD pulse widths Qcp = Iup*tfaster – Idn*tslower • Qcp is filtered/integrated in low-pass filter VDD D Q REF CK R GoFaster Charge Pump Icp Sup Reset VDD R D DFF FB CK Sdn Q GoSlower Icp Charge-Pump Wish List • Equal UP/DOWN currents over entire control voltage range - reduce phase error. • Minimal coupling to control voltage during switching - reduce jitter. • Insensitive to power-supply noise and process variations – loop stability. • Easy-to-design, PVT-insensitive reference current. • Programmable currents to maintain loop dynamics (vs. M, fref)? • Typical: 1A (mismatch)< Icp < 50 A (Vctl) Static Phase Error and CP Up/Down Mismatches • Static Phase Error: in lock, net UP and DOWN currents must integrate to zero – If UP current is 2X larger, then DOWN current source must be on 2X as long to compensate – Feedback clock must lead reference for DOWN to be on longer – Terr = Tdn - Tup = Treset * (Iup/Idn – 1) Static Phase Error and CP Up/Down Mismatches • Phase error can be extremely large at low VCO frequencies (esp. if self-biased) due to mismatch in current mirrors (low Vgs-Vt) • Increase Vgs or decrease Vt (large W*L) • Typical static phase error < 100 pS Simple Charge Pump • R(switches) varies with Vctl due to body-effect • Use CMOS pass-gate switches for less Vctl sensitivity • Long-channel current sources for matching and higher Rout m4 m3 Ibias Up_n Down m1 m2 m5 Vctl m6 m7 Charge Pump: const I with amp & TG’s • Amp keeps Vds of current sources constant (Young ’92) • Amp sinks “waste” current when UP, DOWN off Vbp Add cap to VirtVctl for volt. stability Up Vctl Up_n + - Down VirtVctl Down Down_n Vbn Up Amp Ibias should track Icp PFD Loop Filter For both tri_state and Charge pump outputs we want the loop filter to behave like integrator for slow variation of the phase difference that is averaging the PFD output. For fast variation we want to minimize the averaging in order to track fast variations in phase difference between the rising edges. Looking at the charge pump loop filter we c that Ipump linearly charges both C1,C2 capacitors at slow variations, This gives the averaging effect, yet at fast variation it drives R1 (assuming C2 is small ) , eliminating the averaging effect and allowing the VCO to tack quick changes in input data Targil :find transfer function of the charge pump loop filter (Vout/Iin). Low-Pass Loop Filter • Integrates charge-pump current onto C1 cap to set average VCO frequency (“integral” path). • Resistor provides instantaneous phase correction w/o affecting avg. freq. (“proportional” path). • C2 cap smoothes large IR ripple on Vctl • Typical value: 0.5k < Rlpf < 20kOhm Vctl Res C1 C2 Low-Pass Filter Smoothing Cap(C2) • “Smoothing” capacitor on control voltage filters CP ripple, but may make loop unstable • Creates parasitic pole: p = 1/(R C2) • C2 < 1/10*C1 for stability • C2 > 1/50*C1 for low jitter • Smoothing cap reduces “IR”-induced VCO jitter to < 0.5% from 5-10% • fvco = KvcoIcpTerr/C2 • Larger C2/C1 increases phase error slightly Low-Pass Filter Capacitors • At <= 130nm, thin-gate oxide leakage is huge: – – – – Ileak ~ Vgate 4.5 NMOS leakier than PMOS Weak temperature dependence Ileak vs. tox ~2-3X per Angstrom • Use metal caps or thick-gate oxide caps to reduce leakage • Metal caps use 10X more area than thin gate caps – Use minimum width/spacing parallel lines – Hard to LVS - Check extracted layout for correct connectivity Low-Pass Filter Capacitors • Even thick gate oxide may still leak too much • Large filter cap (C1) typically ranges from 50pF to 400 pF • C1 cap BW may be low as ~10X PLL BW for nearly ideal behavior • Min C2 BW set by Tref • Cap BW ~ 1/RC ~ 1/L2 • Gate cap not constant with Vgs • Loop filter ‘Calculator’: http://geocities.com/fudinggepll/pllfilterprogram.html PLL Loop Eqns: Limits on Rlpf • Parasitic LPF Pole: Rlpf*C2 ~ Tref/ if we want V(C1) ~ V(C2) by end of Tref (goal) (Maneatis ISSCC ’03) I = (Vc2 –Vc1)/R = Cv/dt =>Cv/t = v/R Vctl \\ t= I C1 C2 RC2 • Also, for Damping Factor: usually 0.45 < < ~1.5 , From loop eqns, we saw: = ½ (Rlpf * C1 * n )-1 More on PLL PLL Loop Filter parameters: Loop Type and Order Loop Filter Design and Matlab loop Analysis Passive/Active Loop topologies Impact of open loop parameters variations Impact on open loop parasitic Poles and Zeros variations PLL noise (and Jitter..) performance CDR (Clock Data Recovery) • Loop filter ‘Calculator’: http://geocities.com/fudinggepll/pllfilterprogram.html