Download Phase Frequency Detector Principles

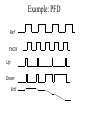
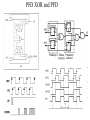
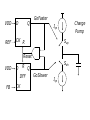
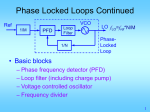
PLL Sub System3
• Phase Frequency Detector (PFD)
• The Charge pump principles and Realizations
• The loop filter realizations
• Targil3: PLL Design Cont
.
Phase Frequency Detector Principles
The schematic of the PFD is given here. Its output depend both on phase
and frequency of the inputs. It compares the leading edge of the data
(clkref) and dclock. Thus both must be present to the PFD, Yet their
respective widths play no roll.
Operation: if the rising edge of data leads the rising edge of dclock the
‘up’ signal of the pfd goes high while the ‘down’ signal goes low. At
the opposite scenario, where dclock rising edge leads data rising edge
lead the ‘up’ signal will go low and the ‘down’ signal will assert high.
Consequently dclock frequency will increases/ decreased to bring its
rising edge closer to data rising edge. When both rising edge coincide
the pll is in lock and note that then (unlike the xor PD), both ‘up’ and
‘down’ outputs remain low.
Phase Frequency Detector Principles
Again, we will characterize the PFD behavior.
• A rising edge from both dclock and data must be present when
doing phase comparison.
• The width of dclcok and data is irrelevant.
• The output ‘Up’ and ‘Down’ are both low at lock eliminating
ripple on the output of the loop filter.
• The PFD has poor immunity, any false edge will affect PFD output
Phase Frequency Detector Principles
Again, we will characterize the PFD behavior.
• A rising edge from both dclock and data must be present when
doing phase comparison.
• The width of dclock and data is irrelevant.
• The output ‘Up’ and ‘Down’ are both low at lock eliminating
ripple on the output of the loop filter.
• The PDF PLL will not lock on harmonics (‘relaxed VCO design)
• Perfect’ clock duty cycle is not a must (rising edges is the factor)
• The PFD has poor immunity, any false edge will affect PFD output
Phase Frequency Detector Principles
The output of the PFD should be combined into a single output driving
the loop filter. There are two main methods of doing it: tri_state
output and Charge pump output. With tri_state method the (up/down)
switches are directly connected to VCC/VSS respectively ( w/o the
current sources). When up and down are low (lock) the driver is in
tri_state. The main problem with the tri_state methods is its sensitivity
to supply and Gnd Noise and variations. As current source is
‘independent’ of that noise the modulated VCO has better supply noise
immunity (note that This feature was ‘built in’ with the XOR methods
due to its averaging.
PFD Logic States
• 3 and “1/2” Output states
• States:
Up
0
0
1
1
Down
0
1
0
1
Effect:
No Change
Slow Down
Speed Up
Avoid Dead-Zone
Example: PFD
Ref
FbClk
Up
Down
Vctl
Avoiding the Dead-Zone
• “Dead-zone” occurs when the loop doesn’t
respond to small phase errors - e.g. 10 pS
phase error at PFD inputs:
– PFD cannot generate 10 pS wide Up and Down
pulses
– Charge-pump switches cannot turn on and off in
10 pS
– Solution: delay reset to guarantee min. pulse
width (typically > 150 pS)
Adding Delay to PFD reset
Vdd
D
GoFaster
Q
DFF
Ref
CK
R
DLY
Vdd
R
D
Q
DFF
FB
CK
GoSlower
PFD XOR and PFD
Charge Pump
• Converts PFD phase error (digital) to charge
(analog)
• Charge is proportional to PFD pulse widths
Qcp = Iup*tfaster – Idn*tslower
• Qcp is filtered/integrated in low-pass filter
VDD
D
Q
REF
CK R
GoFaster
Charge
Pump
Icp
Sup
Reset
VDD
R
D
DFF
FB
CK
Sdn
Q
GoSlower
Icp
Charge-Pump Wish List
• Equal UP/DOWN currents over entire control
voltage range - reduce phase error.
• Minimal coupling to control voltage during
switching - reduce jitter.
• Insensitive to power-supply noise and process
variations – loop stability.
• Easy-to-design, PVT-insensitive reference
current.
• Programmable currents to maintain loop
dynamics (vs. M, fref)?
• Typical: 1A (mismatch)< Icp < 50 A (Vctl)
Static Phase Error and CP
Up/Down Mismatches
• Static Phase Error: in lock, net UP and DOWN
currents must integrate to zero
– If UP current is 2X larger, then DOWN current
source must be on 2X as long to compensate
– Feedback clock must lead reference for DOWN to
be on longer
– Terr = Tdn - Tup = Treset * (Iup/Idn – 1)
Static Phase Error and CP
Up/Down Mismatches
• Phase error can be extremely large at low VCO
frequencies (esp. if self-biased) due to mismatch
in current mirrors (low Vgs-Vt)
• Increase Vgs or decrease Vt (large W*L)
• Typical static phase error < 100 pS
Simple Charge Pump
• R(switches) varies with Vctl due to body-effect
• Use CMOS pass-gate switches for less Vctl
sensitivity
• Long-channel current sources for matching
and higher Rout
m4
m3
Ibias
Up_n
Down
m1
m2
m5
Vctl
m6
m7
Charge Pump: const I with amp &
TG’s
• Amp keeps Vds of current sources constant
(Young ’92)
• Amp sinks “waste” current when UP, DOWN
off
Vbp
Add cap to VirtVctl for volt. stability
Up
Vctl
Up_n
+
-
Down
VirtVctl
Down
Down_n
Vbn
Up
Amp Ibias should track Icp
PFD Loop Filter
For both tri_state and Charge pump outputs we want the loop filter to
behave like integrator for slow variation of the phase difference
that is averaging the PFD output. For fast variation we want to
minimize the averaging in order to track fast variations in phase
difference between the rising edges. Looking at the charge pump loop
filter we c that Ipump linearly charges both C1,C2 capacitors at slow
variations, This gives the averaging effect, yet at fast variation it drives
R1 (assuming C2 is small ) , eliminating the averaging effect and
allowing the VCO to tack quick changes in input data Targil :find
transfer function of the charge pump loop filter (Vout/Iin).
Low-Pass Loop Filter
• Integrates charge-pump current onto C1 cap to
set average VCO frequency (“integral” path).
• Resistor provides instantaneous phase correction
w/o affecting avg. freq. (“proportional” path).
• C2 cap smoothes large IR ripple on Vctl
• Typical value: 0.5k < Rlpf < 20kOhm
Vctl
Res
C1
C2
Low-Pass Filter Smoothing Cap(C2)
• “Smoothing” capacitor on control voltage filters
CP ripple, but may make loop unstable
• Creates parasitic pole: p = 1/(R C2)
• C2 < 1/10*C1 for stability
• C2 > 1/50*C1 for low jitter
• Smoothing cap reduces “IR”-induced VCO
jitter to < 0.5% from 5-10%
• fvco = KvcoIcpTerr/C2
• Larger C2/C1 increases phase error slightly
Low-Pass Filter Capacitors
• At <= 130nm, thin-gate oxide leakage is huge:
–
–
–
–
Ileak ~ Vgate 4.5
NMOS leakier than PMOS
Weak temperature dependence
Ileak vs. tox  ~2-3X per Angstrom
• Use metal caps or thick-gate oxide caps to reduce
leakage
• Metal caps use 10X more area than thin gate caps
– Use minimum width/spacing parallel lines
– Hard to LVS - Check extracted layout for correct
connectivity
Low-Pass Filter Capacitors
• Even thick gate oxide may still leak too much
• Large filter cap (C1) typically ranges from 50pF to
400 pF
• C1 cap BW may be low as ~10X PLL BW for nearly
ideal behavior
• Min C2 BW set by Tref
• Cap BW ~ 1/RC ~ 1/L2
• Gate cap not constant with Vgs
• Loop filter ‘Calculator’:
http://geocities.com/fudinggepll/pllfilterprogram.html
PLL Loop Eqns: Limits on Rlpf
• Parasitic LPF Pole: Rlpf*C2 ~ Tref/ 
 if we want V(C1) ~ V(C2) by end of Tref (goal)
(Maneatis ISSCC ’03)
I = (Vc2 –Vc1)/R = Cv/dt
=>Cv/t = v/R
Vctl
\\
t=
I
C1
C2
RC2
• Also, for Damping Factor: usually 0.45 <  < ~1.5 ,
From loop eqns, we saw:   = ½ (Rlpf * C1 * n )-1
More on PLL
PLL Loop Filter parameters: Loop Type and Order
 Loop Filter Design and Matlab loop Analysis
 Passive/Active Loop topologies
 Impact of open loop parameters variations
 Impact on open loop parasitic Poles and Zeros variations
 PLL noise (and Jitter..) performance
 CDR (Clock Data Recovery)
• Loop filter ‘Calculator’:
http://geocities.com/fudinggepll/pllfilterprogram.html