Download IB Math Analysis

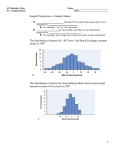
Group Members:
IB Statistics
Activity 9A: Intro to Sampling Distributions
The heights (in inches) of young women follow the N(64.5, 2.5) distribution. The random
variable X is the height of a randomly selected young woman. In this activity, you will
use GDC to randomly sample from this distribution and then use post-it notes to construct
a distribution of averages.
1. What is the mean μ for this population?
2. What is standard deviation σ for this population?
3. What is the variance σ2 for this population?
If we choose one woman at random, the heights we get in repeated choices follow the
N(64.5, 2.5) distribution. On GDC, go into the statistics/list editor and clear list 1 (L1).
Simulate the heights of 100 randomly selected young women and store these heights in
L1 as follows:
 Highlight L1 with your cursor.
 Press MATH, choose PRB, choose randNorm.
 Complete the command randNorm(64.5, 2.5, 100).
 Press Enter.
4. Plot a histogram of the 100 heights as follows. Deselect active functions in the Y =
window, and turn off all STAT PLOTS. Set WINDOW dimensions to Xmin = 57,
Xmax = 72, Xscl = 2.5, Ymin = – 10, Ymax = 45, Yscl = 5 to extend 3 standard
deviations to either side of the mean, 64.5. Define Plot 1 to be a histogram using the
heights in L1. Press GRAPH to plot the histogram. Sketch and label what you see:
5. Describe the approximate shape of your histogram. Is it fairly symmetric or is it
clearly skewed?
6. Approximately how many heights should there be within 3σ of the mean (that is,
between 57 and 72)? Use TRACE to count the number of heights within 3σ.
7. Approximately how many heights should there be within 1σ of the mean? Within 2σ
of the mean? Again use TRACE to find these counts, and compare them with the
numbers you would expect.
8. Use 1-Var Stats to find mean, median, and standard deviation for your data. Compare
the sample mean (x-bar) with µ. What do you notice?
9. Compare the sample standard deviation s with σ. What do you notice?
10. Recall that the closer the mean and the median are, the more symmetric the
distribution. How do the mean and median for your 100 heights compare?
11. Define Plot 2 to be a boxplot using L1, and then press GRAPH again. The boxplot
will be plotted above the histogram. Does the boxplot appear symmetric?
12. How close is the median in the boxplot to the mean of the histogram?
13. Based on the appearance of the histogram and the boxplot, and a comparison of the
mean and median, would you say that the distribution is nonsymmetric, moderately
symmetric, or very symmetric?
14. Repeat the process of taking another sample, using randNorm (64.5, 2.5, 100) at least
3 more times. For each sample, record the mean (x-bar), median, and standard
deviation s on the next page.
Sample #2:
Mean:
Median:
Standard Deviation:
Sample #3:
Mean:
Median:
Standard Deviation:
Sample #4:
Mean:
Median:
Standard Deviation:
In large print, write the mean (x-bar) for each sample on a different post-it note. Next, we
will build a post-it note histogram of the distribution of the sample mean (x-bar). There
will be and x-axis drawn on the board to indicate the different mean heights. When
instructed, go to the board and stick each of your post-it notes directly above the tick
mark that is closest to the mean written on the note. When post-it note histogram is
complete, answer the following questions:
15. What is the approximate shape of the sampling distribution of x-bar?
16. Where is the center of the sampling distribution of x-bar?
17. How does this center compare with the mean of heights of the population of all young
women?
18. Roughly, how does the spread of the sampling distribution of x-bar compare with the
spread of the original distribution (σ = 2.5)?
19. While someone calls out the values of x-bar from the post-it notes, enter these values
into L2 in GDC. Turn off Plot 1 and define Plot 3 to be a boxplot of the x-bar data
from the post-it note histogram. How do the distributions of X and x-bar compare
visually?
20. Use 1-Var Stats to calculate the standard deviation sx-bar for the distribution of x-bar.
Compare this value with 2.5/(sq. rt. 100) = 0.25.
21. Fill in the blanks in the following statement with a function of µ or σ.
“The distribution of x-bar is approximately Normal with mean μx-bar =
and standard deviation σ x-bar =
.”