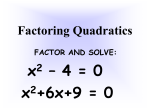Download Factoring Using The Diamonds Name

Factoring Using The Diamonds
Your task is to fill in each diamond with the two numbers that multiply to give the
number at the top and also add to give the number at the bottom.
20
4
Name ________________________________________
5
See the example to the left. The answer is 4 and 5 because 4*5 = 20 and 4 + 5 = 9
9
Part I
1.
2.
3.
4.
5.
36
7
6
2
72
12
8
7
3
17
6.
7.
8.
9.
10.
44
63
64
75
50
24
24
20
28
27
Part II
11.
12.
13.
14.
15.
2
12
21
5
1
–3
–8
–10
–6
–2
16.
17.
18.
19.
20.
24
30
18
4
14
–11
–13
–11
–5
–9
21.
22.
23.
24.
25.
49
36
30
36
40
–14
–12
–11
–15
–13
Part III
26.
27.
28.
–45
–33
–4
8
31.
32.
29.
30.
–10
–28
–16
3
–3
6
33.
34.
35.
–24
–48
–2
–2
–8
–2
8
–1
1
2
36.
37.
–15
2
38.
39.
40.
–200
–45
–60
–60
10
12
–7
11
Part IV
41.
42.
43.
44.
45.
45
45
–45
–45
45
14
–14
4
–4
18
46.
47.
48.
49.
50.
60
–70
–56
–10
–10
23
3
1
9
–9
51.
52.
53.
54.
–16
–25
–36
0
0
0
55.
–36
120
9
22
Factoring Trinomials
x2 + bx + c
x2 + 5x + 6 = (x + 2)(x + 3)
6
2
3
5
c
2
When factoring a trinomial, x + bx + c
the “diamond” is set up
b
c
the two “Magic numbers”, m and , are used to find the two binomials. (x + m)(x + n)
3
Example 1: x2 + 4x + 3
x2 + 3x + 1x + 3
(x + 3)(x + 1)
multiply to give 3
3
m
n
b
1
4
Add to get 4
8
multiply to give 8
2
Example 2: x + 6x + 8
x2 + __ x + __x + 8
(x + ___)(x + ___ )
1:
6
Add to get 6
x2 + 8x + 15
2:
x2 + 3x – 10
x2 + __ x + __x + 15
x2 + __ x + __x – 10
(x + ___)(x + ___)
(x + ___)(x + ___)
3. x2 + 2x – 48
4. x2 – 7x – 30
5. x2 – 13x + 40
6. x2 – 11x + 18
7. x2 – 6x + 9
8. x2 – 11x – 42
9. x2 + 9x – 70
10. x2 + 16x + 39
10. x2 + 2x – 15
11. x2 – 10x + 25
12. x2 + 5x – 2
13. x2 + 8x + 16
14. x2 – 11x + 28
15. x2 – 7x + 10
16. x2 + 4x + 4
17. x2 + 5x – 14
18. x2 – 12x + 36
19. x2 – 6x + 9
20. x2 – 9x + 14
21. x2 – 8x + 15
22. x2 – 4x – 45
23. x2 – 3x – 28
24. x2 – 2x – 99
25. x2 – 7x – 60
Factoring Trinomials
ax2 + bx + c
Now there is a leading coefficient greater than 1 in front of the x2 term.
First let’s multiply out two binomials. (2x + 5)(x + 2)
2x2 + 4x + 5x + 10
2x2 + 9x + 10
Our two middle terms are 4x and 5x.
Now let’s reverse our steps and use the diamond to factor.
2 ∙ 10 = 20
Since the 2 in front of the x2 is going to affect
our middle term, it has to be included in the
diamond. 2 ∙ 10 = 20
20
2x2 + 9x + 10
4
5
9
So 2x2 + 9x + 10 becomes
What 2 numbers multiply to 20 and add to 9?
4 ∙ 5 = 20 and 4 + 5 = 9
2x2 + 4x + 5x + 10
Now we need to create two binomials that will multiply to be
2x2 + 4x + 5x + 10
We know that 2x2 is made by multiplying 2x
(2x ____ )(x ____ )
by x
To get the middle terms of 4x and 5x
we need to multiply the 2x by something to make 4x and
the x by something to make 5x.
4x
(2x ___ )(x ___ )
5x
By filling in the missing numbers you get.
(2x + 5)(x + 2)
Always check to make sure you get the correct end term.
5 ∙ 2 = 10
Example 2: 3x2 + 14x + 15
3 ∙ 15 = 45
Since the 3 in front of the x2 is going to affect
our middle term, it has to be included in the
diamond. 3 ∙ 15 = 45
45
3x2 + 14x + 15
9
5
14
So 3x2 + 14x + 15 becomes
What 2 numbers multiply to 45 and add to 14?
9 ∙ 5 = 20 and 9 + 5 = 14
3x2 + 9x + 5x + 45
Now we need to create two binomials that will multiply to be
3x2 + 9x + 5x + 45
We know that 3x2 is made by multiplying 3x
(3x ___ )(x ___ )
by x
To get the middle terms of 9x and 5x
we need to multiply the 3x by something to make 9x and
the x by something to make 5x.
9x
(3x ___)(x
___)
5x
By filling in the missing numbers you get.
(3x + 5)(x + 3)
Always check to make sure you get the correct end term.
5 ∙ 3 = 15