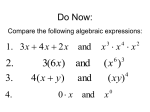Download Number 9 - Combining Exponent Laws_1

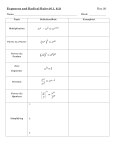
Math 10C
Real Numbers: Lesson #9
Combining Exponent Laws
Objective: By the end of this lesson, you will be able to:
- Apply exponent laws to expressions with negative and fraction exponents.
We can also apply the exponent laws to negative and rational exponents. To simplify algebraic
expressions, it is convention to write all powers with a _______________, _________________
exponent.
Negative Exponents
e.g. 1) Use exponent laws to write
 43  44
 42
as a single power, then evaluate.
When there is a negative exponent on a variable, move it to the _______________________ and
make the exponent _________________.
e.g. 2) Simplify the following expressions:
a)
c)
m n 
6 x 5 y 3
b)
14 x 2 y
s 5 t 2
 4 xy5 
d)  7 5 
x y 
5
 2 3
s t 
3 1 3
2
Math 10C
Real Numbers: Lesson #9
Rational Exponents
Fractions Review:
 To multiply fractions:
20 1
 
3 5
e.g. 3)

To add or subtract fractions:
5 3
 
6 8
e.g. 4)

We will leave all fractions as ________________ ______________.
e.g. 5) Write as a single power, then evaluate:
a)
2.5
2.5
5
3
2
3
3
2
b) 4  4 2
e.g. 5) Write each expression as a single power with positive exponents and then as a radical:
 
5
a) y 3
1
4
1
b) x 2  x
 34
Math 10C
Real Numbers: Lesson #9
 3  32  1 12 
c)  a b  a b 




 100 x
d) 
1
 25 x5 y  2






1
2
e.g. 4) Write each radical as a single power and then as a single radical.
a)
4
x7
b)
Assignment: Exponents Assignment
Further Practice: p. 242-243 #8-11, 14, 16-17, 19, 21
y5  3 y