Download laboratory module

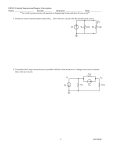
ENT 161 ELECTRIC CIRCUIT
ELECTRONIC BIOMEDICAL ENGINEERING
MECHATRONIC ENGINEERING SCHOOL
SEM 1, 2008/2009
EXPERIMENT 1
INTRODUCTION TO LAB INSTRUMENTS AND BASIC
MEASUREMENTS
1. OBJECTIVE:
1.1 To learn the operation of multimeter, function generator as a signal source,
operation of the oscilloscope as a measuring instrument
1.2 To learn the measurement techniques, which can be taken using the
oscilloscope.
2. INTRODUCTION
2.1 Bread Board (Socket Board)
The bread board has many strips of metal (copper usually) which run underneath the
board. The metal strips are laid out as shown below.
To use the bread board, the legs of components are placed in the holes (the sockets).
The holes are made so that they will hold the component in place. Each hole is
connected to one of the metal strips running underneath the board.
Each wire forms a node. A node is a point in a circuit where two components are
connected. Connections between different components are formed by putting their legs
in a common node. On the bread board, a node is the row of holes that are connected
by the strip of metal underneath.
The long top and bottom row of holes are usually used for power supply connections
and common/GND connection. The rest of the circuit is built by placing components and
connecting them together with jumper wires. Then when a path is formed by wires and
components from the positive supply node to the negative supply node, we can turn on
the power and current flows through the path and the circuit comes alive.
For chips with many legs (ICs), place them in the middle of the board so that half of the
legs are on one side of the middle line and half are on the other side.
-1-
ENT 161 ELECTRIC CIRCUIT
ELECTRONIC BIOMEDICAL ENGINEERING
MECHATRONIC ENGINEERING SCHOOL
SEM 1, 2008/2009
Example 1: How to transfer simple schematic diagram to bread board?
Figure 1.1 Breadboard Circuit.
-2-
ENT 161 ELECTRIC CIRCUIT
ELECTRONIC BIOMEDICAL ENGINEERING
MECHATRONIC ENGINEERING SCHOOL
SEM 1, 2008/2009
2.2 Multimeter.
2 PROBE WIRE
- RED - positive
- BLACK - common
READING
SCALE
DC VOLTAGE
MEASUREMENT
RANGE
CALIBRATION
KNOB
SELECTOR
KNOB
AC VOLTAGE
MEASUREMENT
RANGE
DC CURRENT
MEASUREMENT RANGE
RESISTANCE
MEASUREMENT RANGE
Figure 1.2 Analog Multimeter
2.2.1 DC Voltage Measurement Using Analog Multimeter.
1) Turn your "Selector Knob" to the suitable DC Voltage Measurement Range.
2) Drag your RED PROBE to the one of resistor lead and the BLACK PROBE to the
other resistor lead. See figure 1.3 for details.
3) Read the value of the voltage using selected range at Selector Knob.
2.2.2 DC Current Measurement Using Analog Multimeter.
1) Turn your "Selector Knob" to the suitable DC Current Measurement Range.
2) Brake the circuit at point where current need to be measured.
3) Drag your RED PROBE to the first point and the BLACK PROBE to the second
point. See figure 1.4 for details.
4) Read the value of the current using selected range at Selector Knob.
-3-
ENT 161 ELECTRIC CIRCUIT
ELECTRONIC BIOMEDICAL ENGINEERING
MECHATRONIC ENGINEERING SCHOOL
SEM 1, 2008/2009
Figure 1.3: Voltage Measurement
Figure 1.4: Current Measurement
2.2.3 Resistance Measurement Using Analog Multimeter.
1) Turn your "Selector Knob" to X1K Resistance Measurement Range.
-4-
ENT 161 ELECTRIC CIRCUIT
ELECTRONIC BIOMEDICAL ENGINEERING
MECHATRONIC ENGINEERING SCHOOL
SEM 1, 2008/2009
2) Touch your RED PROBE and BLACK PROBE together. You will see your meter
needle turn from ∞ to 0 Ω. Adjust your calibration knob until your meter needle
precisely on 0 Ω.
3) Drag your RED PROBE to the first lead of resistor the BLACK PROBE to the
second lead. See figure 1.3 for details.
4) Read the value of the resistor using selected range at Selector Knob. For example
If you select X1K at selector knob, the value from reading scale must be multiply
by 1000.
Figure 1.5: Resistance Measurement
-5-
ENT 161 ELECTRIC CIRCUIT
ELECTRONIC BIOMEDICAL ENGINEERING
MECHATRONIC ENGINEERING SCHOOL
SEM 1, 2008/2009
2.3 Familiarization with the oscilloscope
2.3.1 Introduction
The oscilloscope is an instrument of observation and measurement (Sometimes it is
called a scope for short). Its multiple applications stem from the fact that it can display
on its screen the Cartesian representation of various waveforms. This is accomplished
by displaying a variable signal on the vertical axis (Y) as a function of another variable
signal on horizontal axis (X). Some coommon examples are the amplitudes of voltages
(or currents) as a function of time (X).
2.3.2 Safety Precautions
You must understand the following safety precautions, and observe them during your
operation.
i)
ii)
iii)
Always plug the power cord of the scope into a properly wired receptacle
before connecting your probes or turning on the scope.
Do NOT intensify unnecessarily: the brightness of the spots or traces on the
viewing area must not be increased excessively. Excessively intensified spots
or traces may irritate an operator. They may also result in burning the
phosphorescence coating of the SRT in prolonged operation.
Do NOT apply an Excessively High Input Voltage: Each input connector has
rated maximum allowable input voltage.
2.3.3 Initializing the Oscilloscope

Basic Operation
Powering and Sweeping
i)
ii)
iii)
iv)
-6-
After confirming the line voltage, turn off the POWER switch, and connect the
power cord to the line receptacle.
Set the controls as below:
 MODE (vertical) CH1
 MODE (sweep) AUTO
 INTEN Mid-position
 POSITION (vertical) Mid-position
 POSITION (horizontal) Mid-position
Verify that CAL controls are locked in their detents (completely clockwise) and
are pushed in(X1 vertical magnification)
Switch on the oscilloscope and allow some time (about 30 sec) for it to warm
up. Then one can see a horizontal beam (CH 1 trace) appear on the screen. If
not, adjust the vertical (Y) position and horizontal (X) position knobs properly,
the beam will show up.
ENT 161 ELECTRIC CIRCUIT
ELECTRONIC BIOMEDICAL ENGINEERING
MECHATRONIC ENGINEERING SCHOOL
SEM 1, 2008/2009
Focusing
i)
ii)
iii)
iv)
v)

Set the trace to the center of the viewing area by the vertical POSITION
control.
Adjust horizontal (X) position and the horizontal gain to let the line occupy the
whole length of the screen but without surpassing it too much.
Set the TIME/DIV switch to 1 msec.
Set the brightness of the trace to desired degree by the INTRN control.
Adjust the FOCUS control to make the trace line thin and clear.
Vertical System Control
Selection of Signal Input Couplings:
Many kinds of signals can be measured such as dc, ac, and mixed signals. To
observe these signals correctly, an adequate signal input coupling must be selected
with the AC-GND-DC switch.
Selecting of Sensitivity
For accurate measurement of signal waveforms, it is essential to display adequate
amplitude of the waveforms on the viewing area. An excessively small or large
signal compared with the viewing area makes measurement difficult and inaccurate.
If the signal to be measured is small, it needs to be amplified; and if large, it needs to
be attenuated. The sensitivity is selected by the VOLTS/DIV switch and finely
adjusted by the VARIABLE (VAR) control. The sensitivity becomes equal to the
value indicated by the VOLTS/DIV switch when the VARIABLE control is set to the
fully clockwise position. The values show the voltage for one division on the viewing
area. The sensitivity is decreased when the VARIABLE control is turned left. When
the X10 MAG button is pushed, the sensitivity is magnified ten times of each
indicated values by the VOLTS/DIV switch.

Trigger Control
Triggering by signal supply: the following operation gives the most ordinary type
triggering (AUTO by internal triggering and AC coupling) and displays a 6-division
calibration voltage waveform on the viewing area.
1) Set the controls as below:
 COUPLING:AC
 AC-GND-DC: AC or DC
 SOURCE: CH1
2) Make sure the HOLDOFF control is rotated to MIN (completely counterclockwise)
-7-
ENT 161 ELECTRIC CIRCUIT
ELECTRONIC BIOMEDICAL ENGINEERING
MECHATRONIC ENGINEERING SCHOOL
SEM 1, 2008/2009
2.4 Familiarization with the Function Generator
Function generator is a device that acts like a source of signals. It can generate signals
such as sine, triangle, and square waveform, negative and positive pulses and dc levels
in continuous or gated form.
Figure 1.5 Function Generator
2.4.1 Function Generator Operation:
i)
ii)
iii)
iv)
v)
vi)
vii)
viii)
-8-
Connect the function generator with the scope according to the above figure.
Turn on the function generator and allow some time for it to warm up.
Adjust FREQUENCY DIAL to 1.0 and select FREQUENCY RANGE to 1k
Turn DC OFFSET, SYMMETRY to OFF (turn DUTY counterclockwise).
Select a sine waveform.
Connect Function OUTPUT/50 ohm CONEECTORE to the vertical input of
the scope.
Set the triggering system of the scope to correspond to the vertical input
channel, and adjust the triggering level to freeze the sine wave on the screen.
If you do not see a display, repeat and understand the steps given in section
A-4 from before.
Now use the function switch to obtain triangle wave and square wave, of the
same frequency.
ENT 161 ELECTRIC CIRCUIT
ELECTRONIC BIOMEDICAL ENGINEERING
MECHATRONIC ENGINEERING SCHOOL
SEM 1, 2008/2009
2.5 Measurement of Periodic Signal:
a. Apart from the observation of waveform of an input signal, one can measure its
amplitude because the Y-axis is calibrated in volts. One can also measure
various time parameter of the signal waveform because the X-axis is calibrated in
unit of time.
b. We first introduce the following parameters:
fg = frequency indicated by the notary scale of the generator.
fo = frequently obtained by measuring the period T with an oscilloscope.
c. Use the FREQUENCY DIAL, FREQUENCY RANGE to sweep through a broad
spectrum of frequency (from vary low to very high) of the signal, and observe the
waveforms on the screen.
d. Use the Function Generator to select other signals: sine, triangular and square
wave and repeat the previous step.
e. The frequency of the signal can be obtained by calculating the inverse of the
period, i.e. fo = 1 / To. Select the triangle wave and measure the period T o
corresponding to the frequency f o = 4kHz respectively. Note also the frequency f g
indicated on the rotary FREQUENCY DIAL.
f. The scope can measure the amplitude of any periodic signal waveforms
i)
Set up a sine wave of your choice at any frequency.
ii)
Adjust the signal amplitude to set the peak-to-peak value to 1V.
iii)
Repeat for a triangular waveform.
3. COMPONENTS AND EQUIPMENTS :
3.1 Breadboard – 1 unit
3.2 DC power supply – 1 unit
3.3 Digital Multimeter – 1 unit
3.4 Function Generator – 1 unit
3.5 Oscilloscope – 1 unit
3.6 Wires
3.7 Resistors:
3.7.1 500 Ω resistor - 1 pcs
3.7.2 2.2 kΩ resistor - 1 pcs
3.7.3 4.7 kΩ resistor - 1 pcs
3.7.4 10 µF capacitor - 1 pcs
-9-
ENT 161 ELECTRIC CIRCUIT
ELECTRONIC BIOMEDICAL ENGINEERING
MECHATRONIC ENGINEERING SCHOOL
SEM 1, 2008/2009
4. PROCEDURE:
4.1 PART (A).
4.1.1 Measure all your three resister given. Follow instruction from procedure 1.3
“Resistance Measurement Using Analog Multimeter”. Show your meter needle and
record your measurement in Table (A).1.
4.1.2 Base on Table (A).1 constructs the following circuit.
4.1.3 Set Vs for 10 V. Measure voltage drop for VR1, VR2, and VR3. Show your
meter needle and record your measurement in Table (A).2.
4.1.4 Measure current for IT, I1 and I2. Show your meter needle and record your
measurement in Table (A).3.
# Note: Make sure you range selection is suitable with your measurement.
4.2 PART (B).
Setting up the function generator.
4.2.1 Connect RED clip and BLACK clip to CH1 oscilloscope like figure 1.4.Set
Volt/Div at 0.5 V and Time/Div at 1ms.
4.2.2 Turn ON switch button and CAL on CAL position.
4.2.3 Set frequency range at range 1K and frequency type sine wave.
4.2.4 Turn AMP knob clockwise till you get 2 Vp-p displays at your oscilloscope
4.2.5 Turn FREQ knob clockwise till you get your frequency display at DISPLAY
PANEL 5.000 KHz. Draw your signal in Table (B).1: Sine wave.
-10-
ENT 161 ELECTRIC CIRCUIT
ELECTRONIC BIOMEDICAL ENGINEERING
MECHATRONIC ENGINEERING SCHOOL
SEM 1, 2008/2009
4.2.6 By using appropriate Volt/Div and Time/Div on oscilloscope set your Function
Generator to square wave at 500 Hz and 0.4 Vp-p. Draw your signal in Table (B).1:
square wave.
4.2.7 Construct following circuit. Set your Vs at 1Vp-p and 1KHz.Set your
oscilloscope at DUAL mode.
4.2.8 Connect your CH1 at point A and CH2 at point B. Adjust Volt/Div and Time/Div
to get the best view of your signal display. Measure CH2 (output) signal and draw
both signals in Table (B).2.
# Note that your CH1 at point A is your input voltage Vs.
4.2.9 Set gnd for both channels. Make sure both line is horizontally at 0 positions.
AC couple CH1 (input voltage). Adjust time/div until you get 25 small divisions per
half-cycle. (Note the # divisions ,K=25 = 180˚)
AC couple CH2 (output Voltage). Adjust CH2 Volt/Div so you get best view and
suitable reference. Count the # of small divisions between the 2 signals. This is your
phase shift,P. Calculate your phase different Ø using formula :
Ø = _P_ x 180
K
Draw both signals in Table (B).3.
-11-
ENT 161 ELECTRIC CIRCUIT
ELECTRONIC BIOMEDICAL ENGINEERING
MECHATRONIC ENGINEERING SCHOOL
SEM 1, 2008/2009
4.2.10 Set your Vs at 0.6 Vp-p/ 500 Hz. Repeat step 9 and 10.
-12-
ENT 161 ELECTRIC CIRCUIT
ELECTRONIC BIOMEDICAL ENGINEERING
MECHATRONIC ENGINEERING SCHOOL
SEM 1, 2008/2009
Name
:
______________________________
Matrix No
:
______________________________
Date : ______________
5. RESULT:
EXPERIMENT1: INTRO TO LAB INSTRUMENTS AND MEASUREMENTS.
Table
(A).1
Table
(A).2
Table
(A).3
Table
(B).1
Table
(B).2
Table
(B).3
MARKS
9
9
9
6
10
10
53
%
5.1 PART (A).
5.1.1 Table (A).1:
Range : ________
R1: 500 Ω
R1: _______ Ω.
Range : ________
R2: 2.2 KΩ
R2: _______ Ω.
Range : ________
R3: 47 KΩ
R3: _______ Ω.
5.1.2 Table (A).2:
Range : ________
VR1: _______ V.
-13-
Range : ________
VR2: _______ V.
Range : ________
VR3: _______ V.
ENT 161 ELECTRIC CIRCUIT
ELECTRONIC BIOMEDICAL ENGINEERING
MECHATRONIC ENGINEERING SCHOOL
SEM 1, 2008/2009
Name
:
______________________________
Matrix No
:
______________________________
Date : ______________
5.1.3 Table (A).3:
Range : ________
IT: _______ mA.
Range : ________
I1: _______ mA.
Range : ________
I2: _______ mA.
5.2 PART B.
5.2.1 Table (B).1
Time/Div: _________. (Sine wave)
Time/Div: _________. (Square wave)
5.2.2 Table (B).2
Time/Div: _______. Volt/Div: _______.
Vout: ________ Vp-p.
-14-
Time/Div: _______. Volt/Div: _______.
Vout: ________ Vp-p.
ENT 161 ELECTRIC CIRCUIT
ELECTRONIC BIOMEDICAL ENGINEERING
MECHATRONIC ENGINEERING SCHOOL
SEM 1, 2008/2009
Name
:
______________________________
Matrix No
:
______________________________
Date : ______________
5.2.3 Table (B).3
Time/Div: _______.
Phase different, Ø: __________.
Time/Div: _______.
Phase different, Ø: __________.
6. EXERCISE:
6.1 State the equipments that normally being used in electrical circuit analysis.
6.2 State the difference between analog and digital oscilloscope.
7. DISCUSSION:
The basic equipment for electrical circuit analysis is…
8. CONCLUSION:
The conclusion for this lab is…
-15-
ENT 161 ELECTRIC CIRCUIT
ELECTRONIC BIOMEDICAL ENGINEERING
MECHATRONIC ENGINEERING SCHOOL
SEM 1, 2008/2009
EXPERIMENT 2
KIRCHOFF’S LAW
1. OBJECTIVE:
1.1 Verify Kirchhoff’s current and voltage law.
1.2 Improve understanding on circuit analysis method.
2. INTRODUCTION:
From our consideration of series and parallel connections of resistor, we have observed
certain condition appertaining to each form of connection. For instance, in series circuit,
the sum of the voltage across each component is equal to the applied voltage, and for
parallel networks, the sum of the currents in the branches equal to the supply current.
Thus, that condition may state as below:
Kirchhoff’s current law. At any algebraic sum of the currents at the junction in the
network zero. Different signs are allocated to currents held to the flow towards the
junction and those away from it. For flow toward the sign is positive and negative for
current away from the branches.
Figure 2.1: Illustration Of Kirchhoff’s Current Law
From the figure 2.1 above the equation below describe the relationship between I1 , I2 ,
I3 I4 and I5 .
I1+I3=I2+I4=I5
(1)
Kirchhoff’s voltage law. At any instant in a closed loop, the algebraic sum of the emf ‘s
acting round the loop is equal to the algebraic sum of the pds round the loop.
-16-
ENT 161 ELECTRIC CIRCUIT
ELECTRONIC BIOMEDICAL ENGINEERING
MECHATRONIC ENGINEERING SCHOOL
SEM 1, 2008/2009
Figure 2.2: Illustration of Kirchhoff’s Voltage law.
As in figure 2.2, using Kirchhoff’s law voltage counter clockwise we ca write the the
equation as follow:
V1+V4=V2+V3
3. COMPONENTS AND EQUIPMENTS:
3.1 Breadboard – 1 unit
3.2 DC power supply – 1 unit
3.3 Digital Multimeter – 1 unit
3.4 Wires
3.5 Resistors:
3.5.1 1kΩ resistor - 2 pcs
3.5.2 2.2 kΩ resistor - 2 pcs
3.5.3 4.7 kΩ resistor - 1 pcs
-17-
(2)
ENT 161 ELECTRIC CIRCUIT
ELECTRONIC BIOMEDICAL ENGINEERING
MECHATRONIC ENGINEERING SCHOOL
SEM 1, 2008/2009
4. PROCEDURE:
4.1 Kirchhoff’s current law.
4.1.1 Consider the circuit in figure 2.3. Calculate theoretically current IT when V = 5
V. Record the value and verify the theoretically Kirchhoff’s current law between
node A and node B in pre-lab calculation.
Figure 2.3
4.2.2 4.1.2 Connect the circuit shown above figure 2.3 on the breadboard
4.2.3 Turn on DC power supply at 5V. By using the multimeter, measure the
current that flow through every resistor and record the value.
4.2.4 Prove Kirchhoff’s law practically.
4.2.5 Repeat step 3 and 4 by increasing the power supply to 10V and 15V
4.2.6 Record the value in table 2.1.
-18-
ENT 161 ELECTRIC CIRCUIT
ELECTRONIC BIOMEDICAL ENGINEERING
MECHATRONIC ENGINEERING SCHOOL
SEM 1, 2008/2009
4.2 Kirchhoff’s voltage law.
4.2.1 By referring the same circuit figure 2.3. Calculate theoretically voltage across
every resistor when V=5V. Record the calculation and verify theoretically Kirchhoff’s
voltage law for all closed loop below:
i. V,R1,R2,R5
ii. V,R1,R3,R5
iii. V,R1,R4,R5
4.2.2 Turn on DC power supply at 5V. By using multimeter, measure voltage drop
across every resistor. Record all measurement.
4.2.3 Prove Kirchhoff’s law practically.
4.2.4 Repeat step 2 for V=10V and V=15V
4.2.5 Record the value table 2.2.
-19-
ENT 161 ELECTRIC CIRCUIT
ELECTRONIC BIOMEDICAL ENGINEERING
MECHATRONIC ENGINEERING SCHOOL
SEM 1, 2008/2009
Name
:
______________________________
Matrix No
:
______________________________
Date : ______________
5. RESULT:
EXPERIMENT 2: KIRCHHOFF’S LAW
PRELAB
(A)
PRELAB
(B)
TABLE
1.1
TABLE
1.2
PROBLEM
(1)
PROBLEM
(2)
MARKS
5
5
16
16
6
6
54
6. PRE LAB CALCULATIONS.
V = 5 V.
6.1 Kirchhoff’s current law at node A.
6.2 Kirchhoff’s current law at node B.
-20-
%
ENT 161 ELECTRIC CIRCUIT
ELECTRONIC BIOMEDICAL ENGINEERING
MECHATRONIC ENGINEERING SCHOOL
SEM 1, 2008/2009
Name
:
______________________________
Matrix No
:
______________________________
Date : ______________
Table 2.1
DC Voltage Power Supply (V)
Current
V=5V
V=10V
V=15V
ITotal(mA)
IR1(mA)
IR2(mA)
IR3(mA)
IR4(mA)
Table 2.2
DC Voltage Power Supply (V)
Voltage
Drop
V=5V
Calculation
Experiment
VR1(V)
VR2(V)
VR3(V)
VR4(V)
VR5(V)
7. EXERCISE:
7.1 From figure below, what is value of VJ
-21-
V=10V
V=15V
ENT 161 ELECTRIC CIRCUIT
ELECTRONIC BIOMEDICAL ENGINEERING
MECHATRONIC ENGINEERING SCHOOL
SEM 1, 2008/2009
Name
:
______________________________
Matrix No
:
______________________________
Date : ______________
7.2 Determine the value of IJ if I1=0.47 A and I2=0.12A
VJ=________V
IJ=________A
7.3 Write down current relationship for junction a, b and c of the network shown in
figure below and determines the currents I3, I4 and I5.
7.4
Junction a;____________________________________________________
Junction b;____________________________________________________
Junction c;____________________________________________________
I3=_________A
-22-
I4=_________A
I5=_________ A
ENT 161 ELECTRIC CIRCUIT
ELECTRONIC BIOMEDICAL ENGINEERING
MECHATRONIC ENGINEERING SCHOOL
SEM 1, 2008/2009
Name
:
______________________________
Matrix No
:
______________________________
8. DISCUSSION:
The Kirchoff’s current and voltage laws …
9. CONCLUSION:
The conclusion for this lab is…
-23-
Date : ______________
ENT 161 ELECTRIC CIRCUIT
ELECTRONIC BIOMEDICAL ENGINEERING
MECHATRONIC ENGINEERING SCHOOL
SEM 1, 2008/2009
EXPERIMENT 3
Parallel Circuits & Voltage Divider Rules for Series Circuit
1.
OBJECTIVE:
1.1 To investigate the characteristics of a parallel circuit.
1.2 To examine the relationship between combinations of voltage drops and combinations
of resistance values in a series circuit using voltage divider rules.
2.
INTRODUCTION:
2.1 Parallel Circuits:
A Parallel circuit has certain characteristics and basic rules summarized here:
 A parallel circuit has two or more paths for current to flow through.
 Voltage is the same across each component of the parallel circuit.
 The sum of the currents through each path is equal to the total current that flows
from the source.
 You can find total resistance in a Parallel circuit with the following formula:
1/Rt = 1/R1 + 1/R2 + 1/R3 +...
Rt = R (total)
 If one of the parallel paths is broken, current will continue to flow in other paths.
2.1.1
A parallel circuit has two or more paths for current to flow through.
This is self explanatory. Simply remember that PARALLEL means two paths up
to thousands of paths. The flow of electricity is divided between each according
to the resistance along each route.
Figure 3.1
2.1.2
Rule 1 for parallel circuit.
Voltage is the same across each component of the parallel circuit.
You may remember from the last section that the voltage drops across a
resistor in series. Not so with a parallel circuit. The voltage will be the same
-24-
ENT 161 ELECTRIC CIRCUIT
ELECTRONIC BIOMEDICAL ENGINEERING
MECHATRONIC ENGINEERING SCHOOL
SEM 1, 2008/2009
anywhere in the circuit.
Figure 3.2
2.1.3
Rule 2 for parallel circuit.
The sum of the currents through each path is equal to the total current
that flows from the source.
If one path is drawing 1 amp and the other is drawing 1 amp then the total is 2
amps at the source. If there are 4 branches in this same 2 amp circuit, then one
path may draw 1/4A (.25A), the next 1/4A (.25), the next 1/2A (.5A) and the last
1A. Don't worry, the next rule will show you how to figure this out. Simply
remember for now that the branch currents must tally to equal the source
current.
Figure 3.3
Rule 3 for parallel circuit.
2.2 Voltage Divider
The voltage across one resistor equals the ratio of that resistor's value and the sum of
resistances times the voltage across the series combination. This concept is so
pervasive it has a name: voltage divider.
-25-
ENT 161 ELECTRIC CIRCUIT
ELECTRONIC BIOMEDICAL ENGINEERING
MECHATRONIC ENGINEERING SCHOOL
SEM 1, 2008/2009
Referring to Single Loop circuit in Figure 3.4, which yields
Vin = Vout1 + Vout2,
where, Vout1 = R1i
Vout2 = R2i
Combining these equations, we find
And
Vin = R1i + R2i
i =
Figure 3.4
V / ( R1 + R2 ).
Single loop circuit
So finally the equations for voltage divider for both resistors are,
3.
Vout1 =
R1
Vin
R1 + R2
Vout2 =
R2
Vin
R1 + R2
COMPONENT AND EQUIPMENT:
3.1 Breadboard – 1 unit
3.2 DC power supply – 1 unit
3.3 Digital Multimeter – 1 unit
3.4 Wires
3.5 Resistors:
3.5.1 1.2 kΩ resistor - 1 pcs
-26-
ENT 161 ELECTRIC CIRCUIT
ELECTRONIC BIOMEDICAL ENGINEERING
MECHATRONIC ENGINEERING SCHOOL
SEM 1, 2008/2009
3.5.2
3.5.3
3.5.4
3.5.5
3.5.6
4.
1.8 kΩ resistor - 1 pcs
2.2 kΩ resistor - 1 pcs
3.3 kΩ resistor - 2 pcs
5.6 kΩ resistor - 1 pcs
33 kΩ resistor - 1 pcs
PROCEDURE:
4.1 Parallel Circuit:
4.1.1
Part 1(a) - Voltage characteristic in a parallel circuit.
a)
Connect the circuit in Figure 3.5. Adjust the voltage source to a value of
12 volts (with the circuit connected).
b)
Using the DMM, measure the voltage across each resistor. Record your
measurements in Table 5.1
Figure 3.5
4.1.2
Schematic diagram of circuits.
Part 1(b) - Current relationships in a parallel circuit.
a)
Connect the circuit in Figure 3.6. Make sure that the source voltage is
properly set to 12 volts with the circuit connected.
b)
Using a current meter, measure the current through each resistor and the
total current. Record your measurement in Table 5.1.
-27-
ENT 161 ELECTRIC CIRCUIT
ELECTRONIC BIOMEDICAL ENGINEERING
MECHATRONIC ENGINEERING SCHOOL
SEM 1, 2008/2009
Figure 3.6
4.1.3
Schematic diagram of circuits.
Part 1(c) - Resistance relationship in a parallel circuit.
a)
Connect the circuit in Figure 3.7. Note that there is no source voltage
connected.
b)
Using a DMM, measure the total resistance. Record your measurement in
Table 3.1.
Figure 3.7
c)
Schematic diagram of circuits.
Remove each resistor from the circuit. Using the DMM, individually
measure R1, R2, and R3. Record your measurement.
4.2 Voltage Divider for Series Circuit.
4.2.1 Connect the circuit in Figure 3.8.
4.2.2
Measure and record below the voltage drop across each resistor. When
measuring VAB, the voltmeter probe should be connected to point A and the
common lead to point B. This would be expressed as VAB. Note that in the
subscript “AB”, the first letter “A” is the point to which the probe is connected
-28-
ENT 161 ELECTRIC CIRCUIT
ELECTRONIC BIOMEDICAL ENGINEERING
MECHATRONIC ENGINEERING SCHOOL
SEM 1, 2008/2009
and the second letter “B” is the point to which the common lead is connected.
Therefore, the expression VAB means the voltage at point “A” in respect to point
“B”.
4.2.3
Properly label these measured voltage drops on each resistor in Figure 3.9.
Mark the polarity (use a + and a - to indicate polarity) of the voltage drop on
each resistor.
4.2.4
Measure the voltage, VCE, between point C and point E. When measuring, the
voltmeter probe should be connected to point C and the common lead to point
E. This would be expressed as VCE. Note that in the subscript “CE”, the first
letter “C” is the point to which the probe is connected and the second letter “E”
is the point to which the common lead is connected. Therefore, the expression
VCE means the voltage at point “C” in respect to point “E”. Record this voltage in
Table 3.2.
4.2.5
In a like manner, measure and record the following in Table 3.2.
VAC =
VDG =
VCA =
VEA =
Figure 3.9
-29-
(note opposite polarity!)
VBF =
Schematic diagram of circuits.
VCG = _______
ENT 161 ELECTRIC CIRCUIT
ELECTRONIC BIOMEDICAL ENGINEERING
MECHATRONIC ENGINEERING SCHOOL
SEM 1, 2008/2009
Name
:
______________________________
Matrix No
:
______________________________
5.
Date: ______________
RESULT:
EXPERIMENT 3: Parallel Circuits & Voltage Divider Rules for Series Circuit.
5.1 Information:
5.1.1
Always use the measured value of resistance for all calculations.
5.1.2
Always adjust the power supply voltage with the circuit connected.
5.1.3
When measuring voltage, the voltmeter must be connected across the circuit
element of interest.
5.1.4
When measuring current, the current meter must be inserted into the “break”
in the circuit (in series).
TABLE 3.1
15
TABLE 3.2
PROBLEM
(1)
PROBLEM
(2)
MARKS
10
10
50
15
%
Table 5.1 Voltage, current and resistance measured in Part 1
Part 1 (A)
Voltage (V)
Part 1 (B)
Current (mA)
Part 1 (C)
Resistance (ohm)
VR1 =
IR1 =
Rtotal =
VR2 =
IR2 =
R1 =
VR3 =
IR3 =
R2 =
Itotal =
R3 =
-30-
ENT 161 ELECTRIC CIRCUIT
ELECTRONIC BIOMEDICAL ENGINEERING
MECHATRONIC ENGINEERING SCHOOL
SEM 1, 2008/2009
Name
:
______________________________
Matrix No
:
______________________________
Date: ______________
Table 3.2 Voltage measured in Part 2
Part 2
VR1 = VAB
VR2 = VBC
VR3 = VCD
VR4 = VDE
VR5 = VEF
VR6 = VFG
VCE
VCA
VAC
VDG
VEA
VBF
VCG
-31-
Voltage Measured (V)
ENT 161 ELECTRIC CIRCUIT
ELECTRONIC BIOMEDICAL ENGINEERING
MECHATRONIC ENGINEERING SCHOOL
SEM 1, 2008/2009
Name
:
______________________________
Matrix No
:
______________________________
Date: ______________
6. EXERCISE:
6.1 Find the equivalent resistance seen by the source and current i.
-32-
ENT 161 ELECTRIC CIRCUIT
ELECTRONIC BIOMEDICAL ENGINEERING
MECHATRONIC ENGINEERING SCHOOL
SEM 1, 2008/2009
Name
:
______________________________
Matrix No
:
______________________________
Date: ______________
6.2 In the voltage divider shown the power delivered by the source is 9mW and Vi = V/4.
Find R, V, Vi and i.
-33-
ENT 161 ELECTRIC CIRCUIT
ELECTRONIC BIOMEDICAL ENGINEERING
MECHATRONIC ENGINEERING SCHOOL
SEM 1, 2008/2009
Name
:
______________________________
Matrix No
:
______________________________
7. DISCUSSION:
The current and voltage values is ..
8. CONCLUSION:
The conclusion for this lab is…
-34-
Date: ______________
ENT 161 ELECTRIC CIRCUIT
ELECTRONIC BIOMEDICAL ENGINEERING
MECHATRONIC ENGINEERING SCHOOL
SEM 1, 2008/2009
EXPERIMENT 4
Thevenin’s And Norton’s Theorem
1.
OBJECTIVE:
1.3 To compare between analyze of complex circuit and Thevenin /Norton equivalent
circuit.
1.2 To learn concept of ideal current source.
2.
INTRODUCTION:
The Thevenin equivalent method allows you to replace any circuit consisting of
independent sources, dependent sources and resistors with simple circuit consisting of a
single voltage sources in series with a single resistor where the simple circuit is equivalent
to the original circuit. This means that a resistor first attached to the original circuit and
then attached to the simple circuit could not distinguish between the two circuits, since the
resistor would experience the same voltage drop, the same current flow and thus the
same power dissipation.
The Thevenin equivalent method can thus be used to reduce the complexity of a
circuit and make it much easier to analyze. A Norton equivalent circuit consists of a single
current source in parallel with a single resistor and can be constructed from a Thevenin
equivalent circuit using source transformation. Thus in this section we will present a
technique for calculating the component values for a Thevenin equivalent circuit, if you
want the Norton equivalent circuit, you can calculate the Thevenin equivalent circuit and
use source transformation.
There are three important quantities that make up a Thevenin equivalent circuit,
the open-circuit voltage, Voc, the short circuit current, isc and the Thevenin equivalent
resistance, RTh. In the Thevenin equivalent circuit, the value of the voltage source is Voc
and the value of the series resistor is RTh. In the Norton equivalent, the value of the current
source is isc and the value of the parallel resistor is RTh but it is not necessary to calculate
all three quantities, since they are related by following equation:
Voc=RThisc
(1)
Thus we need to determine just two of these three quantities and can use their relationship
to find the third quantity, if desired. In circuit containing only independent sources and
resistor, our Thevenin equivalent method will determine the values of voc and RTh. When a
circuit also contains dependent sources we will modify the method and determine voc and
RTh.
-35-
ENT 161 ELECTRIC CIRCUIT
ELECTRONIC BIOMEDICAL ENGINEERING
MECHATRONIC ENGINEERING SCHOOL
SEM 1, 2008/2009
3.
COMPONENT AND EQUIPMENT:
3.1 Breadboard – 1 unit
3.2 DC power supply – 1 unit
3.3 Digital Multimeter – 1 unit
3.4 Wires
3.5 Resistors:
3.5.1 100 Ω resistor - 1 pcs
3.5.2 470 Ω resistor - 1 pcs
3.5.3 1.0 kΩ resistor - 1 pcs
3.5.4 1.5 kΩ resistor - 1 pcs
3.5.5 4.7 kΩ resistor - 1 pcs
3.5.6 33 kΩ resistor - 1 pcs
4.
PROCEDURE:
4.1 Thevenin’s Theorem:
4.1.1
Consider the circuit in Figure 4.1 .Find its Thevenin’s equivalent circuit. Draw
and label your circuit in Figure 4.4.
4.1.2
Build the circuit shown in Figure 4.1 on the breadboard mounted to the bench
top, using the DC power supply as vs. Once you have built the circuit, set the
value of vs to 10 V. Be sure to use the multimeter to make sure the terminal
voltage produced by the power supply is as close to 10 V as you can get it.
Figure 4.1
4.1.3
4.1.4
4.1.5
Schematic diagram of circuits.
Measure and record the voltage across a-b terminal. This is Thevenin
equivalent circuit voltage, voc.
Remove DC power supply from the circuit and disconnect its terminal. Measure
resistance across a-b terminal. Record its value as this is Thevenin equivalent
resistance, RTh.
Calculate the voltage drop across RL using this formula below:
VRL= vocRL
(2)
RTh +Rl
-36-
ENT 161 ELECTRIC CIRCUIT
ELECTRONIC BIOMEDICAL ENGINEERING
MECHATRONIC ENGINEERING SCHOOL
SEM 1, 2008/2009
4.1.6
Connect RL and DC power supply back to the circuit. Turn on the power
supply, measure and record the voltage across RL (a-b terminal).
4.1.7
Repeat step 1 till 6 for circuit in Figure 4.2.
Figure 4.2
Schematic diagram of circuits.
4.2 Norton’s Theorem
4.2.1
Consider the circuit in Figure 4.1. Find its Norton’s equivalent circuit. Draw and
label your circuit in Figure 4.4.
4.2.2
Connect the circuit in Figure 4.1. Replace RL with ammeter (multimeter) and
make sure the polarity of ammeter is right. Turn on DC power supply and
record the current. This is the value of Norton equivalent circuit current source,
isc.
4.2.3
Calculate voltage drop across RL from equivalent circuit using formula below:
VRL=iscRThRL
(3)
RTh+RL
4.2.4
Connect RL to the circuit and remove ammeter. Turn on power supply,
measure and record the voltage drop across RL (a-b terminal). Compare
calculated VRL with measured one.
4.2.5
-37-
Repeat step 2 to 4 for circuit in Figure 4.2.
ENT 161 ELECTRIC CIRCUIT
ELECTRONIC BIOMEDICAL ENGINEERING
MECHATRONIC ENGINEERING SCHOOL
SEM 1, 2008/2009
Name
:
______________________________ Date : ______________
Matrix No
:
______________________________
5.
RESULT:
EXPERIMENT 4: Thevenin’s and Norton’s Theorem
Figure
4.5
Table
4.1
Table
4.2
Figure
4.2
Table
4.3
Table
4.4
Problem
1
Problem
2
MARKS
4
8
8
4
6
6
6
6
48
5.1 Thevenin’s Theorem
For circuit in Figure 4.1
Figure 4.5 : Thevenin equivalent circuit for circuit in Figure 4.1
-38-
%
ENT 161 ELECTRIC CIRCUIT
ELECTRONIC BIOMEDICAL ENGINEERING
MECHATRONIC ENGINEERING SCHOOL
SEM 1, 2008/2009
Name
:
______________________________ Date : ______________
Matrix No
:
______________________________
Table 4.1:
Measured and Calculated Value for circuit in Figure 4.1
Parameter
Measured Value
Calculated Value
Voc
RTh
VRL
For circuit in Figure 4.2
Table 4.2:
Parameter
Voc
RTh
VRL
-39-
Measured and Calculated Value for circuit in Figure 4.2
Measured Value
Calculated Value
ENT 161 ELECTRIC CIRCUIT
ELECTRONIC BIOMEDICAL ENGINEERING
MECHATRONIC ENGINEERING SCHOOL
SEM 1, 2008/2009
Name
:
______________________________ Date : ______________
Matrix No
:
______________________________
5.2 Norton’s Theorem
For circuit in Figure 4.1
Figure 4.2:
Table 4.3:
Parameter
iSC
VRL
-40-
Norton equivalent circuit for circuit in Figure 4.1
Measured and Calculated Value for circuit in Figure 4.1
Measured Value
Calculated Value
ENT 161 ELECTRIC CIRCUIT
ELECTRONIC BIOMEDICAL ENGINEERING
MECHATRONIC ENGINEERING SCHOOL
SEM 1, 2008/2009
Name
:
______________________________ Date : ______________
Matrix No
:
______________________________
For circuit in figure 4.2
Table 4.4:
Parameter
iSC
VRL
-41-
Measured and Calculated Value for circuit in Figure 4.2
Measured Value
Calculated Value
ENT 161 ELECTRIC CIRCUIT
ELECTRONIC BIOMEDICAL ENGINEERING
MECHATRONIC ENGINEERING SCHOOL
SEM 1, 2008/2009
Name
:
______________________________ Date : ______________
Matrix No
:
______________________________
6. EXERCISE:
6.1 Determine the value of Rth, Voc at a-b terminal and i for circuit in Figure 4.6.
Figure 4.6
-42-
ENT 161 ELECTRIC CIRCUIT
ELECTRONIC BIOMEDICAL ENGINEERING
MECHATRONIC ENGINEERING SCHOOL
SEM 1, 2008/2009
Name
:
______________________________ Date : ______________
Matrix No
:
______________________________
6.2 The Thevenin equivalent resistance RTH for the network in figure 4.7 was 3.2 kΩ. Detail
how this could be altered to 2 kΩ by using a single resistor placed across terminal A and
B. Calculate the value of the resistor that will accomplish this. Will the Thevenin voltage
change?
Figure 4.7
Value of resistor:________________Ω
-43-
ENT 161 ELECTRIC CIRCUIT
ELECTRONIC BIOMEDICAL ENGINEERING
MECHATRONIC ENGINEERING SCHOOL
SEM 1, 2008/2009
Name
:
______________________________
Matrix No
:
______________________________
7. DISCUSSION:
The Thevenin and Norton Theorem is…
8. CONCLUSION:
The conclusion for this lab is…
-44-
Date: ______________
ENT 161 ELECTRIC CIRCUIT
ELECTRONIC BIOMEDICAL ENGINEERING
MECHATRONIC ENGINEERING SCHOOL
SEM 1, 2008/2009
EXPERIMENT 5
Maximum Power Transfer Theorem
1.
OBJECTIVE
1.1 To verify by measurement, that maximum power is developed in a load when the load
resistance is equal to the internal resistance of the source.
1.2 To construct a graph, using measured values of voltage, current and load resistance
and calculated power to verify graphically Objective 1 above.
2.
INTRODUCTION
The maximum power transfer theorem states that when the load resistance is equal to the
source's internal resistance, maximum power will be developed in the load. Since most low
voltage DC power supplies have a very low internal resistance (10 ohms or less) great difficulty
would result in trying to effect this condition under actual laboratory experimentation. If one were
to connect a low value resistor across the terminals of a 10 volt supply, high power ratings
would be required, and the resulting current would probably cause the supply's current rating to
be exceeded. In this experiment, therefore, the student will simulate a higher internal resistance
by purposely connecting a high value of resistance in series with the DC voltage supply's
terminal. Refer to Figure 5.1 below. The terminals (a & b) will be considered as the power
supply's output voltage terminals. The student will use a potentiometer as a variable size of load
resistance. For various settings of the potentiometer representing RL, the load current and load
voltage will be measured. The power dissipated by the load resistor can then be calculated. For
the condition of RL = Ri, the student will verify by measurement that maximum power is
developed in the load resistor.
3.
COMPONENTS AND EQUIPMENTS
3.1 Breadboard – 1 Unit
3.2 DC Power Supply – 1 Unit
3.3 Digital Multimeter – 1 Unit
3.4 Potentiometer:
-45-
3.4.1
1– 1kΩ - 1pcs
3.4.2
1– 10kΩ - 1pcs
ENT 161 ELECTRIC CIRCUIT
ELECTRONIC BIOMEDICAL ENGINEERING
MECHATRONIC ENGINEERING SCHOOL
SEM 1, 2008/2009
4.
PROCEDURE
4.1 Refer to Figure 5.2.
4.1.1 Using the DMM set the potentiometer to 100 ohms.
4.1.2 Connect the circuit of Figure 1. Measure the current through and the
voltage across RL. Record this data in Table 5.1.
4.1.3 Remove the potentiometer and set it to 200 ohms. Return it to the circuit
and again measure the current through and the voltage across RL.
Record.
4.1.4 Continue increasing the potentiometer resistance in 100 ohm steps until
the value 1 k ohms is reached, each time measuring the current and
voltage and recording same in Table 5.1. Be sure the applied voltage
remains at the fixed value of 10 volts.
4.1.5 C hange to the 10 kohm potentiometer. Continue measuring and
recording the current through and the voltage across RL. Increase the
potentiometer value in 1 kohms increments till 10 kohms is reached.
4.2 For each value of RL in Table 5.1, calculate the power input to the circuit using
the formula:
Pinput = Einput x IL = 10 x IL, since Ein is always a constant 10 volts.
4.3 For each value of RL in Table 1, calculate the power output (the power
developed in RL) using the formula: Pout = ERL x IL.
-46-
ENT 161 ELECTRIC CIRCUIT
ELECTRONIC BIOMEDICAL ENGINEERING
MECHATRONIC ENGINEERING SCHOOL
SEM 1, 2008/2009
4.4 For each value of RL in Table 1, calculate the circuit efficiency using the
formula: % efficiency = Pout/Pin x 100.
4.5 On linear graph 5.1, plot the curve of power output vs. RL. Plot RL on the
horizontal axis (independent variable). Plot power developed in RL on the
vertical axis (dependent variable). Label the point on the curve representing the
maximum power.
-47-
ENT 161 ELECTRIC CIRCUIT
ELECTRONIC BIOMEDICAL ENGINEERING
MECHATRONIC ENGINEERING SCHOOL
SEM 1, 2008/2009
Name
:
______________________________
Matrix No
:
______________________________
5.
Date: ______________
RESULT
Table 5.1
RL (Ω)
100
200
300
400
500
600
700
800
900
1,000
2,000
3,000
4,000
5,000
6,000
7,000
8,000
9,000
10,000
-48-
IL (mA)
ERL (V)
Pinput (mW)
Poutput (mW)
% eff.
ENT 161 ELECTRIC CIRCUIT
ELECTRONIC BIOMEDICAL ENGINEERING
MECHATRONIC ENGINEERING SCHOOL
SEM 1, 2008/2009
Name
:
______________________________
Matrix No
:
______________________________
Graph 5.1
Power Output vs. RL
-49-
Date: ______________
ENT 161 ELECTRIC CIRCUIT
ELECTRONIC BIOMEDICAL ENGINEERING
MECHATRONIC ENGINEERING SCHOOL
SEM 1, 2008/2009
Name
:
______________________________
Matrix No
:
______________________________
6.
Date: ______________
EXERCISE
6.1 What is the relationship of RL and Ri, at the point where the load dissipates maximum
power
6.2 Find RL for maximum power transfer and the maximum power that can be transferred
in the network below.
-50-
ENT 161 ELECTRIC CIRCUIT
ELECTRONIC BIOMEDICAL ENGINEERING
MECHATRONIC ENGINEERING SCHOOL
SEM 1, 2008/2009
Name
:
______________________________
Matrix No
:
______________________________
Date: ______________
7. DISCUSSION:
The maximum power transfer theorem is…
8. CONCLUSION
Based on measurement data and graph, make your overall conclusion by referring to the
objective of this experiment.
-51-
ENT 161 ELECTRIC CIRCUIT
ELECTRONIC BIOMEDICAL ENGINEERING
MECHATRONIC ENGINEERING SCHOOL
SEM 1, 2008/2009
EXPERIMENT 6 (A)
Capacitor
1.
OBJECTIVE
1.1 Compare total capacitance, charge, and voltage drop for capacitors connected in
series and in parallel.
1.2 Test capacitors with an ohmmeter and a voltmeter as a basic charging test.
2.
INTRODUCTION
A capacitor is formed whenever two conductors are separated by an insulting material. When a
voltage exists between the conductors, there will be an electric charge between the conductors.
The ability to store an electric charge is a fundamental property of capacitors and affects both
dc and ac circuits. Capacitors are made with large flat conductors called plates. The plates are
separated with an insulating material called a dielectric. The ability to store charge increases
with larger plate size and closer separation. When a voltage is connected across a capacitor,
charge will flow in the external circuit until the voltage across the capacitor is equal to the
applied voltage. The charge that flows is proportional to the size of the capacitor and the applied
voltage. This is a fundamental concept for capacitors and is given by the equation:
Q = CV
(1)
Where Q is the charge in coulombs, C is the capacitance in farads and V is the applied voltage.
An analogous situation is that of putting compressed air into a bottle. The quantity of air is
directly proportional to the capacity of the bottle and the applied pressure. Recall that current is
defined as charge per time; that is:
Q
I = ---(2)
t
where I is the current in amperes, Q is the charge in coulombs, and t is the time in seconds.
This equation can be rearranged as
Q = It
(3)
If we connect two capacitors in series with a voltage source,the same charging current flows
through both capacitors. Since this current flow for the same amount of time, it can be seen that
the total charge, QT, must be the same as the charge on each capacitor; that is:
QT = Q1 + Q2
(4)
Charging capacitors in series causes the same charge to be across each capacitor; however
the total capacitance decreases. In a series circuit, the total capacitance is given by the formula:
-52-
ENT 161 ELECTRIC CIRCUIT
ELECTRONIC BIOMEDICAL ENGINEERING
MECHATRONIC ENGINEERING SCHOOL
SEM 1, 2008/2009
(5)
Now consider capacitors in parallel. In parallel circuit, the total current is equal to the sum of the
currents in each branch as stated by Kirchhoff’s current law. If this current flows for the same
amount of time, the total charge leaving the voltage source will equal the sum of the charges
which flow in each branch. Mathematically,
QT = Q1 + Q2 + … + Q k
(6)
Capacitors connected in parallel will raise the total capacitance because more charge can be
stored at a given voltage. The equation for the total capacitance of parallel capacitors is:
CT = C1 + C2 + … + Ck
(7)
There are quick test that can verify that a capacitor, larger than about 0.01 µF, can be charged.
Although these tests are not comprehensive, they are useful in troubleshooting a faulty
capacitor. A voltmeter can be used to check a capacitor with voltage applied. The voltmeter is
connected in series with the capacitor and a dc voltage as indicated in Figure 6.1. When
voltage is first applied, the capacitor charges through the voltmeter’s large series resistance. As
it charges, voltage will appear across it, and the voltmeter indication will soon show a very small
voltage. Large electrolytic capacitors may have leakage current that makes them appear bad,
especially with a very high impedance voltmeter. In this case, use the test as a relative test,
comparing the reading with a similar capacitor which you know is good.
The simple charging tests are satisfactory for determining if a gross failure has occurred. They
do not indicate the value of the capacitor or if its value has changed. Value change is a common
fault in capacitors, and there are other failures, such as high leakage current and dielectric
absorption (the result of internal dipoles remaining in a polarized state even after the capacitor
discharges). Some low cost DMMs include built-in capacitance meters. A more comprehensive
test can be provided by an instrument such as s dynamic component analyzer, which measures
the value as well as leakage current and dielectric absorption.
-53-
ENT 161 ELECTRIC CIRCUIT
ELECTRONIC BIOMEDICAL ENGINEERING
MECHATRONIC ENGINEERING SCHOOL
SEM 1, 2008/2009
3.
COMPONENTS AND EQUIPMENTS
3.1 Breadboard
3.2 DC Power Supply
3.3 Digital Multimeter
3.4 LED – 2pcs
3.5 Resistor 1kΩ - 1pcs
3.6 Capacitor (35V or Greater)
3.6.1 100µF
3.6.2 4.7µF
3.6.3 1.0µF
3.6.4 0.1µF
3.6.5 0.01µF
4.
PROCEDURE
4.1 Obtain 5 capacitors as listed in Table 6.1. Check each capacitor using the ohmmeter
test described in the introduction. Record the results of the test on Table 6.1.
4.2 Test each capacitor using the voltmeter test. Because of slow charging, a large
electrolytic capacitor may appear to fail this test. Check the voltage rating on the
capacitor to be sure it is not exceeded. The working voltage is the maximum voltage
that can safely be applied to the capacitor. Record your results in Table 6.1.
4.3 Connect the circuit shown in Figure 6.2. The switches can be made from wire. Leave
both switches open. The light-emitting diodes (LEDs) and the capacitor are both
polarized components, they must be connected in the correct direction in order to work
properly.
-54-
ENT 161 ELECTRIC CIRCUIT
ELECTRONIC BIOMEDICAL ENGINEERING
MECHATRONIC ENGINEERING SCHOOL
SEM 1, 2008/2009
Figure 6.2
4.4 Close S1 and observe the LED1 and LED2. Then open S1 and then close S2. Describe
your observations in Table 6.2.
4.5 Now connect C2 in series with C1. Open both switches. Make certain the capacitors
are fully discharged by shorting them with a piece of wire; then close S 1. Measure the
voltage across each capacitor. Do this quickly to prevent the meter from causing the
capacitors to discharge. Record the voltages in Table 6.2.
4.6 Using the measured voltages, compute the charge on each capacitor. Then open S1
and close S2. Record the computed charge and your observations in Table 6.2.
4.7 Change the capacitors from series to parallel. Open both switches. Ensure the
capacitors are fully discharged. Then close S1. Quickly measure the voltage across
the parallel capacitors and enter the measured voltage in Table 6.2.
4.8 Using the measured voltage across the parallel capacitors, compute the charge on
each one. Then open S1 and close S2. record the computed charge and your
observations in Table 6.2.
4.9 Replace the +12 V dc source with a signal generator. Set the signal generator to a
square wave and set the amplitude to 12 Vpp. Set the frequency to 10 Hz. Close both
switches. Notice the difference in the LED pulses. This demonstrates one of the
principal applications of large capacitors that of filtering. Record your observations.
-55-
ENT 161 ELECTRIC CIRCUIT
ELECTRONIC BIOMEDICAL ENGINEERING
MECHATRONIC ENGINEERING SCHOOL
SEM 1, 2008/2009
EXPERIMENT 6 (B)
RC Circuit
1.
OBJECTIVE
1.1 To explores the exponential time dependence of a RC Circuit
1.2 The characteristic of RC circuit.
2.
INTRODUCTION
A capacitor is a device for storing charge. The ability of a capacitor to hold a charge is
measured by its capacitance C. For a capacitor, Q = CV, where Q is the charge on one of the
capacitor plates, C is the capacitance of the capacitor, and V is the potential difference
maintained across the capacitor plates. The unit of capacitance is the Farad (F), where one
Farad equals one Coulomb per volt (1F = 1C/V).
If a capacitor is connected to a battery, it will cause a charge +Q to develop on one plate and a
charge -Q to develop on the other. If the battery is removed from the circuit the capacitor is
connected to a resistor, then the capacitor will discharge through the resistor. The voltage
across the resistor is given by V = IR, where I is the current through the resistor at a given time,
and R is the resistance of the resistor. Since V = Q/C, = we can also write
I = V/R = Q/RC
As the capacitor discharges, Q becomes smaller, and I also becomes smaller.The current at
any time t is given by :
I = I0e-t/RC = I0e-t/τ
where I0 = initial value of the current, ti = time elapsed in seconds since the discharging began,
τ = RC = capacitive time constant for the RC circuit, and e = 2.71828... .
A plot of I versus t is shown on the left below. This plot is an exponential decay curve. The
current in the RC circuit exponentially decays over time. If we plot the natural logarithm (ln) of
the ratio I/I0, the graph (seen on the right below) becomes a straight line whose slope is -1/τ.
-56-
ENT 161 ELECTRIC CIRCUIT
ELECTRONIC BIOMEDICAL ENGINEERING
MECHATRONIC ENGINEERING SCHOOL
SEM 1, 2008/2009
3.
COMPONENTS AND EQUIPMENTS
3.1 Breadboard
3.2 DC Power Supply
3.3 Digital Multimeter
3.4 Resistor 100kΩ - 1pcs
3.5 Capacitor 100µF – 2pcs
4.
PROCEDURE
4.1 Connect your DC power supply, capacitor, resistor and voltmeter all in parallel as in
Figure 6.2.
Figure 6.2.
4.2 Let switch at point 2.
4.3 Adjust your power supply for a voltage of 5.00 V.
4.4 Simultaneously change the switch to point 1 and start your stopwatch.
-57-
ENT 161 ELECTRIC CIRCUIT
ELECTRONIC BIOMEDICAL ENGINEERING
MECHATRONIC ENGINEERING SCHOOL
SEM 1, 2008/2009
4.5 Take data every 10 seconds for at least three time constants. Record your data in
Table 6.3.
4.6 Plot Voltage vs. time
4.7 Plot ln(V/V0) vs. time. Determine the time constant and capacitance value from the
slope of this plot and a measured value of resistance.
-58-
ENT 161 ELECTRIC CIRCUIT
ELECTRONIC BIOMEDICAL ENGINEERING
MECHATRONIC ENGINEERING SCHOOL
SEM 1, 2008/2009
Name
:
______________________________
Matrix No
:
______________________________
5.
Date : ______________
RESULT
Table
6.1
Table
6.2
(5)
(12)
Questions Table5.3
(5)
(14)
Graph
6.1
Graph
6.2
MARKS
(5)
(5)
(46)
%
Table 6.1
Capacitor
Listed
C1
C2
C3
C4
C5
100 µF
4.7 µF
1.0 µF
0.1 µF
0.01 µF
Voltmeter test (Pass / Fail)
Table 6.2
Step
4
5
6
7
8
9
V1
V2
V
V
Q1
Q2
V
µC
µC
µC
µC
V
Name
:
______________________________
Matrix No
:
______________________________
-59-
Observation
Date : ______________
ENT 161 ELECTRIC CIRCUIT
ELECTRONIC BIOMEDICAL ENGINEERING
MECHATRONIC ENGINEERING SCHOOL
SEM 1, 2008/2009
6. EXERCISE
6.1 Why did the LEDs flash for a shorter time in Step 9 and Step 7 than in Step 5?
6.2 What would happen if you added more series capacitance in Step 5?
6.3 What is the total capacitance when a 1.0 µF capacitor is connected in parallel with a 2.0
µF capacitor?
6.4 If the above capacitors are connected in series, what is the total capacitance?
6.5 In the preceding series connection, which capacitor has the greater voltage across it?
Table 6.3
TIME (s)
1st
Vo (V)
2nd
3rd
Vo (Average)
5
10
20
30
40
50
60
Name
:
______________________________
Matrix No
:
______________________________
-60-
Vo/Vin
In ( Vin/Vo)
Date : ______________
ENT 161 ELECTRIC CIRCUIT
ELECTRONIC BIOMEDICAL ENGINEERING
MECHATRONIC ENGINEERING SCHOOL
SEM 1, 2008/2009
Graph 6.1
-61-
ENT 161 ELECTRIC CIRCUIT
ELECTRONIC BIOMEDICAL ENGINEERING
MECHATRONIC ENGINEERING SCHOOL
SEM 1, 2008/2009
Name
:
______________________________
Matrix No
:
______________________________
Graph 6.2
-62-
Date : ______________
ENT 161 ELECTRIC CIRCUIT
ELECTRONIC BIOMEDICAL ENGINEERING
MECHATRONIC ENGINEERING SCHOOL
SEM 1, 2008/2009
Name
:
______________________________
Matrix No
:
______________________________
Date : ______________
7. DISCUSSION
8. CONCLUSION
Based on measurement data and graph, make your overall conclusion by referring to the
objective of this experiment.
-63-
ENT 161 ELECTRIC CIRCUIT
ELECTRONIC BIOMEDICAL ENGINEERING
MECHATRONIC ENGINEERING SCHOOL
SEM 1, 2008/2009
EXPERIMENT 7
INDUCTOR
1. OBJECTIVE:
1.1. To explores RL circuit characteristic
1.2. Demonstrate the effect of frequency on inductive reactance
2. INTRODUCTION :
The self induced EMF across the inductor is E = -Ldi/dt. The following is an RL circuit.
R1 is resistor inside the power supply. R2 is used to measure the current in the circuit by
observing the voltage drop across this resistor. R3 is the resistance of the inductor
itself. Since inductors are made from many winds of wire, they all have some internal
resistance unless they are superconducting. L is the inductance of the inductor.
When the switch is suddenly closed current starts to flow, however the inductor will
generate an EMF such that the current will not flow immediately. Instead, the current
will increase from zero to the maximum value over a period of time. The growth of the
current in the circuit will depend on the inductance and the resistance in the circuit.
When the switch in the above circuit is closed, we can write Kirchoff's Law of voltages:
V0 - i(R1 + R2+ R3 ) - Ldi/dt = 0
-64-
(1)
ENT 161 ELECTRIC CIRCUIT
ELECTRONIC BIOMEDICAL ENGINEERING
MECHATRONIC ENGINEERING SCHOOL
SEM 1, 2008/2009
The solution to this equation is:
L/RT
(2)
i = [V0/RT](1 - e-t/)
RT = R1+ R2+ R3
This looks like the voltage across the capacitor of an RC circuit during the charging
phase
RL Circuit
Impedance
Contribution to
complex impedance
-65-
Phasor diagram
ENT 161 ELECTRIC CIRCUIT
ELECTRONIC BIOMEDICAL ENGINEERING
MECHATRONIC ENGINEERING SCHOOL
SEM 1, 2008/2009
3. COMPONENTS AND EQUIPMENTS:
3.1. Breadboard
- 1 Unit
3.2. DC power supply – 1 Unit
3.3. Digital Multimeter – 1 Unit
3.4. Function Generator – 1 Unit
3.5. Oscilloscope
- 1 Unit
3.6. Resistor 100kΩ
- 1 Pcs
3.7. Inductor 2.5mH
- 1 Pcs
3.8. Switch
- 1 Pcs
4. PROCEDURE (A):
4.1. Connect your DC power supply, inductor, resistor and multimeter as in Figure
7.1.
Figure 7.1
4.1.1. Let switch,S1 at point 1.
4.1.2. Adjust your power supply for a voltage of 10.0 V.
4.1.3. Simultaneously change the switch to point 2 and start your stopwatch.
4.1.4. Take measurement of Vo every 5 seconds for at least three time
constants. Record your data in Table 7.1.
4.1.5. Calculate i using Vo/ R.
-66-
ENT 161 ELECTRIC CIRCUIT
ELECTRONIC BIOMEDICAL ENGINEERING
MECHATRONIC ENGINEERING SCHOOL
SEM 1, 2008/2009
4.1.6. Plot Current (i) vs. time graph in Graph 7.1.
4.2. PROCEDURE(B):
4.2.1. Construct the circuit shown in Figure 7.2 Be sure the generator is set for
25 kHz and the output voltage is 5 Vp-p. Measure the output voltage with
the DMM. Measure the voltage across R1 and record it in the data table.
Now calculate the current through the resistor and enter it in the data table.
Next measure and record the voltage across the inductor. Finally, calculate
the reactance and enter it in the table (remember IR = IL).
Figure 7.1
4.2.2. Measure phase shift in degrees. Use time, cursors, t1, t2, set to 360
degrees, etc…Note phase difference of 2 waveforms. Check to see if the
reactance determined above agrees with the value calculated by the
reactance formula. Calculate and record the reactance using the formula XL
= 6.28fL.
4.2.3. The reactance calculated here should be within 15% of the reactance you
listed in the data table. If it is not, recheck your measurements and your
calculations.
4.2.4. Draw and label your CH1 and CH2 signal in graph 7.2
-67-
ENT 161 ELECTRIC CIRCUIT
ELECTRONIC BIOMEDICAL ENGINEERING
MECHATRONIC ENGINEERING SCHOOL
SEM 1, 2008/2009
4.2.5. Change the frequency of the generator to 50 kHz. Measure the output
voltage of the generator. Readjust the output control (if necessary) to obtain
exactly 5 vrms. You have doubled the frequency of the generator and held
the voltage constant.
4.2.6. Make the measurements and calculation necessary to complete the
second row of the data table.
4.2.7. Draw and label your CH1 and CH2 signal in graph 6.2
4.2.8. Change the generator frequency to 100 kHz. Readjust the output for 5 V if
necessary. From the reactance you determined in the first two rows of the
data table, predict and record the reactance you will have at 100 kHz.
Complete the third row of the data table. Draw and label your CH1 and CH2
signal in graph 6.2
NOTES:
1. XL1 computed from VL1 & IR1.
2. XL1 computed from XL=6.28fL
-68-
ENT 161 ELECTRIC CIRCUIT
ELECTRONIC BIOMEDICAL ENGINEERING
MECHATRONIC ENGINEERING SCHOOL
SEM 1, 2008/2009
Name
:
______________________________
Matrix No
:
______________________________
Date : ______________
5. RESULT:
Table 7.1
TIME (s)
5
10
15
20
25
30
35
-69-
1st
Vo (V)
2nd
3rd
Vo
(Average)
i=Vo/R
ENT 161 ELECTRIC CIRCUIT
ELECTRONIC BIOMEDICAL ENGINEERING
MECHATRONIC ENGINEERING SCHOOL
SEM 1, 2008/2009
Graph 7.1
Table 7.2
Frequency
Voltage across
R1
Current through
R1
Voltage across
L1
Inductive
reactance
f
VR1
IR1
VL1
XL1
(measured)
(measured)
25 kHz
50 kHz
100 kHz
Graph 7.2
25kHz
100kHz
-70-
50kHz
ENT 161 ELECTRIC CIRCUIT
ELECTRONIC BIOMEDICAL ENGINEERING
MECHATRONIC ENGINEERING SCHOOL
SEM 1, 2008/2009
Name: ______________________________
Date: ______________
Matrix No.:______________________________
6. DISCUSSION:
Based on measurement data and graph, make your overall conclusion by referring to the
objective of this experiment.
7. CONCLUSION:
-71-