Download Ann Khadaran

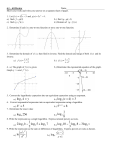
Written Assignment # 8
4.1 #4
Decide whether each function as defined or graphed is one-to-one.
See attached for graph
No, it is not one-to-one since it does not pass the horizontal line test. A
horizontal line must cross the function only once.
4.1 #12
Decide whether each function as defined or graphed is one-to-one.
y   100  x 2
No it is not one to one because x = 2 and x = -2 both map to the same value of
y. It does not pass the horizontal line test.
4.1 #16
Decide whether each function as defined or graphed is one-to-one.
y
4
x8
Yes, it is one-to-one since it passes both the vertical and horizontal line test.
Note that x = 8 is excluded from the domain since the denominator will be
zero there. You can also check this by showing that f(a) = f(b) means a = b.
-4 / (a-8) = -4 / (b-8)
1 / (a-8) = 1 / (b-8)
a–8=b–8
a=b
4.1 #40
Determine whether each pair of functions as graphed or defined are inverses
of each other.
x8
7
No they are not. Let’s show it by finding the inverse function of f(x) = 8x – 7.
y = 8x – 7. Now exchange x and y:
x = 8y – 7. Now solve for y:
8y = x + 7
y = (x + 7) / 8
f x   8x  7
g x  
f(x) = (x + 7) / 8
so g(x) as given is not the inverse function.
4.1 #50
For each function as defined that is one-to-one, (a) write an equation for the
inverse function in the form y  f 1 x  , (b) graph f and f 1 on the same
axes. And (c) give the domain and the range of f and f 1 . If the function is
not one-to-one, say so.
y  4x  5
a) x = 4 y – 5 so y = (x + 5) / 4
b)
c) The domain and range are both negative infinity to infinity
4.1 #58
For each function as defined that is one-to-one, (a) write an equation for the
inverse function in the form y  f 1 x  , (b) graph f and f 1 on the same
axes. And (c) give the domain and the range of f and f 1 . If the function is
not one-to-one, say so.
4
x
a) x = 4/y so y = 4/x. It is it’s own inverse
y
b)
c) The domain is all real numbers except 0. The range is also all real
numbers except 0.
4.2 #24
Graph each function.
f x   2 x
4.2 #46
Solve each equation.
x
9
 2
  
3
4
Take the log of both sides
log (2/3)x = log(9/4)
x log(2/3) = log(9/4)
x = log(9/4) / log(2/3) = 0.35218 / (-0.17609) = -2
You can also recognize that 9/4 = (3/2)2 = (2/3) -2
4.2 #62
Solve each equation.
z 5 /2  32
Take both sides to the 2/5 power.
z = 32 2/5 = 22 = 4
4.2 #64(a) Future Value. Find the future value and interest earned if $56,780 is invested
at 5.3% compounded.
Quarterly for 23 quarters
I presume that 5.3% is the annual interest rate. The quarterly interest is
therefore 5.3% / 4 = 1.325% = 0.01325
The future value is FV = 56780 (1+0.01325)23 = $76855.90
The interest earned is $76855.90 – 56780 = $20075.90
If this were done with the compounding formula, see below, would this be a different
answer?
r

A  P 1  

m
tm
That is the formula I used. P = 56780, r/m = 5.3%/4 = 1.325%, and tm = 23.
Technically, t = 23/4 years and m = 4 quarters per year, so tm = (23/4)*4 = 23.
4.2 #68
Interest Rate. Find the required annual interest rate to the nearest tenth of a
percent for $65,000 to grow to $65,325 if interest is compounded monthly for
6 months.
Let m be the required monthly interest rate.
65000 (1+m)6 = 65325
(1+m)6 = 1.005
1 + m = 1.005 1/6 = 1.0008316
m = 1.0008316 – 1 = 0.0008316 = 0.08316%
The annual interest rate is 12m = 12 (0.0008316) = 0.00998 = 0.998% = 1.0%
If this were done with the compounding formula, see below, would this be a different
answer?
r

A  P 1  

m
tm
That is the formula I used. A = 65325, P = 65000, tm = .5 years * 12
months/year = 6, and I’m solving for r/m, which I called m above. Then I
multiplied r/m by m=12 to get the annual interest rate.
4.3 #4
For each statement, write an equivalent statement in logarithmic form.
25  32
Ans: log 32 2  5
Reverse the 32 and 2: log 2 32 = 5
4.3 #10
For each statement, write an equivalent statement in exponential form.
log 4
1
 3
64
3
 1
Ans:    4
 64 
This is a true statement, but the usual conversion is 4 -3 = 1/64
4.3 #14
Solve each logarithmic equation.
1
81
3x = 1/81 = 1 / (34) = 3-4
x = -4
x  log 3
4.3 #28
Solve each logarithmic equation.
x  log 5 4 25
5x = 25 1/4 = 5 2/4 = 5 1/2
x = 1/2
4.3 #60
Use the properties of logarithms to rewrite each expression. Simplify the
result if possible. Assume all variables represent positive real numbers.
2 3
5
log 2 2 + log 2 31/2 – log 2 5
1 + ½ log2 3 – log2 5
log 2
4.3 #76
Given log10 2  .3010 and log10 3  .4771 , find each logarithm without using
a calculator.
20
27
log 20 – log 27
log (2 x 10) – log (33)
log 2 + log 10 – 3 log 3
0.3010 + 1 – 3(0.4771) = -0.1303
log10
4.4 #14
Use a calculator with logarithm keys to find an approximation to four decimal
places for each expression.
log .319
Ans: -.4962
This is correct.
4.4 #34
Use your calculator to find an approximation for each logarithm.
(a) log 398.4
(b) log 39.84
(c) log 3.984
(d) From your answers in parts (a) – (c), make a conjecture concerning the
decimal values in the approximations of common logarithms of numbers
greater than 1 that have the same digits.
Ans:
(a) 2.6003
(b) 1.6003
(c) .6003
(d) If the numbers greater than 1 have the same digits, then the
common logs of the numbers will have the same values following the decimal
and will differ only in the value preceding the decimal. The value preceding
the decimal of the common log will be one less than the number of digits
preceding the decimal in the original number.
4.4 #36
Use the change-of-base theorem to find an approximation for four decimal
places for each logarithm.
log 2 9
log 9
log 2
(log 9) / (log 2) = 0.9542 / 0.3010 = 3.1699
Ans:
4.4 #62
Earthquake Intensity. On June 16, 1999, the city of Puebla in central Mexico
was shaken by an earthquake that measured 6.7 on the Richter scale. Express
this reading in terms of I 0 .
The original equation is missing. Assuming there is no distance correction
factor, it is simply I = I0 10 6.7
The original equation is:
I
, where I is the
I0
amplitude registered on a seismograph 100 km from the epicenter of the
The magnitude of an earthquake, measured on the Richter scale is log10
earthquake, and I 0 is the amplitude of an earthquake of a certain (small) size.
Find the Richter scale ratings for earthquakes having eh following amplitudes.
(a) 1000I 0 (b) 1, 000, 000I 0 (c) 100, 000, 000I 0
My answer is then correct.
6.7 = log (I/I0)
10 6.7 = I/I0
I = I0 106.7 = 5011872 I0
4.5 #8
Solve each equation. When solutions are irrational, give them as decimals
correct to four decimal places.
32 x 5  13
2x – 5 = log 3 13 = 2.3347
2x = 7.3347
x = 3.6674
4.5 #20
Solve each equation. When solutions are irrational, give them as decimals
correct to four decimal places.
500 1.05   200
1.05 x/4 = 0.4
x/4 = log 1.05 0.4
x = 4 log 0.4 / (log 1.05) = -75.1209
x /4
4.5 #32
Solve each equation. When solutions are irrational, give them as decimals
correct to four decimal places.
In 2x  5   Inx  In7
ln [(2x+5) (x)] = ln 7
x (2x+5) = 7
2x2 + 5x – 7 = 0
x = -7/2 or x = 1, but x cannot be negative since logs are defined only for
positive arguments, so x = 1.
4.5 #72
Investment Time. Find t to the nearest hundredth if $1786 becomes $2063 at
2.6%, with interest compounded monthly.
0.026 / 12 = 0.0021667
2063 = 1786 (1 + 0.0021667)t
1.155095 = 1.0021667 t
t = log (1.155095) / log(1.0021667) = 66.62 months
This one is also referring to the formula:
r

A  P 1  

m
tm
A = 2063, P = 1786, r = 0.026, m = 12. I then solve for tm. You can divide
by 12 if you like to get the time in years.
4.5 #74
Interest Rate. At what interest rate will $16,000 grow to $20,000 if invested
for 5.25 yr and interest is compounded quarterly?
5.25 * 4 = 21 quarters
20000 = 16000 (1+q)21
1.25 = (1+q)21
1+q = 1.25 1/21 = 1.01068
q = 0.01068 = 1.068%
The annual interest rate is 4q = 4(1.068%) = 4.273%
This one is also referring to the formula:
r

A  P 1  

m
tm
See above.
4.6 #12
Carbon 14 Dating. A sample from a refuse deposit near the Strait of Magellan
had 60% of the carbon 14 of a contemporary living sample. How old was the
sample?
t = -t1/2 log 2 (N/N0)
t1/2 = 5730 years (approx) for carbon 14.
t = -5730 log 2 0.6 = 4220 years.
4.6 #14
Dissolving a Chemical. The amount of a chemical that will dissolve in a
solution increases exponentially as the (Celsius) temperature t is increased
according to the model A t   10e.0095t . At what temperature will 15g
dissolve?
15 = 10 e 0.0095 t
1.5 = e 0.0095 t
ln (1.5) = 0.0095 t
t = ln (1.5) / 0.0095 = 42.68 Celsius
4.6 #20
Growth of an Account. If Mrs. Blanchard (see exercise 19) chooses the plan
with continuous compounding, how long will it take for her $60,000 to grow
to $80,000?
For continuous compounding the follow formula is shown in my text.
If P dollars are deposited at a rate of interest r compounded continuously for t
years, the compound amount in dollars on deposit is A  Pert This is the
formula used in your answer, isn’t it? Just want to confirm.
Yes, that is the formula I used below.
Exercise #19
Debbie Blanchard, who is self-employed, wants to invest $60,000 in a pension
plan. One investment offers 7% compounded quarterly. Another offers
6.75% compounded continuously.
a) Which investment will earn more interest in 5 years?
b) How much more will the better plan earn?
80000 = 60000 e 0.0675 t
1.3333 = e 0.0675 t
0.0675 t = ln 1.3333 = 0.28768
t = 4.2620 years
4.6 #22
Doubling Time. If interest is compounded continuously and the interest rate
is tripled, what effect will this have on the time required for an investment to
double?
Originally: 2 P = P er t, r t = ln(2), t = ln(2)/r. So, if the interest rate triples,
the investment will double in 1/3 the time.