Download Document

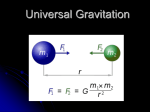
Planetary Motion and Gravitation
We now know that planets orbit the Sun in much the same way that the Moon orbits
the earth. However, in the not so distant past, we thought that all planets (including the
Sun) orbited around the Earth.
Johannes Kepler is the scientist given credit for describing the motion of the Earth,
Sun, Moon and other planetary bodies relative to each other.
He proposed three laws that represent the motion of planets around the Sun.
Kepler’s First Law: The paths of the planets are ellipses with the Sun at one of the two
focal points.
Kepler’s Second Law: An imaginary line drawn from the sun to a planet will sweep
out equal areas during equal time intervals. This law essentially explains that planets
will move faster when they are closer to the Sun than when they are farther away.
Kepler’s Third Law: The ratio of the period squared for two planets is equal to the
cube of the ratio of the average distance of the two planets from the Sun.
TA 2
=
TB
rA
rB
( ) ( )
3
Kepler’s Third Law can be used for other systems besides planets orbiting the sun. For
example, if a planet has several moons orbiting it, the moons will also obey Kepler’s
Third Law.
TA 2
rA 3
=
TB
rB
( ) ( )
Example: Planet Q has two moons orbiting it. Moon a has a period of 7.4 days and
has an average distance of 1.7X104 mi from planet Q. If Moon b has a period of 24.7
days, what is the average distance of Moon b from planet Q?
Remember that we can assign variables in whichever way makes the
problem
Click
to see easier.
Solution
With that in mind let: TA = period of Moon b = 24.7 days
TB = period of Moon a = 7.4 days
rA = radius of Moon b = ?
rB = radius of Moon a = 1.7X104 mi
Rearranging Kepler’s 3rd Law gives:
rA =
rB
( )
3
TA
TB
2
( )
3
rA =
(1.7X104
rA =
3.8X104 mi
mi)
24.7 d
7.4 d
2
See example problem and practice problems on page 174
Note: Kepler’s Laws were based on observations of actual planetary positions.
While Kepler’s Laws do accurately represent the motion of the planets around the
Sun, they do not explain why the planets and moons behave the way they do.
It was not until Sir Isaac Newton proposed the Law of Universal Gravitation that we
really understood why the planets and moons move the way they do.
The law states that the gravitational force (Fg) is equal to the universal gravitational
constant (G) times the mass of object 1 times the mass of object 2 divided by the
square of the distance between the two objects.
m1m2
Fg = G
r2
If we link Newton’s Law of Universal Gravitation with Kepler’s 3rd Law, we can
derive the formula for the period of a planet orbiting the Sun (T).
T = 2p
( )
r3
Gms
where r is the radius of the planet’s orbit
G is the universal gravitational constant
ms is the mass of the sun
Can you use the above equation to prove that it can be used to create Kepler’s 3rd Law?
Period of planet “a”
Ta = 2p
( )
ra3
Gms
Period of planet “b”
Tb = 2p
( )
rb3 to see Solution
Click
Gms
Ratio of period of planet “a” to period of planet “b”
Ta
2p
=
Tb
2p
( )
( )
ra3
Gms
rb3
Gms
Squaring both sides and canceling out terms gives
Ta 2
=
Tb
ra
rb
( ) ( )
3
In 1798 Henry Cavendish was able to actually determine the value of G
His work found that the value of G is 6.67X10-11 N∙m2/kg2
One important side result to measuring the value of G is that we can use it to
calculate the mass of the Earth (assuming that we know the radius of the Earth).
We have two related equations: one for the gravitational force between two objects
and one for the force of Earth’s gravity accelerating on an object on the Earth.
mE m
Fg = G
rE2
Fg = mg
Setting these two equations equal to each other will allow us to solve for the mass of
the Earth
grE2
mE =
= 5.98X1024 kg
G
Using the Law of Universal Gravitation Equation
NASA needs to understand the Law of Universal Gravitation Equation whenever it
wants to put a satellite into orbit.
A satellite moves in a circular orbit around Earth (assuming that is remains a
constant distance from the center of the Earth). Therefore equations relating to
centripetal acceleration will be important.
2
ac =
r
Fnet = mac
m2
Which after substitution gives: Fnet =
r
mE m
m2
Fnet = G
=
rE2
r
Solving for velocity will allow us to find the equation that relates the velocity of a
satellite to the radius of its orbit.
 =
( )
GmE
r
T = 2p
( )
r3
Gms
We can use the equation for the period of a planet
orbiting the Sun to create a general equation for any
small object orbiting a larger object.
Ts = 2p
( )
r3
Gmp
Where Ts is the period of the satellite (small object) and mp is the mass of the planet
(large object) it is orbiting and r is the radius of the orbit (note that the radius of the
orbit includes the radius of the planet and the height of the satellite above the
surface of the planet).
Example: If we want to make a satellite orbit the Earth at a distance of 155 km above
the surface of the Earth, how fast will we need to make the satellite travel and what
will the period of the satellite be at this location?
We will need equations being discussed on the last two slides. In addition, we will
Click to see Solution
need the value of G, mE and rE.
 =
( )
GmE
r
G = 6.67X10-11 Nm2/kg2
( )
r3
Gmp
Ts = 2p
mE = 5.97X1024 kg
rE = 6.38X106 m
r = rE + 1.55X105 m = 6.38X106 m + 1.55X105 m = 6.535X106 m
 =
(
Ts = 2p
(6.67X10−11 Nm2/kg2)(5.97X1024 kg)
6.535X106 m
(
)
(6.535X106 m)3
(6.67X10−11 Nm2/kg2)(5.97X1024 kg)
 = 7806 m/s = 7810 m/s
)
See Example Problem and Practice Problems on page 181
Ts = 5,260 s = 1.46 h
By manipulating some of the equations we have been working with we can create
equations that have new meaning to us.
mE m
Fnet = G
= ma
r2
Equation for any free falling object near Earth’s surface.
Near Earth’s surface, a = g and r = rE so
mE
g= G 2
rE
mE
or a = G 2
r
Significantly above Earth’s surface, a ≠ g and r ≠ rE so rearranging and
substituting for mE will give:
ah = g
rE 2
r
()
where ah is the acceleration due to gravity at some
significant distance above Earth’s surface
Note that r = rE + h so the acceleration due to gravity will get smaller as the
distance from Earth increases.
Find the acceleration due to gravity at an distance of 500 km from Earth’s surface.
Have you ever experienced weightlessness?
Remember that Weight and Mass are two very different things. Mass is the amount
of matter and has units of g or kg. Weight is a field force (see page 94) on a mass
due to gravity and has units of N. Therefore an object’s Weight depends upon
gravity.
However, there are many situations where our apparent weight depends not only
upon gravity but also upon the motion we are experiencing.
When an elevator starts to move, your apparent weight briefly changes. You feel
heavier if the elevator is accelerating upward and you feel lighter than normal if the
elevator is accelerating downward. Can you think of other similar situations?
An extreme version of this is the weightlessness that astronauts feel when they are in
orbit around the Earth. Note that while in orbit around Earth, the acceleration due to
gravity (g) is almost the same size as it is on the surface of the Earth. If the change
in the acceleration due to gravity is not the cause of the feeling of weightlessness,
what is?
Gravitational Field
A gravitational field is created by all objects having mass. The mass of the
object will attract other objects toward it from any direction (a spherical field).
The strength of the gravitational field (g) depends upon the mass of object A
creating the field and the distance you are from the center of mass as shown by
the equation below.
mA
g= G 2
r
The force exerted on an object B in the field will be the object B’s mass times
the strength of the gravitational field.
F = mBg
Note that the “m” in the two equations represent different masses. The “mA” in
the first equation is the mass of object A (the object that is creating the
gravitational field, usually thought of as being the larger mass of the two objects)
while the “mB” is the mass of object B (the object that is experiencing the
gravitational field. (In reality all objects create a gravitational field, but we usually
look at the problem from the perspective of the larger mass).
The gravitational field that is created by an object will attract any mass near it.
The shorter the distance between the two objects, the stronger the force of attraction.
The larger the masses of the objects, the stronger the force of attraction.
When we think of a planet orbiting the Sun, we usually think that the Sun is directly
attracting the planet, but the reality is more that the gravitational field of the Sun
interacts with the mass of the planet and this is what causes the planet to be attracted
toward the Sun.
Note that the gravitational field of the planet is also attracting the Sun, but since the
Sun has so much more mass than the planet, the planet is thought of as being the
object that moves toward the Sun and not the other way around.
Note that the symbol “g” being used for the gravitational field is the same as the “g”
we used for the acceleration due to gravity (9.80 m/s2) but the meaning is a little
different. The acceleration due to gravity is a vector quantity showing how an
object in another object’s gravitational field will be accelerated but the gravitational
field is acting over all of space and will be oriented toward the center of mass of the
object creating the field and changes with the distance from the center of mass.
Inertial Mass and Gravitational Mass
Inertial Mass is the definition of mass based on the amount of force required to
accelerate an object.
Gravitational Mass is the definition of mass based on the force of gravity acting on
an object.
We can write the equations for Inertial Mass and Gravitational Mass by rearranging
two existing equations as shown below.
Fnet= minertiala
minartial =
Fnet
a
mgravm
Fgrav = G
r2
r2Fgrav
mgrav =
Gm
Newton proposed the idea that these two ways of defining mass are the same. So far,
all experiments support this idea.
However, there may still be more to the story. Einstein proposed that gravity is not a
force but instead is a result of the way mass effects space itself.
According to Einstein, mass causes space to be curved instead of flat. The more
massive the object, the greater the curvature of space.
What could be a possible consequence of this idea?
For ordinary objects (like planets orbiting the Sun), Einstein’s idea gives the same
results as Newton’s idea.
For Newton, gravity attracts the planet toward the Sun and for Einstein the planet
will be following a curved path around the Sun that is created by the way that the
Sun curves space around it.
However, Einstein’s idea predicts that light should follow a curved path as it travels
past a very massive object while Newton’s idea would predict that light would
travel in a straight line.
See Figures 7-15 and 7-16 on pages 184 and 185 respectively for illustrations of
Einstein’s idea about gravity and space.