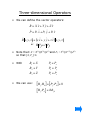Download Lecture 24: Tensor Product States

Lecture 24:
Tensor Product States
Phy851 Fall 2009
Basis sets for a particle in 3D
• Clearly the Hilbert space of a particle in three
dimensions is not the same as the Hilbert
space for a particle in one-dimension
• In one dimension, X and P are incompatible
– If you specify the wave function in coordinatespace, 〈x|ψ〉, its momentum-space state is
completely specified as well:
〈p|ψ〉 =∫dx〈p|x〉〈x|ψ〉
– You thus specify a state by assigning an
amplitude to every possible position OR by
assigning and amplitude to every possible
momentum
ψ ( x) = x ψ
or
ψ ( p) = p ψ
• In three dimensions, X, Y, and Z, are
compatible.
– Thus, to specify a state, you must assign an
€ position in three
amplitude to each possible
dimensions.
– This requires three quantum numbers
ψ ( x, y , z ) = x, y , z ψ
– So apparently, one basis set is:
{ x, y,z }
∃ x, y,z ∀ (x, y,z) ∈ R 3
Definition of Tensor product
• Suppose you have a system with 10 possible
states
• Now you want to enlarge your system by
adding ten more states to its Hilbert space.
– The dimensionality of the Hilbert space increases
from 10 to 20
– The system can now be found in one of 20
possible states
– This is a sum of two Hilbert sub-spaces
– One quantum number is required to specify
which state
• Instead, suppose you want to combine your
system with a second system, which has ten
states of its own
– The first system can be in 1 of its 10 states
– The second system can be in 1 of its 10 states
• The state of the second system is independent of
the state of the first system
– So two independent quantum numbers are
required to specify the combined state
• The dimensionality of the combined Hilbert
space thus goes from 10 to 10x10=100
– This combined Hilbert space is a
(Tensor) Product of the two Hilbert sub-spaces
Formalism
• Let
H1 and H2 be two Hilbert spaces
– We will temporarily ‘tag’ states with a label to
specify which space the state belongs to
ψ
(1)
∈ H1
• Let the Hilbert space
product of spaces
( 2)
φ
H12
∈ H2
be the tensor-
H1 and H2 .
H 12 = H 1 ⊗ H 2 H12 is the ‘tensor product’
of H1 and H2
• The Tensor product state |ψ12〉=|ψ1〉(1) ⊗|ψ2〉(2)
belongs to H12.
• The KEY POINT TO ‘GET’ IS:
– Bras and kets in the same Hilbert space
‘attach’.
ψ1
(1)
→ ← ψ2
(1)
⇒
ψ1 ψ 2
– BUT, Bras and kets in different Hilbert
spaces do not ‘attach’
ψ1
(1)
→ ← ϕ1
( 2)
⇒
ϕ1
( 2)
ψ1
(1)
They just slide past
each other
Schmidt Basis
• The easiest way to find a good basis for a
tensor product space is to use tensor products
of basis states from each sub-space
If:
H1
{|n2〉(2) } ; n2=1,2,…,N2 is a basis in H2
{|n1〉(1) } ; n1=1,2,…,N1 is a basis in
It follows that:
{|n1, n2〉(12) }; |n1, n2〉(12)=|n1〉(1)⊗|n2〉(2) is a basis in
If System 1 is in state:
ψ1
(1)
N1
= ∑ an1 n1
H12.
(1)
n1 =1
and System 2 is in state: ψ 2
( 2)
N2
= ∑ bn2 n2
( 2)
n2 =1
Then the combined system is in state:
ψ1,ψ 2
(12)
= ψ1
(1)
⊗ ψ2
(2)
N1
N2
= ∑ ∑ an1 bn 2 n1,n 2
(12)
n1 =1n 2 =1
• Schmidt Decomposition Theorem:
€
All states in a tensor-product space can be
expressed as a linear combination of tensor
product states
N N
ψ 12
(12 )
1
2
= ∑ ∑ cn1n2 n1, n2
n1 =1 n2 =1
(12 )
Entangled States
• The essence of quantum `weirdness’ lies in
the fact that there exist states in the tensorproduct space of physically distinct systems
that are not tensor product states
• A tensor-product state is of the form
ψ
(12 )
= ψ1
(1)
⊗
ψ2
( 2)
– Tensor-product states are called ‘factorizable’
• The most general state is
ψ 12
(12 )
N1
N2
= ∑ ∑ cn1n2 n1, n2
(12 )
n1 =1 n2 =1
– This may or may-not be ‘factorizable’
• Non-factorizable states are called ‘entangled’
– For an `entangled state’, each subsystem has no independent objective
reality
Configuration Space
• The state of a quantum system of N
particles in 3 dimensions lives in
‘configuration space’ (We don’t know about spin yet)
– There are three quantum numbers
associated with each particle
• It takes 3N quantum numbers to specify a
state of the full system
– Coordinate Basis:
{ x1, y1,z1, x 2, y 2 ,z2,..., x N , y N ,zN }
or we could just write
€
r r
r
{ r1, r2,..., rN
– Wavefunction:
}
This form is the
coordinate system
independent
representation
r r
r
r r
r
€
ψ (r1 , r2 ,..., rN ) = r1 , r2 ,..., rN ψ
– To specify a state of N particles in d
dimensions requires d·N quantum
numbers
So counting quantum numbers might be a good
way to check if you are using a valid basis
Tensor Products of Operators
• THEOREM:
Let A (1) act in
H1 , and B(2) act in H2 ,
Then the tensor product operator C(12) =A(1)⊗ B(2)
acts in H12 .
• PROOF:
A(1) = ∑ am am
(1)
am
(1)
B ( 2 ) = ∑ bm bm
( 2)
bm
( 2)
m
m
A(1) ⊗ B (2) = ∑ am bn am
(1)
am
(1)
(2)
bn
⊗
bn
(2)
m,n
(
= ∑ am bn am
m,n
€
(1)
⊗
(12 )
C (12 ) = ∑ ambn am , bn
bn
(2)
)(
am , bn
am
(1)
⊗
bn
(2)
(12 )
m,n
€
• The action of C(12) on a tensor-product state:
ψ 1 ,ψ 2
C
(12 )
ψ 1 ,ψ 2
(12 )
(12 )
:= ψ 1
(1)
= ∑ ambn am , bn
m,n
⊗
(12 )
ψ2
( 2)
am ψ 1
(1)
bn ψ 2
( 2)
)
General form of Operators in
Tensor-product spaces
• The most general form of an operator in
is:
C (12 ) = ∑ cm ,n;m ',n ' m, n
(12 )
m' , n'
H12
(12 )
m,n
cm ,n;m ',n ' := m, n
(12 )
C (12 ) m′, n′
(12 )
– Here |m,n〉 may or may not be a tensor
product state. The important thing is that
it takes two quantum numbers to specify
a basis state in H12
• A basis that is not formed from tensorproduct states is an ‘entangled-state’ basis
• In the beginning, you should always start
with a tensor-product basis as your ‘physical
basis’
– Then all operators are well-defined
– Just expand states and operators onto tensorproduct states
– Then match up the bras and kets with their
proper partners when taking inner products
Upgrading Subspace Operators
• Any operator in
H1
can be upgraded to an
H12 by taking the tensor product
with the identity operator in H2 :
operator in
A(12 ) = A(1) ⊗ I ( 2 )
– If A1 is an observable in H1, then it is also an
observable in H12 (since it remains Hermitian
when upgraded).
– The spectrum of A1 remains the same after
upgrading
Proof:
Let
A(1) am
(1)
= am am
(1)
Then:
(
A(1) ⊗ I (2) am
(1)
⊗ψ
(2)
) (
(1)
= A(1) am
= am am
(
= am am
(1)
€
⊗ψ
(1)
Note that |ψ2〉 is completely
) (
⊗ I
⊗
arbitrary, but |a1〉⊗|ψ2〉 is an
eigenstate of A(12)
(2)
ψ
(2)
ψ
(2)
)
(2)
)
Product of two Upgraded Operators
• Let A(1) and B(2) be observables in their
respective Hilbert spaces
• Let A(12)= A(1)⊗ I(2) and B(12)= I(1)⊗ B(2) .
• The product A(12)B(12) is given by A(1) ⊗ B(2)
– Proof:
( A1 ⊗ I2 )( I1 ⊗ B2 ) = A1I1 ⊗ I2 B2
= A1 ⊗ B2
€
Compatible observables
• Let A(1) and B(2) be observables in their
respective Hilbert spaces
• Let A= A(1)⊗ I(2) and B= I(1)⊗ B(2) .
• Theorem: [A,B]=0
Proof:
[A, B]= AB − BA
= (A1 ⊗ I 2 )(I1 ⊗ B2 )− (I1 ⊗ B2 )(A1 ⊗ I 2 )
= (A1 I1 )⊗ (I 2 B2 )− (I1 A1 )⊗ (B2 I 2 )
= A1 ⊗ B2 − A1 ⊗ B2 = 0
• Conclusion: any operator in
H1 , is ‘compatible’
with any operator in H2 ,.
• I.e. simultaneous eigenstates exist.
– Let A1 |a1〉= a1 |a1〉 and B2 |b2〉= b2 |b2〉.
– Let a= a1 and b= b2
– Let |ab〉= |a1〉 ⊗ |b2〉.
– Then AB|ab〉=ab|ab〉.
‘And’ versus ‘Or’
• The tensor product correlates with a system
having property A and property B
– Dimension of combined Hilbert space is product
of dimensions of subspaces associated with A
and B
– Example: start with a system having 4 energy
levels. Let it interact with a 2 level system. The
Hilbert space of the combined system has 8
possible states.
• Hilbert spaces are added when a system can
have either property A or property B
– Dimension of combined Hilbert space is sum of
dimensions of subspaces associated with A and
B
– Example: start with a system having 4 energy
levels. Add 2 more energy levels to your model,
and the dimension goes from 4 to 6
Example #1 : Particle in Three Dimensions
• Let H1 be the Hilbert space of functions
in one dimension
– The projector is: I1 = dx x x
∫
– So a basis is:
{x }
€
• Then H3= (H1)3 would then be the
Hilbert space of square integrable
€
functions in three dimensions.
– Proof: I3 = I1 ⊗ I1 ⊗ I1
∫ dx x x ⊗ ∫ dy y y ⊗ ∫ dz z z
= ∫ dxdydz x x ⊗ y y ⊗ z z
= ∫ dxdydz( x ⊗ y ⊗ z )( x ⊗ y ⊗ z )
= ∫ dxdydz x, y,z x, y,z
=
x, y , z ≡ x ⊗ y ⊗ z
€
ψ ( x, y , z ) = x, y , z ψ
ψ = ∫ dxdydz x, y, z ψ ( x, y, z )
• Note: H3 is also the Hilbert space of
three particles in one-dimensional space
Three-dimensional Operators
• We can define the vector operators:
r
R = X xˆ + Y yˆ + Z zˆ
r
P = Px xˆ + Py yˆ + Pz zˆ
r
R x, y, z = (x xˆ + y yˆ + z zˆ ) x, y, z
rr rr
or R r = r r
• Note that: X = X(1)⊗I(2) ⊗I(3) and Py = I(1)⊗P (2) ⊗I(3)
so that [X, Py]=0.
• With
€
R1 = X
P1 = Px
R2 = Y
P2 = Py
R3 = Z
P3 = Pz
• We can use:
€
[R ,R ] = [P ,P ] = 0
[R ,P ] = ihδ
j
k
j
k
j
k
jk
Example #2: Two particles in One
Dimension
• For two particles in one-dimensional space,
the Hilbert space is (H1 )2.
x1 , x2 = x1
(1)
⊗ x2
( 2)
ψ ( x1 , x2 ) = x1 , x2 ψ
I=
∫ dx dx
1
2
x1, x 2 x1, x 2 = 1
X1 = X1 ⊗ I2
P2 = I1 ⊗ P2
€
etc...
[ X , X ] = [P ,P ] = 0
[ X ,P ] = ihδ
j
j
€
k
k
j
k
jk
Hamiltonians
• One particle in three dimensions:
– Each component of momentum contributes
additively to the Kinetic Energy
1
H=
Px2 + Py2 + Pz2 + V ( X , Y , Z )
2m
v
1 r r
=
P ⋅ P + V ( R)
2m
(
)
• Two particles in one dimension:
P12
P22
H=
+
+ V ( X1, X 2 )
2m1 2m2
Conclusions
• The ‘take home’ messages are:
– The combined Hilbert space of two
systems, dimensions d1 and d2, has
dimension d1⊗2=d1·d2
– A physical basis set for the combined
Hilbert space, H1⊗2 can be formed by
taking all possible products of one basis
state from space H1 with one basis state
from H2.
{
n1
(1)
}
⊇ H 1,
n1,n 2 := n1
∴ { n1,n 2
(1)
{
n2
⊗ n2
(2)
}⊇ H
2
(2)
} ⊇ H 12 := H 1 ⊗ H 2
– In a tensor product space, a bra from one
subspace can only attach to a ket from
€
the same (1subspace:
)
(1)
ψ1
ψ1
→ ← ψ2
(1)
→ ← ϕ1
( 2)
⇒
ψ1 ψ 2
⇒
ϕ1
( 2)
ψ1
(1)
– For N particles (spin 0) in d dimensions,
d·N quantum numbers are required to
specify
in any basis
r r a unit-vector
r
r1 , r2 , K rN
n1x , n1 y , n1z , n2 x , n2 y , n2 z , K , nNx , nNy , nNz