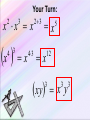* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download Lesson 3.1 Powerpoint - peacock
History of logarithms wikipedia , lookup
Large numbers wikipedia , lookup
Big O notation wikipedia , lookup
Mathematics of radio engineering wikipedia , lookup
History of the function concept wikipedia , lookup
Function (mathematics) wikipedia , lookup
Elementary mathematics wikipedia , lookup
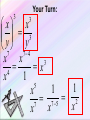
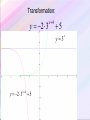
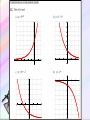
Exponential Functions and Their Graphs Section 3.1 Objectives: • Recognize and evaluate exponential functions with base a. • Graph exponential functions with base a. • Recognize, evaluate, and graph exponential functions with base e. Exponential Function An exponential function is a function of the form f(x) = ax where a is a positive number and a 1. Example: Graph f(x) = 2x. y x f(x) 2 1 4 1 2 4 0 1 2 1 2 1 2 x 4 –2 2 Exponential Functions y = 2x y = 3x y = 2x-3 - 8 y = 1 - ex Exponential Functions y = x2 y = x3 y = x5 - 3x2 + x y = 6 – 5x + x2 Power Functions Not Exponential Evaluating Exponential Functions The value of f(x) = 3x when x = 2 is f(2) = 32 =9 The value of f(x) = 3x when x = –2 is f(–2) = 3–2 1 = 9 The value of g(x) = 0.5x when x = 4 is g(4) = 0.54 =0.062 5 Graph of Exponential Function (a > 1) The graph of f(x) = ax, a > 1 y 4 Range: (0, ) (0, 1) x 4 Domain: (–, ) Horizontal Asymptote y=0 Graph of Exponential Function (0 < a < 1) The graph of f(x) = ax, 0 < a < 1 y 4 Range: (0, ) Horizontal Asymptote y=0 (0, 1) x 4 Domain: (–, ) Characteristics of Exponential Functions 1. 2. 3. 4. 5. 6. The domain of f (x) = ax consists of all real numbers. The range of f (x) = ax consists of all positive real numbers. The graphs of all exponential functions pass through the point (0, 1) because f (0) = a0 = 1. If a > 1, f (x) = ax has a graph that goes up to the right and is an increasing function. If 0 < a < 1, f (x) = ax has a graph that goes down to the right and is a decreasing function. f (x) = ax is a one-to-one function and has an inverse that is a function. The graph of f (x) = ax approaches but does not cross the x-axis. The x-axis is a horizontal asymptote. f (x) = ax 0<a<1 f (x) = ax a>1 Graphs of Exponential Functions Graph of ya y 6 0<a<1 5 x a>1 4 Exponential Decay Exponential Growth 3 2 1 x -1 -2 -3 -4 Changing the base of ax, when a>1 Changing the base of ax, when 0<a<1 Exponential Function – Change of Base Summary • For a>1, as a increases the curve moves closer to the y-axis. The y-intercept (0,1) does not change. Y=3x Y=2x Exponential Function – Change of Base Summary • For 0<a<1, as a decreases the curve moves closer to the y-axis. The y-intercept (0,1) does not change. Y=(1/3)x Y=(1/2)x PROPERTIES OF EXPONENTS The Product Rule Product Rule for Exponents If a is a real number and m and n are natural numbers, then am · an = am + n Example: Evaluate each expression: a.) c4 · c5 = c4 + 5 = c9 b.) 3a3 · a6 = 3a3 + 6 = 3a9 c.) 4w2 · 2w5 = (4)(2)w2 + 5 = 8w7 Power Rule for Exponents Power Rule for Exponents If a is a real number and m and n are natural numbers, then a m n a mn Example: Simplify each expression: a.) (25)3 = 25·3 = 215 b.) (y3)3 = y3·3 = y9 Product to a Power Rule for Exponents Product to a Power Rule for Exponents If a and b are real numbers and n is a natural number, then n a b a n bn Example: Simplify each expression: a.) (3c2)2 = (3)2(c2)2 = 9c4 b.) (– 2y5)3 = (– 2)3(y5)3 = – 8y15 Rules for Multiplying Monomials Rules for Multiplying Monomials Product Rule For Exponents If a is a real number and m and n are natural numbers, then am · an = am + n Power Rule For Exponents If a is a real number and m and n are natural numbers, then a a m n mn Product to a Power Rule For Exponents If a and b are real numbers and n is a natural number, then a b an bn n Multiply a Monomial by a Monomial Example: Multiply and simplify: a.) (5x2)(6x4) b.) (2p3)(–5p2) = 5 • 6 • x2 • x2 = 30x2 + 4 = 30x6 = 2 • (–5) • p3 • p2 = –10p3 + 2 = –10p5 The Quotient Rule The Quotient Rule for Exponents If a is a real number and if m and n are positive integers, then a m a mn an if a 0 Example: Simplify each expression. 6 a.) 32 362 34 3 y 7 y 74 y 3 b.) 4 y Remember that the base does not change. The Quotient to a Power Rule Quotient to a Power Rule for Exponents a b n n a n b if b 0. Example: Simplify each expression: 10 x x 10 y y 10 a.) b.) 3 4 3a 2 b 3 a 4 3 4 b 2 4 12 81 a 8 b Zero Exponent If a is a nonzero real number (that is, a 0), we define a0 = 1 Example: Simplify each expression. a.) b.) (24ab)0 1 3 0 3a 2 1 b Negative Exponent If n is a positive integer and if a is a nonzero real number (that is, a 0), then we define a n 1n a Example: Simplify each expression. a.) (4) 2 1 1 (4)2 16 b.) (ab) 3 1 1 (ab)3 a 3b3 Negative Exponent If a and b are real numbers and n is an integer, then a b n n b a if a 0, b 0 Example: Simplify each expression. a.) 3 x 2 5 b.) x 3 2 5 2 x 9 5 5 xy x y ab xy ab a5b5 Simplifying Expressions How to Simplify Expressions Using the Product Rule and the Negative Exponent Rule Step 1: Rearrange the factors. Step 2: Find each product. Step 3: Simplify. Write the product so that the exponents are positive. Example: Simplify the expression: 2a3b4 6a 2b 2a3b4 6a 2b 2(6) a3 a 2 b4 b Rearrange factors. 12a1b3 12a b3 Find each product. Simplify. Simplifying Expressions How to Simplify Expressions Using the Quotient Rule and the Negative Exponent Rule Step 1: Write the quotient as the product of factors. Step 2: Find each quotient. Step 3: Simplify. Write the quotient so that the exponents are positive. Example: Simplify the expression: 12 x 2 y 5 12 x 2 y 5 4 4 8 x y 8x y 3 x 2 y 4 2 3y4 2 2x 12 x 2 y 5 8x4 y Write the quotient as products. Find each quotient. Simplify. Simplifying Expressions How to Simplify Expressions Using the Power Rule and the Negative Exponent Rule Step 1: Write the quotient as the product of factors. Step 2: Find each product. Step 3: Simplify. Write the product so that the exponents are positive. 20a 3b5 Example: Simplify the expression: 4a 6b 2 2 20a b 20 a 3 b5 4 6 6 b a 4 a b 2 4 5b9 a 2 18 a9 a 4 25b8 5b 3 5 2 Write the quotient as products. Find each product. Simplify. Summary - Laws of Exponents 1. x x x m 3. x m n m n mn 2. xy x y m m x mn x mn 5. n x x m x x 4. m y y m m Other Properties of Exponents 1 x x x 1 1 0 Any single number or variable is always to the first power 33 1 aa 1 2 x 2 x 2 x 1 1 1 Your Turn: x x x 2 x 4 3 3 x 43 2 3 x x xy 5 12 3 x y 3 3 Your Turn: 3 x x 3 y y 7 74 x x 3 x 4 x 1 5 1 1 x 2 7 5 7 x x x 3 Your Turn: 2a 3 7 a 4 2 7a 34 14a 7 5r 2 8r 3 2r 2 5 8 2r 23 2 80r 7 2m n 2 5 3 3xy 3 13 23 53 2 m n 2 m n 8m n 3 3 x y 27 x y 3 3 3 3 6 15 6 15 3 2 2 2 2 2 a 2 a 4 a 2 2 2 9b 3b 3 b 8 x 4 8 x 41 4x 3 2x 2 1 9z3 9 1 3 1 3 2 2 53 5 x x 3z 3z Your Turn: 3x 3 y 2 z 7 xyz2 3 7x31 y 21 z1 2 21x 4 y 3 z 3 8xy2 3xy 2 xy3 8 3 2x111 y 213 48x 3 y 6 3x y 2 xy 2 3 2 2 2 312 x 22 y 32 212 x12 y 22 9 x 4 y 6 4 x 2 y 4 9 4x 4 2 y 6 4 36 x 6 y10 3 5a b 513 a 33b13 53 a 9b 3 125a 9b 3 125a 93 125a 6 13 13 23 3 3 6 6 3 3 6 3 2 3 a b 27 b 3 a b 27 a b 27 b 3 ab 3 Transformations Involving Exponential Functions Transformation Equation Description Horizontal translation g(x) = bx-c • Shifts the graph of f (x) = bx to the left c units if c < 0. • Shifts the graph of f (x) = bx to the right c units if c > 0. Vertical stretching or shrinking g(x) = c bx Multiplying y-coordintates of f (x) = bx by c, • Stretches the graph of f (x) = bx if c > 1. • Shrinks the graph of f (x) = bx if 0 < c < 1. Reflecting g(x) = -bx g(x) = b-x • Reflects the graph of f (x) = bx about the x-axis. • Reflects the graph of f (x) = bx about the y-axis. Vertical translation g(x) = bx + c • Shifts the graph of f (x) = bx upward c units if c > 0. • Shifts the graph of f (x) = bx downward c units if c < 0. Example Use the graph of f (x) = 3x to obtain the graph of g(x) = 3 x+1. Solution Note that the function g(x) = 3x+1 has the general form g(x) = bx-c, where c = 1. Because c < 0, we graph g(x) = 3 x+1 by shifting the graph of f (x) = 3x one unit to the left. g(x) = 3x+1 (-1, 1) -5 -4 -3 -2 -1 f (x) = 3x (0, 1) 1 2 3 4 5 6 Transforming Exponential Functions • Describe how to transform the graph of f(x)=2x into the graph of g(x). g ( x) 2 x 1 Solution: Transformation of x 2 to 2 x1 Transforming Exponential Functions • Describe how to transform the graph of f(x)=2x into the graph of h(x). h( x ) 2 x Solution: Transformation of x 2 to 2 x Reflected about y-axis y2 x This equation could be rewritten in a different form: y2 x 1 1 x 2 2 x So if the base of our exponential function is between 0 and 1 (which will be a fraction), the graph will be decreasing. It will have the same domain, range, intercepts, and asymptote. Two ways to write a decay function; 1. Base is a fraction 2. Negative exponent State “exponential growth” or “exponential decay” a.) y = e2x k > 0, exponential growth c.) y = 2–x b>1 so growth, but reflect over y-axis, so decay b.) y = e–2x k < 0, exponential decay d.) y = 0.6–x 0<b<1 so decay, but reflect over y-axis, so growth Transforming Exponential Functions • Describe how to transform the graph of f(x)=2x into the graph of k(x). k ( x) 3 2 x Solution: Transformation of 2 to 3 2 x x y2 All of the transformations that you learned apply to all functions, so what would the graph of look like? x x y 2 3 up 3 right 2 up 1 Reflected over x axis y 1 2 x down 1 y2 x2 1 Your Turn: Sketch a graph using transformation of the following: 1. f ( x) 2 x 3 2. f ( x) 2 x 1 3. f ( x) 4 x 1 1 The order of transformations: horizontal, reflection (horz., vert.), vertical. Transformation of Exponential Function • What are the effects of a, c and d in the transformation of the exponential function • Example: y a b xc y 2 3 d x4 5 Transformation: y 2 3 x4 5 y 3 y 2 3x 4 5 x Transformations • Exponential graphs, like other functions we have studied, can be dilated, reflected and translated. • It is important to maintain the same base as you analyze the transformations. g ( x) 2 3 x Vertical shift up 3 g ( x ) 3(2 x ) 1 Reflect @ x-axis Vertical stretch 3 Vertical shift down 1 Your Turn: y (2) x 1 1 Horizontal shift right 1. Reflect about the x-axis. y (3) 1 2 x2 3 Horizontal shift left 2. Vertical shrink ½ . Vertical shift up 1. Vertical shift down 3. Summary of Transformations f(x) = Reflection over the x-axis Vertical Stretch by factor of a ±x-c ±a·b +d Base Horizontal translation by of c units(opposite direction of sign) Reflection over the y-axis (neg. x makes decay curve out of growth curve) Vertical translation by of d units(same direction of sign) y = d equation of horizontal asymptote The Natural Base e An irrational number, symbolized by the letter e, appears as the base in many applied exponential functions. This irrational number is approximately equal to 2.72. The number e is called the natural base. The function f (x) = ex is called the e natural exponential function.2.71828... f (x) = 3x f (x) = ex 4 f (x) = 2x (1, 3) 3 (1, e) 2 (1, 2) (0, 1) -1 1 The Natural Base e • Represented by e to honor Euler who discovered the number. e 2.718...... Transforming Exponential Functions Your Turn: f ( x) 3e x 2 f x e x 1 Vertical stretch 3. Reflect @ x-axis. Vertical shift up 2. Vertical shift down 1. f x ex2 2 Horizontal shift left 2. Vertical shift up 2 Assignment • Pg. 193 – 195; 5 – 16 all, 17 – 21 odd