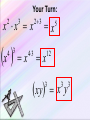Download Lesson 3.1 Powerpoint - peacock

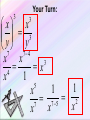
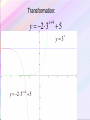
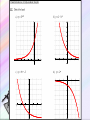
Exponential Functions
and Their Graphs
Section 3.1
Objectives:
• Recognize and evaluate exponential
functions with base a.
• Graph exponential functions with base a.
• Recognize, evaluate, and graph
exponential functions with base e.
Exponential Function
An exponential function is a function of the form
f(x) = ax
where a is a positive number and a  1.
Example:
Graph f(x) = 2x.
y
x
f(x)
2
1
4
1
2
4
0
1
2
1
2
1
2
x
4
–2
2
Exponential Functions
y = 2x
y = 3x
y = 2x-3 - 8
y = 1 - ex
Exponential
Functions
y = x2
y = x3
y = x5 - 3x2 + x
y = 6 – 5x + x2
Power Functions
Not Exponential
Evaluating Exponential Functions
The value of f(x) = 3x when x = 2 is
f(2) = 32 =9
The value of f(x) = 3x when x = –2 is
f(–2) =
3–2
1
=
9
The value of g(x) = 0.5x when x = 4 is
g(4) = 0.54 =0.062
5
Graph of Exponential Function (a > 1)
The graph of f(x) = ax, a > 1
y
4
Range: (0, )
(0,
1)
x
4
Domain: (–, )
Horizontal Asymptote
y=0
Graph of Exponential Function (0 < a < 1)
The graph of f(x) = ax, 0 < a < 1
y
4
Range: (0, )
Horizontal Asymptote
y=0
(0,
1)
x
4
Domain: (–, )
Characteristics of Exponential
Functions
1.
2.
3.
4.
5.
6.
The domain of f (x) = ax consists of all real numbers. The range of f (x) = ax
consists of all positive real numbers.
The graphs of all exponential functions pass through the point (0, 1) because
f (0) = a0 = 1.
If a > 1, f (x) = ax has a graph that goes up to the right and is an increasing
function.
If 0 < a < 1, f (x) = ax has a graph that goes down to the right and is a
decreasing function.
f (x) = ax is a one-to-one function and has an inverse that is a function.
The graph of f (x) = ax approaches but does not cross the x-axis. The x-axis
is a horizontal asymptote.
f (x) = ax
0<a<1
f (x) = ax
a>1
Graphs of Exponential
Functions
Graph of
ya
y
6
0<a<1
5
x
a>1
4
Exponential Decay
Exponential Growth
3
2
1
x






-1
-2
-3
-4




Changing the base of ax, when a>1
Changing the base of ax, when 0<a<1
Exponential Function – Change of
Base Summary
• For a>1, as a increases the curve moves closer to the y-axis.
The y-intercept (0,1) does not change.
Y=3x
Y=2x
Exponential Function – Change of
Base Summary
• For 0<a<1, as a decreases the curve moves closer to the
y-axis. The y-intercept (0,1) does not change.
Y=(1/3)x
Y=(1/2)x
PROPERTIES OF EXPONENTS
The Product Rule
Product Rule for Exponents
If a is a real number and m and n are natural numbers, then
am · an = am + n
Example:
Evaluate each expression:
a.) c4 · c5
= c4 + 5 = c9
b.) 3a3 · a6
= 3a3 + 6 = 3a9
c.) 4w2 · 2w5 = (4)(2)w2 + 5 = 8w7
Power Rule for Exponents
Power Rule for Exponents
If a is a real number and m and n are natural numbers, then
 
a
m
n
 a mn
Example:
Simplify each expression:
a.) (25)3 = 25·3 = 215
b.) (y3)3
= y3·3 = y9
Product to a Power Rule for Exponents
Product to a Power Rule for Exponents
If a and b are real numbers and n is a natural number, then
 
n
a  b  a n  bn
Example:
Simplify each expression:
a.) (3c2)2
= (3)2(c2)2 = 9c4
b.) (– 2y5)3 = (– 2)3(y5)3 = – 8y15
Rules for Multiplying Monomials
Rules for Multiplying Monomials
Product Rule For Exponents
If a is a real number and m and n are natural numbers, then
am · an = am + n
Power Rule For Exponents
If a is a real number and m and n are natural numbers, then
a   a
m
n
mn
Product to a Power Rule For Exponents
If a and b are real numbers and n is a natural number, then
a  b  an  bn
n
Multiply a Monomial by a Monomial
Example:
Multiply and simplify:
a.) (5x2)(6x4)
b.) (2p3)(–5p2)
= 5 • 6 • x2 • x2 = 30x2 + 4 = 30x6
= 2 • (–5) • p3 • p2 = –10p3 + 2 = –10p5
The Quotient Rule
The Quotient Rule for Exponents
If a is a real number and if m and n are positive integers, then
a m  a mn
an
if a  0
Example: Simplify each expression.
6
a.) 32  362  34
3
y 7  y 74  y 3
b.) 4
y
Remember that the base
does not change.
The Quotient to a Power Rule
Quotient to a Power Rule for Exponents

a
b
n
n
a
 n
b
if b  0.
Example: Simplify each expression:
10
x
x 
10
 y
y
 
10
a.)
b.)
3 4
 3a  
 2 
 b 
3 a
4

3 4
b 
2 4
12
81
a
 8
b
Zero Exponent
If a is a nonzero real number (that is, a  0), we define
a0 = 1
Example: Simplify each expression.
a.)
b.)
(24ab)0  1
3 0
 3a
 2  1
 b 
Negative Exponent
If n is a positive integer and if a is a nonzero real number (that is, a  0),
then we define
a  n  1n
a
Example: Simplify each expression.
a.)
(4) 2 
1  1
(4)2 16
b.)
(ab) 3 
1  1
(ab)3 a 3b3
Negative Exponent
If a and b are real numbers and n is an integer, then
 
a
b
n
n
 b
a
if a  0, b  0
Example: Simplify each expression.
a.)

3
x
2
5
b.)

 x
3
2
5
2
x

9
5 5
xy
x
y


 ab  
 xy   ab   a5b5
 
Simplifying Expressions
How to Simplify Expressions Using the Product Rule and
the Negative Exponent Rule
Step 1: Rearrange the factors.
Step 2: Find each product.
Step 3: Simplify. Write the product so that the exponents are positive.
Example: Simplify the expression:







2a3b4 6a 2b


2a3b4 6a 2b   2(6)  a3  a 2 b4  b Rearrange factors.
 12a1b3
 12a
b3
Find each product.
Simplify.
Simplifying Expressions
How to Simplify Expressions Using the Quotient Rule and
the Negative Exponent Rule
Step 1: Write the quotient as the product of factors.
Step 2: Find each quotient.
Step 3: Simplify. Write the quotient so that the exponents are positive.
Example: Simplify the expression:
12 x 2 y 5 12 x 2 y 5
  4
4
8 x y
8x y
 3  x 2 y 4
2
3y4
 2
2x
12 x 2 y 5
8x4 y
Write the quotient as products.
Find each quotient.
Simplify.
Simplifying Expressions
How to Simplify Expressions Using the Power Rule and
the Negative Exponent Rule
Step 1: Write the quotient as the product of factors.
Step 2: Find each product.
Step 3: Simplify. Write the product so that the exponents are positive.
 20a 3b5 
Example: Simplify the expression: 

 4a 6b 
2
2
 20a b    20  a 3  b5 


  4
6
6
b
a


4
a
b


2
4


  5b9 
 a 
2
18
 a9 
a
 4  
25b8
 5b 
3 5
2
Write the quotient as products.
Find each product.
Simplify.
Summary - Laws of Exponents
1. x  x  x
m
 
3. x
m n
m
n
mn
2. xy  x y
m
m
x
mn
x
mn
5. n  x
x
m
x
x
4.    m
y
 y
m
m
Other Properties of Exponents
1
x 
x
x 1
1
0
Any single number or variable is always
to the first power
33
1
aa
1
2 x  2 x  2 x 
1 1
1
Your Turn:
x x  x
2
x 
4 3
3
x
43
2 3
x
x
xy
5
12
3
 x y
3
3
Your Turn:
3
x
x
   3
y
y
 
7
74
x
x
3


x
4
x
1
5
1
1
x


2
7 5
7
x
x
x
3
Your Turn:
2a 3  7 a 4  2  7a 34  14a 7
 5r 2  8r 3  2r 2   5  8  2r 23 2   80r 7
2m n 
2 5 3
3xy
3
13
23 53
2 m n
 2 m n  8m n
3
 3 x y  27 x y
3
3
3
3
6 15
6 15
3
2
2 2
2
2
a
2
a
4
a
 
   2 2  2
9b
 3b  3 b
8 x 4 8 x 41

 4x 3
2x 2 1
9z3 9 1  3 1  3
2
2

53
5
x
x
3z
3z
Your Turn:
3x 3 y 2 z  7 xyz2  3  7x31 y 21 z1 2  21x 4 y 3 z 3


 8xy2  3xy   2 xy3   8  3  2x111 y 213  48x 3 y 6
3x y  2 xy 
2
3 2
2 2
 312 x 22 y 32 212 x12 y 22  
9 x 4 y 6  4 x 2 y 4  9  4x 4 2 y 6 4  36 x 6 y10
3
 5a b 
513 a 33b13 53 a 9b 3 125a 9b 3 125a 93 125a 6

  13 13 23  3 3 6 


6 3
3 6
3
2 
3
a
b
27
b
3
a
b
27
a
b
27
b
3
ab


3
Transformations Involving
Exponential Functions
Transformation
Equation
Description
Horizontal translation
g(x) = bx-c
• Shifts the graph of f (x) = bx to the left c units if c < 0.
• Shifts the graph of f (x) = bx to the right c units if c > 0.
Vertical stretching or
shrinking
g(x) = c bx
Multiplying y-coordintates of f (x) = bx by c,
• Stretches the graph of f (x) = bx if c > 1.
• Shrinks the graph of f (x) = bx if 0 < c < 1.
Reflecting
g(x) = -bx
g(x) = b-x
• Reflects the graph of f (x) = bx about the x-axis.
• Reflects the graph of f (x) = bx about the y-axis.
Vertical translation
g(x) = bx + c
• Shifts the graph of f (x) = bx upward c units if c > 0.
• Shifts the graph of f (x) = bx downward c units if c < 0.
Example
Use the graph of f (x) = 3x to obtain the graph of g(x) = 3 x+1.
Solution Note that the function g(x) = 3x+1 has the general form g(x) = bx-c,
where c = 1. Because c < 0, we graph g(x) = 3 x+1 by shifting the graph of f
(x) = 3x one unit to the left.
g(x) = 3x+1
(-1, 1)
-5 -4 -3 -2 -1
f (x) = 3x
(0, 1)
1 2 3 4 5 6
Transforming Exponential
Functions
• Describe how to transform the graph of f(x)=2x
into the graph of g(x).
g ( x)  2
x 1
Solution: Transformation of
x
2 to 2
x1
Transforming Exponential
Functions
• Describe how to transform the graph of f(x)=2x
into the graph of h(x).
h( x )  2
x
Solution: Transformation of
x
2 to 2
x
Reflected about y-axis
y2
x
This equation could be rewritten in a different
form:
y2
x
1 1
 x  
2
2
x
So if the base of our exponential function is
between 0 and 1 (which will be a fraction),
the graph will be decreasing. It will have the
same domain, range, intercepts, and
asymptote.
Two ways to write a decay function;
1. Base is a fraction
2. Negative exponent
State “exponential growth” or “exponential decay”
a.) y = e2x
k > 0, exponential growth
c.) y = 2–x
b>1 so growth,
but reflect over y-axis, so decay
b.) y = e–2x
k < 0, exponential decay
d.) y = 0.6–x
0<b<1 so decay,
but reflect over y-axis, so growth
Transforming Exponential
Functions
• Describe how to transform the graph of f(x)=2x
into the graph of k(x).
k ( x)  3  2
x
Solution: Transformation of
2 to 3  2
x
x
y2
All of the transformations that you learned apply to all
functions, so what would the graph of
look like?
x
x
y  2 3
up 3
right 2
up 1
Reflected over x
axis
y  1 2
x
down 1
y2
x2
1
Your Turn:
Sketch a graph using transformation of the following:
1.
f ( x)  2 x  3
2.
f ( x)  2 x  1
3.
f ( x)  4
x 1
1
The order of transformations: horizontal, reflection (horz., vert.),
vertical.
Transformation of
Exponential Function
• What are the effects of a, c and d in the transformation of
the exponential function
• Example:
y  a b
xc
y  2  3
d
x4
5
Transformation:
y  2  3
x4
5
y 3
y  2  3x 4  5
x
Transformations
• Exponential graphs, like other functions we have studied, can be dilated,
reflected and translated.
• It is important to maintain the same base as you analyze the transformations.
g ( x)  2  3
x
Vertical shift up 3
g ( x )  3(2 x )  1
Reflect @ x-axis
Vertical stretch 3
Vertical shift down 1
Your Turn:
y  (2)
x 1
1
Horizontal shift right 1.
Reflect about the x-axis.
y  (3)
1
2
x2
3
Horizontal shift left 2.
Vertical shrink ½ .
Vertical shift up 1.
Vertical shift down 3.
Summary of Transformations
f(x) =
Reflection over
the x-axis
Vertical Stretch
by factor of a
±x-c
±a·b +d
Base
Horizontal translation
by of c units(opposite
direction of sign)
Reflection over
the y-axis
(neg. x makes
decay curve out
of growth curve)
Vertical translation
by of d units(same
direction of sign)
y = d equation of
horizontal asymptote
The Natural Base e
An irrational number, symbolized by the letter e, appears as the base in
many applied exponential functions. This irrational number is approximately
equal to 2.72.
The number e is called the natural base. The function f (x) = ex is called the
e
natural exponential function.2.71828...
f (x) = 3x
f (x) = ex
4
f (x) = 2x
(1, 3)
3
(1, e)
2
(1, 2)
(0, 1)
-1
1
The Natural Base e
• Represented by e to honor
Euler who discovered the
number.
e  2.718......
Transforming Exponential Functions
Your Turn:
f ( x)  3e x  2
f  x   e x  1
Vertical stretch 3.
Reflect @ x-axis.
Vertical shift up 2.
Vertical shift down 1.
f  x   ex2  2
Horizontal shift left 2.
Vertical shift up 2
Assignment
• Pg. 193 – 195; 5 – 16 all, 17 – 21 odd