* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download Set #6 - McMaster Physics and Astronomy
Fictitious force wikipedia , lookup
Newton's laws of motion wikipedia , lookup
Classical central-force problem wikipedia , lookup
Rotating locomotion in living systems wikipedia , lookup
Continuously variable transmission wikipedia , lookup
Jerk (physics) wikipedia , lookup
Modified Newtonian dynamics wikipedia , lookup
Seismometer wikipedia , lookup
Relativistic mechanics wikipedia , lookup
Hunting oscillation wikipedia , lookup
Center of mass wikipedia , lookup
Moment of inertia wikipedia , lookup
Centripetal force wikipedia , lookup
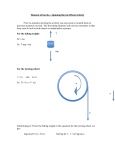
Practice Problems 6 1. Four masses are connected by 12.5 cm long, massless, rigid rods. If mA=110.0 g, mB=241.0 g, mC=205.0 g, and mD=211.0 g, what are the coordinates of the center of mass if the origin is located at mass A? Answer: 6.78e-02 m 7.27e-02 m (x coordinate first followed by the y coordinate.) 2.What is the moment of inertia about a diagonal axis that passes through masses B and D. Answer: 2.46e-03 kg*m^2 3. An object's moment of inertia is 2.29 kg·m2. Its angular velocity is increasing at the rate of 5.06 rad/s per second. What is the torque on the object? Answer: 1.16e+01 N*m 4. A 3.15 kg ball and a 6.30 kg ball are connected by a 1.31 m long rigid, massless rod. The rod is rotating clockwise about its center of mass at 24.2 rpm. What torque will bring the balls to a halt in 6.97 s? Answer: 1.31e+00 N*m 5. A potter's wheel—a thick stone disk with a radius of 0.450 m and a mass of 128 kg—is freely rotating at 52.0 rev/min. The potter can stop the wheel in 5.95 s by pressing a wet rag against the rim and exerting a radially inward force of 82.0 N. Calculate the effective coefficient of kinetic friction between the wheel and the rag. Answer: 3.21E-01 6. A cylindrical fishing reel has a moment of inertia of I=6.50×10-4 kg·m2 and a radius of 3.88 cm. A friction clutch in the reel exerts a restraining torque of 1.19 N·m if a fish pulls on the line. The fisherman gets a bite, and the reel begins to spin with an angular acceleration of 67.1 rad/s2. What is the force of the fish on the line? Answer: 3.18e+01 N 7. How much line unwinds in 0.460 s? Answer: 2.75e-01 m 8. A cable passes over a pulley. Because of friction, the tension in the cable is not the same on opposite sides of the pulley. The force on one side is 135 N, and the force on the other side is 106 N. Assuming that the pulley is a uniform disk of mass 2.36 kg and radius 0.820 m, determine its angular acceleration. Answer: 3.00e+01 rad/s^2 9. An m = 14.7 kg mass is attached to a cord that is wrapped around a wheel of radius r = 11.6 cm (see the figure below). The acceleration of the mass down the frictionless incline is measured to be a = 2.02 m/s2. Assuming the axle of the wheel to be frictionless, and the angle to be θ = 35.3° determine the tension in the rope. Answer: 5.36e+01 N 10. Determine the moment of inertia of the wheel. Answer: 3.57e-01 kg*m^2 11. Determine angular speed of the wheel 1.85 s after it begins rotating, starting from rest. Answer: 3.22e+01 rad/s 12. A m2 = 4.63 kg mass is connected by a light cord to a m1 = 2.10 kg mass on a smooth surface (see the figure below). The pulley rotates about a frictionless axle and has a moment of inertia of 0.513 kg·m2 and a radius of 0.257 m. Assuming that the cord does not slip on the pulley, find the acceleration of m1. Answer: 3.13e+00 m/s^2 13. Find the tension T1. Answer: 3.09e+01 N 14. Find the tension T2. Answer: 6.58e+00 N 15. When the motor in the figure below raises the m = 1050 kg mass, it produces a tension of 1.26×104 N in the cable on the right side of the pulley. The pulley has a moment of inertia of 73.2 kg·m2 and a radius of 0.800 m. The cable rides over the pulley without slipping. Determine the acceleration of the m = 1050 kg mass. Use g=9.81 m/s2. Answer: 1.97e+00 m/s^2