Download CENTRAL LIMIT THEOREM

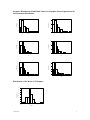
CENTRAL LIMIT THEOREM
The Central Limit Theorem is important because it allows us to develop a process to
estimate and test the mean of a population using a sample.
The Central Limit Theorem:
 specifies a theoretical distribution
 the distribution is formulated by the selection of all possible random samples of a
fixed size n
 a sample mean is calculated for each sample producing a sampling distribution
SAMPLING DISTRIBUTION OF THE MEAN
The sampling distribution of the mean is formed by taking the mean of samples from a
given population
 The mean of the sample means is equal to the mean of the population from which the
samples were drawn.
 The standard deviation of the distribution is  divided by the square root of n. (it is
called the standard error.)
STANDARD ERROR
Standard Deviation for the Distribution of Sample Means
x 

n
CENTRAL LIMIT THEOREM
1. Consider a population with mean  and standard deviation .
2. Draw a random sample of n observations from this population where n is a large
number (n> 30).
3. Find the mean x for each and every sample.
4. The distribution of the sample means x will be approximately normal. This
distribution is called the Sampling Distribution of the Means or the Distribution of
Sample Means.
5. The mean and standard deviation (called the standard error) of the Distribution of
Sample Means is:
x  
The mean of the Sampling Distribution equals the mean of the Population

The standard error equals the standard deviation of the population divided
by the square root of the sample size.
x 
6.
n
The approximation becomes more accurate as n becomes large.
3360clt.doc
1
Example: Distribution of Individual Values for 6 Samples from a Population with
an Exponential Distribution
30
Frequency
Frequency
30
20
10
0
20
10
0
0.0
0.5
1.0
1.5
2.0
2.5
3.0
3.5
4.0
4.5
5.0
0.0
0.5
1.0
1.5
2.0
C25
2.5
3.0
3.5
4.0
4.5
5.0
C12
35
30
30
Frequency
Frequency
25
20
15
10
20
10
5
0
0
0
1
2
3
4
5
6
0
1
2
C1
3
4
5
6
C10
35
40
30
30
Frequency
Frequency
25
20
15
10
20
10
5
0
0
0
1
2
3
4
5
6
0
C1
1
2
3
4
5
6
C30
Distribution of the Means of 30 Samples
35
30
Frequency
25
20
15
10
5
0
0.5
1.0
1.5
C31
3360clt.doc
2
EXAMPLE
A certain brand of tires has a mean life of 25,000 miles with a standard deviation of 1600
miles. What is the probability that the mean life of 64 tires is less than 24,600 miles?
Solution
The sampling distribution of the means has a mean of 25,000 miles (the population mean)
 = 25000 mi.
and a standard deviation (i.e. standard error) of
 x = 1600/8 = 200
Convert 24,600 mi. to a z-score and use the normal table (or Excel) to determine the
required probability.
z = (24600-25000)/200 = -2
P(z< -2) = 0.0228
or 2.28% of the sample means will be less than 24,600 mi.
3360clt.doc
3