* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download CENTRAL LIMIT THEOREM
Survey
Document related concepts
Transcript
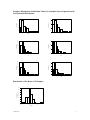
CENTRAL LIMIT THEOREM The Central Limit Theorem is important because it allows us to develop a process to estimate and test the mean of a population using a sample. The Central Limit Theorem: specifies a theoretical distribution the distribution is formulated by the selection of all possible random samples of a fixed size n a sample mean is calculated for each sample producing a sampling distribution SAMPLING DISTRIBUTION OF THE MEAN The sampling distribution of the mean is formed by taking the mean of samples from a given population The mean of the sample means is equal to the mean of the population from which the samples were drawn. The standard deviation of the distribution is divided by the square root of n. (it is called the standard error.) STANDARD ERROR Standard Deviation for the Distribution of Sample Means x n CENTRAL LIMIT THEOREM 1. Consider a population with mean and standard deviation . 2. Draw a random sample of n observations from this population where n is a large number (n> 30). 3. Find the mean x for each and every sample. 4. The distribution of the sample means x will be approximately normal. This distribution is called the Sampling Distribution of the Means or the Distribution of Sample Means. 5. The mean and standard deviation (called the standard error) of the Distribution of Sample Means is: x The mean of the Sampling Distribution equals the mean of the Population The standard error equals the standard deviation of the population divided by the square root of the sample size. x 6. n The approximation becomes more accurate as n becomes large. 3360clt.doc 1 Example: Distribution of Individual Values for 6 Samples from a Population with an Exponential Distribution 30 Frequency Frequency 30 20 10 0 20 10 0 0.0 0.5 1.0 1.5 2.0 2.5 3.0 3.5 4.0 4.5 5.0 0.0 0.5 1.0 1.5 2.0 C25 2.5 3.0 3.5 4.0 4.5 5.0 C12 35 30 30 Frequency Frequency 25 20 15 10 20 10 5 0 0 0 1 2 3 4 5 6 0 1 2 C1 3 4 5 6 C10 35 40 30 30 Frequency Frequency 25 20 15 10 20 10 5 0 0 0 1 2 3 4 5 6 0 C1 1 2 3 4 5 6 C30 Distribution of the Means of 30 Samples 35 30 Frequency 25 20 15 10 5 0 0.5 1.0 1.5 C31 3360clt.doc 2 EXAMPLE A certain brand of tires has a mean life of 25,000 miles with a standard deviation of 1600 miles. What is the probability that the mean life of 64 tires is less than 24,600 miles? Solution The sampling distribution of the means has a mean of 25,000 miles (the population mean) = 25000 mi. and a standard deviation (i.e. standard error) of x = 1600/8 = 200 Convert 24,600 mi. to a z-score and use the normal table (or Excel) to determine the required probability. z = (24600-25000)/200 = -2 P(z< -2) = 0.0228 or 2.28% of the sample means will be less than 24,600 mi. 3360clt.doc 3




![z[i]=mean(sample(c(0:9),10,replace=T))](http://s1.studyres.com/store/data/008530004_1-3344053a8298b21c308045f6d361efc1-150x150.png)








