Download Electricity & Magnetism Review 4: Units 17-19, 22-23

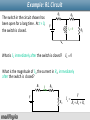
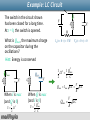
Electricity & Magnetism
Review 4: Units 17-19, 22-23
17. Faraday’s Law
18. Induction and RL Circuits
19. LC circuits
22. Maxwell’s Displacement current and EM waves
23. Properties of EM waves
Mechanics Review 2 , Slide 1
Review Formulas
Faraday’s Law e = - dFB
 
 B   B  dA
dt
Energy Density
1 2
e0 2
uB =
B uE = E
2
2m 0
Maxwell’s Equations
Poynting vector
EM Intensity I = S = cu
avg
avg
Self-Inductance e L = -L
L=
FB
I
1
U L = LI 2
2
dI
dt
R-L circuit I = e (1- e-Rt L )
R
(charging)
R-C circuit I = dQ = -wQmax sin(wt + f )
dt
w=
1
LC
Emax = cBmax
Radiation Pressure
P = I/c
Example: Faraday’s Law
The current through the long straight wire is given by
I(t) = Imax sinωt.
Calculate the magnetic flux through the loop and the current I2
induced in the rectangular loop, which has total resistance R.
0 I (t )
B( r , t ) 
2 r
dFB
e =dt
I2 

R
Example: EM wave
The magnetic field of a plane EM wave is (z is in meters and t is
in seconds):
z 107 t
6
B  1.2  10 sin(
240

8
)T
Find:
(a) f, T, λ.
(b) Emax.
(c) The average power per square meter carried by the wave.
(d) The force exerted on a surface perpendicular to the wave
that reflects 80% of the incident radiation and has area 5.0 m2.
k=2π/λ ω = 2π/T = 2πf
 1 dU
| S |
A dt
Emax = cBmax
I = Savg
P = (I/c) ×1.8
F = PA
Example: Rotating Loop
Assume a loop with N turns, all of
the same area A rotating in a
magnetic field B.
Calculate the induced emf in the
coil.
The flux through the loop at any
time t is:
B = NBA cos q = NBA cos wt
dFB
e = -N
dt
= NABw sin w t
Example: Induced Electric Field
A long solenoid of radius R has n
turns of wire per unit length and
carries a current I = Imaxcosωt.
Determine the magnitude of the
induced electric field outside the
solenoid at a distance r > R from its
long central axis.
Use Ampere’s Law to find B
B = m0 nI
B = BA = BπR2
Example: Solenoid
A solenoid of N turns, length z and radius r, curries current I.
What is the magnetic field in the solenoid?
What is the total magnetic flux through the solenoid?
What is the inductance of the solenoid?
How much magnetic energy is stored in the solenoid?
Use Ampere’s Law to find B
B = m0 NI / z
B = B(NA) = Nπr2
L = FB / I = B(N p r 2 ) / I
L = m0 N 2p r 2 / z
L
1 2
U L = LI
2
Example: LC circuit
In the LC circuit below switch A is closed for a long time. It is
then opened and switch B is closed at t = 0. Given ε, C and L.
Find:
ω 1
(a) The frequency and period of the oscillation.
LC
(b) The charge Q(t) on the capacitor.
(c) The current I(t) in the inductance.
Qmax = Ce
Q(t) = Qmax cos(wt)
I(t) =
dQ
= -wQmax sin(wt)
dt
Example: RL Circuit
The switch in the circuit shown has
been open for a long time. At t = 0,
the switch is closed.
R1
R2
V
L
What is IL immediately after the switch is closed?
IL  0
R3
IL  0
What is the magnitude of I2, the current in R2, immediately
after the switch is closed?
R1
I
R2
V
R3
V
I2 
R1  R2  R3
Example: RL Circuit
R1
The switch in the circuit shown
has been open for a long time.
At t  0, the switch is closed.
What is the magnitude of VL
immediately after the switch is
closed?
I2
V
L
IL(t  0)  0
V
( R2  R3 )
R1  R2  R3
R3
I2(t  0)  V/(R1 R2 R3)
VL(t  0)  V(R2 R3)/(R1 R2 R3)
Kirchhoff’s Rule: I2 R2  I2 R3 VL  0
VL 
R2
VL  I2 (R2  R3)
Example: RL Circuit
The switch in the circuit shown has
been closed for a long time.
R1
R2
V
L
R3
What is I2, the current through R2 ?
(Positive values indicate current flows to
the right)
After a long time, dI/dt  0 and the voltage VL  0
Then the voltage across R2  R3 is 0 so the current through R2  R3 must be
zero! I 2  0
Now the switch is opened. What is I2,
R1
the current through R2 immediately
R2 I2
after switch is opened ?
V
INDUCTORS: Current cannot change
L
R3
discontinuously!
IL  V/R1
I2  V/R1
Example: RL Circuit
The switch in the circuit shown has
been closed for a long time. Now the
switch is opened.
R1
V
L
What is I2, the current through R2 as
a function of time?
Kirchhoff’s Rule: I2 R2  I2 R3  VL  0
dI 2
L
+ I 2 (R2 + R3 ) = 0
dt
V
I 2 (t) = I 2 (0)e-t/t = e-t/t
R1
L
t=
R2 + R3
R2
R3
R1
R2
V
L
R3
R2
L
R3
I2
Example: LC Circuit
The switch in the circuit shown
has been closed for a long time.
At t  0, the switch is opened.
IL
V
C
L
R
What is QMAX, the maximum
charge on the capacitor?
Once switch is opened, we have an LC circuit.
What is IL, the current in the inductor,
immediately after the switch is opened?
Take positive direction as shown.
Current through inductor is continuous.
IL
V
IL
L
IL
VL  0
C
R
IL > 0
V
I L (0) =
R
before switch is opened: all current goes through inductor in direction shown
Example: LC Circuit
The switch in the circuit shown
has been closed for a long time.
At t = 0, the switch is opened.
IL
V
L
VC  0
R
IL (t  0 ) > 0
What is the energy stored in the capacitor immediately after the
switch is opened?
before switch is opened:
dIL/dt ~ 0  VL  0
BUT: VL  VC
since they are in parallel
VC  0
after switch is opened:
VC cannot change abruptly
VC  0
UC  ½ CVC2  0 !
C
Example: LC Circuit
The switch in the circuit shown
has been closed for a long time.
At t = 0, the switch is opened.
What is Qmax, the maximum charge
on the capacitor during the
oscillations?
Hint: Energy is conserved
Imax
Qmax
C
L
C
L
IL
V
R
IL (t  0 )  V/R
1
U  LI 2
2
When Q is max
(and I is20)
U
1 Qmax
2 C
VC (t  0 )  0
2
1 2 1 Qmax
LI 
2
2 C
Qmax  I max
When I is max
(and Q is 0)
C
L
Qmax 
V
LC 
LC
R
V
LC
R
Example: LC Circuit
The switch in the circuit shown
has been closed for a long time.
At t = 0, the switch is opened.
What is IL(t), the current through
the inductor as a function of time,
in the direction shown?
Q(t) = Qmax cos(wt + f )
w
Qmax
1
LC
V

LC
R
IL
V
C
L
R
IL (t  0 )  V/R
VC (t  0 )  0
To find the phase constant ϕ look at
the initial conditions:
p
Q(0) = Qmax cos(f ) = 0 ® f = ±
2
V
p
I(0) = -wQmax sin(f ) = ® f = R
I L (t) =
V
cos(w t)
R
2
Example: EM Wave
Estimate the maximum magnitudes of the electric and
magnetic fields of the light that is incident on a page
because of the visible light coming from your desk
lamp. Treat the 60 W light bulb as a point source of EM
radiation that is 5% efficient in transforming electrical
energy into visible radiation.
2
Emax
I=
2m 0 c
Emax = cBmax
Example: Toroid
The toroid consists of N turns and has a rectangular cross
section. Its inner and outer radii are a and b. Find:
(a) The magnetic field inside the toroid at a distance r from the
center.
(b) The total magnetic flux through the toroid if the current is I.
(c) The inductance of the toroid.
(d) The magnetic energy stored in the toroid.
I enc
mo NI
= NI B =
2p r
 
 B   B  dA
NFB
L=
I
1 2
U L = LI
2