* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Document
Survey
Document related concepts
Transcript
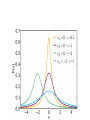
The Formation of Spectral Lines I. Line Absorption Coefficient II. Line Transfer Equation Line Absorption Coefficient Main processes 1. Natural Atomic Absorption 2. Pressure Broadening 3. Thermal Doppler Broadening Line Absorption Coefficient The classical model of the interaction of light with a photon is a plane electromagnetic wave interacting with a dipole. 2 E ∂ ∂2 E 2 = v ∂ x2 ∂ t2 Treat only one frequency since by Fourier composition the total field is a sum of all sine waves. E = E0 e–iw(x/v – t) The wave velocity through a medium ½ e m 0 0 v=c ( e m e and m are the electric and magnetic permemability in the medium and free space. For gases m = m0 ( Line Absorption Coefficient The total electric field is the sum of the electric field E and the field of the separated charges induced by the electric field which is 4pNqz where z is the separation of the charges and N the number of dipoles per unit volume The ratio of e/e0 is just the ratio of the field in the medium to the field in free space E + 4pNqz e = e0 E We need z/E = 1+ 4pNqz E Line Absorption Coefficient For a damped harmonic oscillator where z is the induced separation between the dipole charges d2 z d t2 dz + g dt + w0 2 e E0 eiwt = m e,m are charge and mass of electron g is damping constant Solution: z = z0e–iwt E0 eiwt e z= m w20 – w2 + igw E e = m w20 – w2 + igw Line Absorption Coefficient 2 e 4pNe 1+ = e0 E 1 w02 – w2 + igw For a gas e ≈ e0 so second term is small compared to unity The wave velocity can now be written as 2 1 4pNe e ½ (e ≈ 1 + 2 m 0 ( c ≈ v 1 w02 – w2 + igw ½ Where we have performed a Taylor expansion (1 + x) = 1 + ½ x for small x Line Absorption Coefficient c ≈ 1+ v 2pNe2 m w20 – w2 (w20 – w2)2 + g2w2 –i gw (w20 – w2)2 + g2w2 This can be written as a complex refractive index c/v = n – ik. When it is combined with iwx/v it produces an exponential extinction e–kwx/c . Recall that the intensity is EE* where E* is the complex conjugate. The light extinction can be expressed as: I = I0 e–kwx/c = I0e–lnrx Line Absorption Coefficient ln r = 4pNe2 gw mc (w20 – w2)2 + g2w2 This function is sharply peaked giving non-zero values when w ≈ w0 2 2 w0 – w =(w0 – w)(w0 + w) ≈ (w0 – w)2w ≈ 2wDw The basic form of the line absorption coefficient: ln r = Npe2 gw mc Dw2 + (g/2)2 This is a damping profile or Lorentzian profile, a Cauchy curve, or the „Witch of Agnesi“ Line Absorption Coefficient Consider the absorption coefficient per atom, a, where lnr = Na 2pe a= mc gw Dw2 + (g/2)2 g/4p 2pe a= mc Dn2 + (g/4p)2 2pe a= mc l2 c gl2/4pc Dl2 + (gl2/4pc)2 Line Absorption Coefficient ∞ ∫ a dn = 0 pe2 mc This is energy per unit atom per square radian that the line absorbs from In A quantum mechanical treatment ∞ ∫0 a dn = f pe2 mc f is the oscillator strength and is related to the transition probability Blu ∞ ∫0 a dn = Blu hn Line Absorption Coefficient f= mc pe2 Blu hn = 7.484 × 10–7 Blu l gu A ul f= 2pe2n2 gl mc 3 There is also an f value for emission gu fem = gl fabs Most f values are determined from laboratory measurements and most tables list gf values. Often the gf values are not well known. Changing the gf value changes the line strength, which is like changing the abundance. Standard procedure is you take a gf value for a line, fit it to the solar spectrum, and change gf until you match the solar line. This value is then good for other stars. The Damping Constant for Natural Broadening Classical dipole emission theory gives an equation of the form dW 2 e2 w2 –g W – = = W 3 dt 3 mc Solution of the form W= W0e–gt 2 w2 2e 2 in cm g = = 0.22/l 3 3mc The quantum mechanical radiation damping is an order of magnitude larger which is consistent with observations. However, the observed widths of spectral lines are dominated by other broadening mechanisms Pressure Broadening Pressure broadening involves an interaction between the atoms absorbing the light and other particles (electrons, ions, atoms). The atomic levels of the transition of interest are perturbed and the energy altered. • Distortion is a function of separation R, between absorber and perturber • Upper level is more strongly altered than the lower level u hn E l 1 2 3 R 1: unperturbed energy 2. Perturbed energy less than unperturbed 3. Energy greater than unperturbed Pressure Broadening Energy change as a function of R: DW = Const/Rn n Type Lines affected Perturber 2 Linear Stark Hydrogen Protons, electrons 4 Quadratic Stark Most lines, especially in hot stars Ions, electrons 6 Van der Waals Most lines, especially in cool stars Neutral hydrogen Dn = Cn /Rn Pressure Broadening: The Impact Approximation Duration of encounter typically 10–9 secs Dtj First formulated by Lorentz in 1906 who assumed that the electromagnetic wave was terminated by the impact and with the remaining photon energy converted to kinetic energy Photon of duration Dt is an infinite sine wave times a box Spectrum is just the Fourier transform of box times sine which is sinc pDt(n-n0) and indensity is sinc2pDt(n-n0). Characteristic width is Dn= 1/Dt Pressure Broadening: The Impact Approximation With collisions, the original box is cut into many shorter boxes of length Dtj < Dt The distribution, P, of Dtj is:. dP(Dtj) = e–Dtj/Dt0 dDtj/Dt0 Because Dtj < Dt the line is broadened with Dnj = 1/Dtj. The Fourier transform of the sum is the sum of the transforms. t0 is an average length of an uninterrupted time segment The line absorption coefficient is the weighted average: 2 ∞ ∫ Dt2 0 a= a= C sinpDt(n – n0) pDt(n – n0) e–Dt/Dt0 dDt Dt0 C 4p2(n – n0)2 + (1/Dt0)2 gn/4p (n – n0)2 + (gn/4p)2 In other words this is the Lorentzian. To use this in a line profile calculation need to evaluate gn = 2/Dt0. This is a function of depth in the stellar atmosphere. Evaluation of gn Simplest approach is to assume that all encounters are in one of two groups depending on the strength of the encounter. If phase shift is too small ignore it. The cumulative effect of the change in frequency is the phase shift. f = 2p ∫ ∞ ∞ ∫ Dn dt = 2p Cn 0 Dn = Cn /Rn R–n dt 0 v y Assume perturber moves past atom in a straight line r = R cos q ∞ ∫ f = 2p Cn cosnq dtn r 0 Atom r q x R Perturber Evaluation of gn v = dy/dt = (r/cos2q) dq/dt => dt = (r/v)dq/cos2q p/2 n–2 q dq n f = 2p C cos vrn–1 ∫ –p/2 Usually define a limiting impact parameter for a significant phase shift f = 1 rad p/2 r0 = 2p Cn v ∫ n p/2 ∫ cosn–2 q dq –p/2 2 p 3 2 4 p/2 6 3p/8 1/(n–1) cosn–2 q dq –p/2 r0 is an average impact parameter and we count only those with r < r0 Evaluation of gn The number of collisions is pr20vNT where N is the number of perturbers per unit volume, T is the interval of the collisions. If we set T = Dt0, the average length of an uninterupted segment a photon will travel. Over this length the number of collisions should be ≈ 1. pr02 vNDt0 ≈ 1 gn = 2/Dt0 = 2pr02vN Evaluation of gn : Quadratic Stark In real life you do not have to calculate gn For quadratic Stark effect (perturbations by charged particles) g4 = 39v⅓C4⅔N Values of the constant C4 has been measured only for a few lines Na 5890 Å log C4 = –15.17 Mg 5172 Å log C4 = –14.52 Mg 5552 Å log C4 = –13.12 Evaluation of gn For van der Waals (n=6) you only have to consider neutral hydrogen and helium log g6 ≈ 19.6 + 0.4 log C6(H) + log Pg – 0.7 log T log C6 = –31.7 Linear Stark in Hydrogen Struve (1929) was the first to note that the great widths of hydrogen lines in early type stars are due to the linear Stark effect. This is induced by ions near the hydrogen atom. Above are the Balmer profiles for an A0 V star. Thermal Broadening Thermal motion results in a component of the thermal motion along the line of sight Dl Dn = l n = vr vr = radial velocity c N We can use the Maxwell Boltzmann distribution [( 2 [( vr dN 1 = exp – v v 0 p½ 0 N dvr 1.18s variance v02 = 2kT/m v Velocity Thermal Broadening The Doppler wavelength shift Dl exp – DlD [( [( 2 ( 2kT ½ m Dl d Dl D ( dN = p–½ N ( ( v0 n DnD = n = c c 2kT ½ m ( DlD = l l = c c v0 ( The energy removed from the intensity is (pe2f/mc)(l2/c) times dN/N l2 f c 1 exp – DlD [( Dl DlD 2 [( a dl = p½e2 mc dl The Combined Absorption Coefficient The Combined absorption coefficient is a convolution of all processes a(total) = a(natural)*a(Stark)*a(v.d.Waals)*a(thermal) The first three are easy as they can be defined as a single dispersion profile with g: g= gnatural + g4 + g6 The last term is a Gaussian so we are left with the convolution of a Gaussian with the Dispersion (Lorentzian) profile: g/4p pe2 f a= mc Dn2 + (g/4p)2 * 2 Lorentzian 1 p½ e–(Dn/DnD) Gaussian 2 The convolution is the Voigt Function The Combined Absorption Coefficient p½e2 f H(u,a) a= mc DnD H(u,a) is the Hjerting function u = Dn/DnD = Dl/DlD H(u,a) = ∫ –∞ ∞ g a= 4p 1 DnD = g 4p 2 l0 c 1 DlD g/4p2 –(Dn1/DnD)2 2 2 e dn1 (Dn – Dn1) + (g/4p) a H(u,a) = p ∫ –∞ ∞ 2 e– du u (u – u11)2 + a2 1 The absorption coefficient can be calculated using the series expansion: H(u,a) = H0(u) + aH1(u) + a2H2(u) + a3H3(u) + a4H4(u) + Hjerting function tabulated in Gray The Line Transfer Equation dtn = (ln + kn)rdx ln= line absorption coefficient kn= continuum absorption coefficient Source function: Sn = jln + jcn l n + kn jln = line emission coefficient jcn = continuum emission coefficient dIn = –In + Sn dtn This now includes spectral lines Using the Eddington approximation S(t) = 3Fn (t + ⅔) 4p At tn = (4p – 2)/3 = t1 , Sn(t1) = Fn(0), the surface flux and source function are equal Across a stellar line ln changes being larger towards the center of the line. This means at line center the optical depth is larger, thus we see higher up in the atmosphere. As one goes farther from line center, ln decreases and the condition that tn = t1 is deeper in the atmosphere. An absorption line is formed because the source function decreases outward. Computing the Line Profile In local thermodynamic equilibrium the source function is the Planck function ∞ ∫ F = 2p Bn(T) E2(tn)dtn 0 ∞ dtn = 2p Bn(tn) E2(tn) dt dt0 0 ∫ 0 ∞ dlog t0 l n + kn = 2p Bn(tn) E2(tn) t0 k0 log e ∫ –∞ Computing the Line Profile To compute tn log t0 tn(t0) = ∫ –∞ Fc – Fn Fc ln + kn dlog t0 k0 t0 log e Optical depth without ln Optical depth with ln Sn(tc=t1) – Sn(tn = t1) = Sn(tc=t1) Take the optical depth and divide it into two parts, continuum and line t0 t0 tn = ∫ ln dt + k0 0 0 tn = tl + tc ∫ kn dt k0 0 0 t0 Computing the Line Profile t l ≈ l n t0 k0 tc ≈ k n t 0 k0 Ignoring the change with depth We need Sn(tn = t1) = Sn(tl + tc = t1) = Sn(tc = t1 – tl) We are considering only weak lines so tl << tc and evaluate Sn at t1 – tl using a Taylor expansion around tc = t1 Sn(tn = t1) ≈ Sn(tc = tn) + dSn (–t ) l dtn Computing the Line Profile Fc – Fn Fc = tl Sn(tc=t1) dlnSn t = l dt c dSn dtc t1 ln t dlnSn ≈ k c dt c n t1 ln = C k n Weak lines • Mimic shape of ln i.e. a Voigt profile • Strength of spectral line can be increased either by decreasing the continuous absorption or increasing the line strength Contribution Functions ∞ ∫ –∞ Fn = 2p Bn(tn) E2(tn) ln + kn t0 dlog t0 k0 log e Contribution function How does this behave with line strength and position in the line? Sample Contribution Functions Strong lines Weak line On average weaker lines are formed deeper in the atmosphere than stronger lines. For a given line the contribution to the line center comes from deeper in the atmosphere from the wings The fact that lines of different strength come from different depths in the atmosphere is often useful for interpreting observations. The rapidly oscillating Ap stars (roAp) pulsate with periods of 5–15 min. Radial velocity measurements show that weak lines of some elements pulsate 180 degres out-of-phase with strong lines. In stellar atmosphere: + ─ z Radial node where amplitude =0 Conclusion: The two lines are formed on opposite sides of a radial node where the amplitude of the pulsations is zero The mean amplitude versus mean equivalent width (line strength) of pulsations in the rapidly oscillating Ap star HD 101065 The mean amplitude versus phase of pulsations of the Balmer lines in the rapidly oscillating Ap star HD 101065 Ca II line The Ca II emission core in solar type active stars Dl (Å) Strong absorption lines are formed higher up in the stellar atmosphere. The core of the lines are formed even higher up (wings are formed deeper). Ca II is formed very high up in the atmospheres of solar type stars. Behavior of Spectral Lines The strength of a spectral line depends on: • Width of the absorption coefficient which is a function of thermal and microturbulent velocities • Number of absorbers (i.e. abundance) - Temperature - Electron Pressure - Atomic Constants Behavior of Spectral Lines: Temperature Dependence Temperature is the variable that most strongly controls the line strength because of the excitation and power dependences with T on the ionization and excitation processes Most lines go through a maximum • Increase with temperature is due to increase in excitation • Decrease beyond maximum can be due to an increase in continous opacity of negative hydrogen atom (increase in electron pressure) • With strong lines atomic absorption coefficient is proportional to g • Hydrogen lines have an absorption coefficient that is temperature sensitive through the stark effect Temperature Dependence Example: Cool star where kn behaves like the negative hydrogen ion‘s boundfree absorption: kn = constant T–5/2 Pee0.75/kT Four cases 1. Weak line of a neutral species with the element mostly neutral 2. Weak line of a neutral species with the element mostly ionized 3. Weak line of an ion with the element mostly neutral 4. Weak line of an ion with the element mostly ionized Behavior of Spectral Lines: Temperature Dependence Case #1: The number of absorbers in level l is given by : Nl = constant N0 e–c/kT ≈ constant e–c/kT The number of neutrals N0 is approximately constant with temperature until ionization occurs because the number of ions Ni is small compared to N0. Ratio of line to continuous absorption is: R= ln kn T5/2 –(c+0.75)/kT = constant e Pe Behavior of Spectral Lines: Temperature Dependence Recall that Pe = constant eWT 5 ln R = constant + 2 1 R dR dT ln T – c + 0.75 kT c + 0.75 2.5 – WT = + 2 T kT – WT Behavior of Spectral Lines: Temperature Dependence Exercise for the reader: Case 2 (neutral line, element ionized): 1 R dR dT = c + 0.75 – I kT2 Case 3 (ionic line, element neutral): 1 R dR dT = c + 0.75 + I 5 T + – 2WT kT2 Case 4 (ionic line, element ionized): 1 R dR dT 2.5 = T c + 0.75 + kT2 – WT Behavior of Spectral Lines: Temperature Dependence Exercise for the reader: Case 2 (neutral line, element ionized): 1 R dR dT = c + 0.75 – I kT2 Case 3 (ionic line, element neutral): 1 R dR dT = c + 0.75 + I 5 T + – 2WT kT2 Case 4 (ionic line, element ionized): 1 R dR dT 2.5 = T c + 0.75 + kT2 – WT The Behavior of Sodium D with Temperature The strength of Na D decreases with increasing temperature. In this case the absorption coeffiecent is proportional to g, which is a function of temperature Behavior of Hydrogen lines with temperature B3IV B9.5V A0 V G0V F0V The atomic absorption coefficient of hydrogen is temperature sensitve through the Stark effect. Because of the high excitation of the Balmer series (10.2 eV) this excitation growth continues to a maximum T = 9000 K Behavior of Spectral Lines: Pressure Dependence Pressure effects the lines in three ways 1. Ratio of line absorbers to the continous opacity (ionization equilibrium) 2. Pressure sensitivity of g for strong lines 3. Pressure dependence of Stark Broadening for hydrogen 2 For cool stars Pg ≈ constant Pe Pg ≈ constant g⅔ Pe ≈ constant g⅓ In other words, for F, G, and K stars the pressure dependencies are translated into gravity dependencies Gravity can influence both the line wings and the line strength Example of change in line strength with gravity Example of change in wings due to gravity Pressure dependence can be estimated by considering the ratio of line to continuous absorption coefficients Rules: 1. weak lines formed by any ion or atom where most of the element is in the next higher ionization stage are insenstive to pressure changes. 2. weak lines formed by any ion or atom where most of the element is in that same stage of ionization are presssure sensitive: lower pressure causes a greater line strength 3. weak lines formed by any ion or atom where most of the element is in the next lower ionization stage are very pressure sensitive: lower pressure causes a greater line strength. Rule #1 Ionization equation: Nr+1 Nr Fj(T) = Pe By rule one the line is formed in the rth ionization stage, but most of the element is in the Nr+1 ionization stage: Nr+1 ≈ Ntotal Nr ≈ constant Pe ln ≈ constant Nr ≈ constant Pe The line absortion coeffiecient is proportional to the number of absorbers The continous opacity from the negative hydrogen ion dominates: kn = constant T–5/2 Pee0.75/kT ln kn is independent of Pe Rule #2 If the line is formed by an element in the r ionization stage and most of this element is in the same stage, then Nr ≈ Ntotal ln kn = constant Pe ≈ constant g–⅓ Note: this change is not caused by a change in l, but because the continuum opacity of H– becomes less as Pe decreases Also note: ∂ log(ln/kn)/∂ log g = –0.33 Proof of rule #3 similar. In solar-type stars cases 1) and 2) are mostly encountered Behavior of Spectral Lines: Abundance Dependence The line strength should also depend on the abundance of the absorber, but the change in strength (equivalent width) is not a simple proportionality as it depends on the optical depth. 3 phases: Weak lines: the Doppler core dominates and the width is set by the thermal broadening DlD. Depth of the line grows in proportion to abundance A Saturation: central depth approches maximum value and line saturates towards a constant value Strong lines: the optical depth in the wings become significant compared to kn. The strength depends on g, but for constant g the equivalent width is proportional to A½ The graph specifying the change in equivalent width with abundance is called the Curve of Growth Behavior of Spectral Lines: Abundance Dependence Assume that lines are formed in a cool gas above the source of the continuum Fn = Fce–tn Fc is continuum flux L L ∫ tn = lnrdx = 0 0 ∫ Na dx L is the thickness of the cool gas. N/r = number of absorbers per unit mass N r N NE = NE NH NH r L tn = A 0 ∫ (N/NE)Nha dx N/NE is the fraction of element E capable of absorbing, NE/NH is the number abundance A, NH/r is the number of hydrogen atoms per unit mass tn is proportional to the abundance A and the flux varies exponentially with A Behavior of Spectral Lines: Abundance Dependence For weak lines tn << 1 Fn ≈ Fc(1 – tn) Fc – Fn Fc ≈ tn → line depth is proportional tn and thus A. The line depth and thus the equivalent width is proportional to A Behavior of Spectral Lines: Abundance Dependence What about strong lines? p½e2 f H(u,a) a= mc DnD The wings dominate so f pe2 g a= mc 4p2 DnD L tn = A 0 ∫ Af g (N/N )N dx (N/NE)Nha dx = E H 2 mc Dn2 4p 0 <g> A f h ≈ Dn2 pe2 L ∫ <g> denotes the depth average damping constant, and h is the constants and integral Fc – Fn Fc = 1 – e–tn The equivalent width of the line: ∞ W= 0 ∫ (1 – e–tn) dn ∞ W= 0 ∫ (1 – e–<g>Af h/Dn2) dn Substituting u2 = Dn2/<g>A f h ∞ W = (<g>A f h)½ 0 ∫ 2 (1 – e–1/u ) du Equivalent width is proportional to the square root of the abundance A bit of History Cecilia Payne-Gaposchkin (1900-1979). At Harvard in her Ph.D thesis on Stellar Atmospheres she: • Realized that Saha‘s theory of ionization could be used to determine the temperature and chemical composition of stars • Identified the spectral sequence as a temperature sequence and correctly concluded that the large variations in absorption lines seen in stars is due to ionization and not abundances • Found abundances of silicon, carbon, etc on sun similar to earth • Concluded that the sun, stars, and thus most of the universe is made of hydrogen and helium. Otto Struve: „undoubtedly the most brilliant Ph.D thesis ever written in Astronomy“ Youngest scientist to be listed in American Men of Science !!!