* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Current and Resistance
Nanogenerator wikipedia , lookup
Operational amplifier wikipedia , lookup
Giant magnetoresistance wikipedia , lookup
Surge protector wikipedia , lookup
Galvanometer wikipedia , lookup
Power MOSFET wikipedia , lookup
Resistive opto-isolator wikipedia , lookup
Superconductivity wikipedia , lookup
Nanofluidic circuitry wikipedia , lookup
Opto-isolator wikipedia , lookup
Rectiverter wikipedia , lookup
Current source wikipedia , lookup
Electromigration wikipedia , lookup
Electric charge wikipedia , lookup
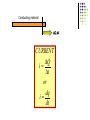
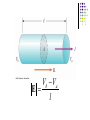
Current and Resistance February 22, 2006 Notes New topic today – Current and Resistance Exam – Friday – March 3 Through Chapter 27. No quiz on Friday. Watch for new WebAssign. A capacitor is constructed from two square plates of sides ℓ and separation d. A material of dielectric constant κ is inserted a distance x into the capacitor, as shown in the figure. Assume that d is much smaller than x. (a) Find the equivalent capacitance of the device. (b) Calculate the energy stored in the capacitor, letting ΔV represent the potential difference. (c) Find the direction and magnitude of the force exerted on the dielectric, assuming a constant potential difference ΔV. Ignore friction. (d) Obtain a numerical value for the force assuming that ℓ = 5.00 cm, ΔV = 2 000 V, d = 2.00 mm, and the dielectric is glass (κ = 4.50). Each capacitor in the combination shown in Figure P26.49 has a breakdown voltage of 15.0 V. What is the breakdown voltage of the combination? Current and Resistance Physical Resistors What Happens? IN TRUTH, THE ELECTRONS “+” “+” ARE ACTUALLY MOVING THE OTHER WAY! - “+” “+” DEFINITION Current is the motion of CHARGE through a circuit. Physically, it is electrons that move but … We define current as the motion of POSITIVE charge! (Blame you know who!) Conducting material DQ,Dt Conducting material DQ,Dt CURRENT DQ i Dt or dq i dt UNITS A current of one coulomb per second is defined as ONE AMPERE. A small sphere that carries a charge q is whirled in a circle at the end of an insulating string. The angular frequency of rotation is ω. What average current does this rotating charge represent? ANOTHER DEFINITION current I J area A Figure P27.8 represents a section of a circular conductor of non-uniform diameter carrying a current of 5.00 A. The radius of cross section A1 is 0.400 cm. (a) What is the magnitude of the current density across A1? (b) If the current density across A2 is one-fourth the value across A1, what is the radius of the conductor at A2? Ohm A particular object will resist the flow of current. It is found that for any conducting object, the current is proportional to the applied voltage. STATEMENT: DV=IR R is called the resistance of the object. An object that allows a current flow of one ampere when one volt is applied to it has a resistance of one OHM. Graph A DIODE Resistance Varies with Applied Voltage (actually with current) Let’s look at the atomic level .. Conduction is via electrons. They are weak and small and don’t exercise much. Positive charge is big and strong and doesn’t intimidate easily. It’s an ugly situation … something like …… + - Consider a metal conductor So far, we have said that a metal is an equipotential because no charges were moving. Hence, no electric field in the metal You can move a charge freely in the metal BECAUSE there is no electric field. NOW we have a current. This can only happen if we allow an electric field to push the charges. Thus, the metal is NO LONGER A TRUE EQUIPOTENTIAL. But almost …. as we shall see in the next chapter. Vb Va E l The Current Electrons are going the other way. They probably follow a path like … Average “drift” speed - vd Notation vd average drift velocity of the electron n number of electrons (mobile) per unit volume. Dt interval of time Dx average distance the electron moves in time Dt. Q total amount of CHARGE that goes through a surface of the conductor in time Dt. DQ (nAvd Dt )e DQ I avg nAvd e Dt I avg J nevd A J nev d Reference The average drift velocity of an electron is about 10-4 m/s Conductivity In metals, the bigger the electric field at a point, the bigger the current density. J E is the conductivity of the material. r=(1/) is the resistivity of the material Going to the usual limit … dI J dA and I JdA Example A cylindrical conductor of radius R has a current density given by (a) J0 (constant) (b) gr Find the total current in each case. r r0 1 (T T0 ) Range of r and Ye old RESISTANCE DV El 1 DV 1 DV I J E E r El r l A rl DV I A rl R A DV V IR Additional Topics Power Micro basis of conduction.