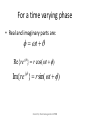Download Electromagnetic Intro

Electromagnetism
INEL 4151
Ch 10 Waves
Sandra Cruz-Pol, Ph. D.
ECE UPRM
Mayagüez, PR
Cruz-Pol, Electromagnetics UPRM
Electromagnetic Spectrum
Cruz-Pol, Electromagnetics UPRM
Maxwell Equations
in General Form
Differential form Integral Form
  D  v
 D  dS   v dv
s
 B  0
v
 B  dS  0
s
B
 E  
t
D
 H  J 
t
Gauss’s Law for E
field.
Gauss’s Law for H
field. Nonexistence
of monopole

Faraday’s Law
L E  dl   t s B  dS
D 

H

dl

J


L
s  t   dS
Cruz-Pol, Electromagnetics UPRM
Ampere’s Circuit
Law
Who was NikolaTesla?
• Find out what inventions he made
• His relation to Thomas Edison
• Why is he not well know?
Cruz-Pol, Electromagnetics UPRM
Special case
• Consider the case of a lossless medium
 0
• with no charges, i.e. .
v  0
The wave equation can be derived from Maxwell
equations as
 E    c E  0
2
2
What is the solution for this differential equation?
• The equation of a wave!
Cruz-Pol, Electromagnetics UPRM
Phasors & complex #’s
Working with harmonic fields is easier, but
requires knowledge of phasor, let’s review
• complex numbers and
• phasors
Cruz-Pol, Electromagnetics UPRM
COMPLEX NUMBERS:
• Given a complex number z
z  x  jy  re
where
j
 r  r cos   jr sin 
r | z | x  y is the magnitude
2
  tan
1
2
y
is the angle
x
Cruz-Pol, Electromagnetics UPRM
Review:
•
•
•
•
•
•
Addition,
Subtraction,
Multiplication,
Division,
Square Root,
Complex Conjugate
Cruz-Pol, Electromagnetics UPRM
For a time varying phase
• Real and imaginary parts are:
  t  
j
Re{re }  r cos(t   )
j
Im{re }  r sin( t   )
Cruz-Pol, Electromagnetics UPRM
PHASORS
• For a sinusoidal current I (t )  I o cos(t   )
j jt
equals the real part of I o e e
j
I
e
• The complex term o which results from
jt
dropping the time factor e is called the
I(ss comes from
phasor current, denoted by
sinusoidal)
Cruz-Pol, Electromagnetics UPRM
To change back to time domain
• The phasor is multiplied by the time factor,
ejt, and taken the real part.
A  Re{ As e
jt
}
Cruz-Pol, Electromagnetics UPRM
Advantages of phasors
• Time derivative is equivalent to multiplying its
phasor by j
A
 jAs
t
• Time integral is equivalent to dividing by the
same term.
As
 At  j
Cruz-Pol, Electromagnetics UPRM
Time-Harmonic fields
(sines and cosines)
• The wave equation can be derived from
Maxwell equations, indicating that the
changes in the fields behave as a wave, called
an electromagnetic field.
• Since any periodic wave can be represented as
a sum of sines and cosines (using Fourier),
then we can deal only with harmonic fields to
simplify the equations.
Cruz-Pol, Electromagnetics UPRM
Maxwell Equations
for Harmonic fields
Differential form*

 DE
 v  v
Gauss’s Law for E field.
 BH
0

Gauss’s Law for H field.
No monopole
0
  E   jH
 E  
B
t
  H  J  jE
D
 H  J 
t
* (substituting
Faraday’s Law
Ampere’s Circuit Law
D   E and
H Electromagnetics
B )
Cruz-Pol,
UPRM
A wave
• Start taking the curl of Faraday’s law
    Es   j  H s
• Then apply the vectorial identity
    A  (  A)   2 A
• And you’re left with
(  Es )   Es   j (  j ) Es
2
  Es
2
Cruz-Pol, Electromagnetics UPRM
A Wave
 E  E  0
2
2
Let’s look at a special case for simplicity
without loosing generality:
•The electric field has only an x-component
•The field travels in z direction
Then we have
E ( z, t )
whose general solution is
E(z)  Eo e z  Eo' e z
Cruz-Pol, Electromagnetics UPRM
To change back to time domain
• From phasor
E xs ( z )  Eo e
 z
 Eo e
 z (  j )
• …to time domain
E ( z , t )  Eo e
 z

cos(t  z ) x
Cruz-Pol, Electromagnetics UPRM
Several Cases of Media
1.
2.
3.
4.
(  0,    o ,   o )
Free space
Lossless dielectric
(  0,    r  o ,    r o or    )
Lossy dielectric
(  0,    r  o ,    r o )
Good Conductor
(  ,    o ,    r o or    )
o=8.854 x 10-12[ F/m]
o= 4p x 10-7 [H/m]
Cruz-Pol, Electromagnetics UPRM
1. Free space
There are no losses, e.g.

E ( z, t )  A sin( t  z ) x
Let’s define
• The phase of the wave
• The angular frequency
• Phase constant
• The phase velocity of the wave
• The period and wavelength
• How does it moves?
Cruz-Pol, Electromagnetics UPRM
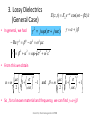
3. Lossy Dielectrics
(General Case)
• In general, we had

E ( z , t )  Eo e z cos(t  z ) x
 2  j (  j )
    j
 Re  2   2   2   2 
 2   2   2    2   2 2
• From this we obtain
2
2










 1  
 1  
 
  1 and   
  1
2 
 
2 
 








• So , for a known material and frequency, we can find j
Cruz-Pol, Electromagnetics UPRM
Intrinsic Impedance, h
• If we divide E by H, we get units of ohms and the
definition of the intrinsic impedance of a medium
at a given frequency.
j
 h h
h
  j
E ( z, t )  Eo e
H ( z, t ) 
Eo
h
z
[]

cos(t  z ) x
e z cos(t  z  h ) yˆ
Cruz-Pol, Electromagnetics UPRM
*Not in-phase
for a lossy
medium
Note…
E ( z, t )  Eo e
H ( z, t ) 
Eo
h
z

cos(t  z ) x
e z cos(t  z  h ) yˆ
• E and H are perpendicular to one another
• Travel is perpendicular to the direction of
propagation
• The amplitude is related to the impedance
• And so is the phase
Cruz-Pol, Electromagnetics UPRM
Loss Tangent
• If we divide the conduction current by the
displacement current
J cs
J ds
 Es



 tan   loss tangent
j Es 
http://fipsgold.physik.uni-kl.de/software/java/polarisation
Cruz-Pol, Electromagnetics UPRM
Relation between tan and c
 

  H  E  j E  j 1  j
E

 

 j c E
The complex permittivi ty is
 

 c   1  j    ' j ' '
 

" 
The loss tangent can be defined also as tan   
 ' 
Cruz-Pol, Electromagnetics UPRM
2. Lossless dielectric
(  0,    r  o ,   r o or    )
• Substituting in the general equations:
  0,    

1
2p
u 




 o
h
0

Cruz-Pol, Electromagnetics UPRM
Review: 1. Free Space
(  0,    o ,   o )
• Substituting in the general equations:
  0,       / c

1
2p
u 
c



 o o
h
o o
0  120p   377 
o

E ( z , t )  Eo cos(t  z ) x V / m
H ( z, t ) 
Eo
ho
cos(t  z ) yˆ
A/ m
Cruz-Pol, Electromagnetics UPRM
4. Good Conductors
(  ,    o ,   r o )
• Substituting in the general equations:
  


2
u 


2

2p
Is water a good
conductor???


h
45o


E ( z , t )  Eo e z cos(t  z ) x [V / m]
H ( z, t ) 
Eo
e z cos(t  z  45o ) yˆ [ A / m]

 Electromagnetics
Cruz-Pol,
UPRM
o
Summary
Lossless
medium
(=0)
Any medium


2

 

 1 
  1
2 







h
uc

0
 
Low-loss medium
(”/’<.01)



2
Good conductor
(”/’>100)
Units
[Np/m]
pf
[rad/m]
 
 
pf

(1  j )

j
  j


/
1
1
4pf



2p/up/f
**In free space;


up
up
up
f
f
f
-7
oCruz-Pol,
=8.85Electromagnetics
x 10-12 F/m
UPRM o=4p x 10 H/m
[ohm]
[m/s]
[m]
Skin depth, d
• Is defined as the depth
at which the electric
amplitude is decreased
to 37%
1
e  0.37  (37%)
e
z
e
1
at z  1 /   d
d  1 /  [m]
Cruz-Pol, Electromagnetics UPRM
Short Cut …
• You can use Maxwell’s or use
 1

H  kˆ  E
h


E  h kˆ  H
where k is the direction of propagation of the wave, i.e.,
the direction in which the EM wave is traveling (a
unitary vector).
Cruz-Pol, Electromagnetics UPRM
Waves
• Static charges > static electric field, E
• Steady current > static magnetic field, H
• Static magnet > static magnetic field, H
• Time-varying current > time varying E(t) & H(t) that are
interdependent > electromagnetic wave
• Time-varying magnet > time varying E(t) & H(t) that are
interdependent > electromagnetic wave
Cruz-Pol, Electromagnetics UPRM
EM waves don’t need a medium to
propagate
• Sound waves need a
medium like air or water to
propagate
• EM wave don’t. They can
travel in free space in the
complete absence of matter.
• Look at a “wind wave”; the
energy moves, the plants
stay at the same place.
Cruz-Pol, Electromagnetics UPRM
Exercises: Wave Propagation in
Lossless materials
•
A wave in a nonmagnetic material is given by

H  zˆ50 cos(109 t  5 y ) [mA/m]
Find:
(a) direction of wave propagation,
(b) wavelength in the material
(c) phase velocity
(d) Relative permittivity of material
(e) Electric field phasor
Answer: +y, up= 2x108 m/s, 1.26m, 2.25,
Cruz-Pol, Electromagnetics UPRM

E   xˆ12.57e  j 5 y [V/m]
Power in a wave
• A wave carries power and transmits it wherever it
goes
The power density per
area carried by a wave
is given by the
Poynting vector.
See Applet by Daniel Roth at
Cruz-Pol, Electromagnetics UPRM
http://fipsgold.physik.uni-kl.de/software/java/polarisation
Poynting Vector Derivation
• Start with E dot Ampere
E 

E    H  E  
t 

E    H   E  E  E  
• Apply vectorial identity
   A  B   B    A  A    B  or in this case :
  H  E   E    H   H    E 
• And end up with
1 E
H    E     H  E   E  
2 t
2
Cruz-Pol, Electromagnetics UPRM
2
E
t
Poynting Vector Derivation…
• Substitute Faraday in 1rst term
H 
1 E 2

2
H  
    H  E   E  

t
2 t


H   H  H 

As in derivative of square function : H    

t  2
t

and if invert the order, it' s (-)
  H  E     E  H 

 H 2
2 t
   E  H   E 2 
 E 2
2 t
Rearrange
  E 2  H 2 
  E 2
  E  H   

t Electromagnetics
2 t  UPRM
 2Cruz-Pol,
Poynting Vector Derivation…
• Taking the integral wrt volume
   E  H dv  
v
  2  2
2
E

H
dv


E
dv




t v  2
2

v
• Applying theory of divergence
  2  2
2


E

H

dS


E

H
dv


E
dv


S


t v  2
2

v
Total power across
surface of volume
Rate of change of
stored energy in E or H
Ohmic losses due to
conduction current
• Which simply means that the total power coming out of a
volume is either due to the electric or magnetic field energy
variations or is lost in ohmic losses.
Cruz-Pol, Electromagnetics UPRM
Power: Poynting Vector
• Waves carry energy and information
• Poynting says that the net power flowing out of a
given volume is = to the decrease in time in energy
stored minus the conduction losses.
  
P  EH
2
[W/m ]
Cruz-Pol, Electromagnetics UPRM
Represents the
instantaneous
power vector
associated to the
electromagnetic
wave.
Time Average Power
• The Poynting vector averaged in time is



T
T 

 *


1
1
1
Pave   P dt   E  H dt  Re Es  H s
T0
T0
2

• For the general case wave:
Es  Eo e z e  jz xˆ [V / m]
Hs 
Eo
h
e z e  jz yˆ [ A / m]
Pave
Eo2  2z

e
cos h zˆ
2h
Cruz-Pol, Electromagnetics UPRM
[W/m 2 ]
Total Power in W
The total power through a surface S is

Pave   Pave  dS [W ]
S
• Note that the units now are in Watts
• Note that power nomenclature, P is not cursive.
• Note that the dot product indicates that the surface area
needs to be perpendicular to the Poynting vector so that
all the power will go thru. (give example of receiver
antenna)
Cruz-Pol, Electromagnetics UPRM
Exercises: Power
1. At microwave frequencies, the power density considered
safe for human exposure is 1 mW/cm2. A radar radiates a
wave with an electric field amplitude E that decays with
distance as E(R)=3000/R [V/m], where R is the distance
in meters. What is the radius of the unsafe region?
• Answer: 34.64 m
2. A 5GHz wave traveling In a nonmagnetic medium with
r=9 is characterized by E  yˆ 3 cos(t  x)  zˆ 2 cos(t  x)[V/m]
Determine the direction of wave travel and the average
power density carried by the wave
• Answer: 
Pave   xˆ 0.05 [W/m 2 ]
Cruz-Pol, Electromagnetics UPRM
x
TEM wave
x
z
z
y
Transverse ElectroMagnetic = plane wave
• There are no fields parallel to the direction of
propagation,
• only perpendicular (transverse).
• If have an electric field Ex(z)
– …then must have a corresponding magnetic field
Hx(z)
• The direction of propagation is
– aE x aH = a k
Cruz-Pol, Electromagnetics UPRM
PE 10.7
In free space, H=0.2 cos (t-x) z A/m. Find the
total power passing through a
• square plate of side 10cm on plane x+z=1
x
Answer; Ptot = 53mW
Hz
• square plate at x=1, 0
Ey
Answer; Ptot = 0mW!
Cruz-Pol, Electromagnetics UPRM
Polarization of a wave
IEEE Definition:
The trace of the tip of the Efield vector as a function of
time seen from behind.
x
x
Simple cases
• Vertical, Ex
y
y
x
Exs ( z )  Eo e
 jz
Ex ( z )  Eo cos(t  z ) xˆ
• Horizontal, Ey
y
y
Cruz-Pol, Electromagnetics UPRM
x
Dual-Pol in Weather Radars
Lineal Typical
•Horizontal
•Vertical
ZHH ZVV
ZHV ZVH
Dra. Leyda León
• Dual polarization radars can
estimate several return
signal properties beyond
those available from
conventional, single
polarization Doppler
systems.
• Hydrometeors: Shape,
Direction, Behavior, Type,
etc…
• Events: Development,
identification, extinction
Polarization:
Why do we care??
• Antenna applications –
– Antenna can only TX or RX a polarization it is designed to support. Straight
wires, square waveguides, and similar rectangular systems support linear
waves (polarized in one direction, often) Round waveguides, helical or flat
spiral antennas produce circular or elliptical waves.
• Remote Sensing and Radar Applications –
– Many targets will reflect or absorb EM waves differently for different
polarizations. Using multiple polarizations can give different information
and improve results.
• Absorption applications –
– Human body, for instance, will absorb waves with E oriented from head to
toe better than side-to-side, esp. in grounded cases. Also, the frequency at
which maximum absorption occurs is different for these two polarizations.
This has ramifications in safety guidelines and studies.
Cruz-Pol, Electromagnetics UPRM
Polarization
• In general, plane wave has 2 components; in x & y
E ( z )  xˆE x  yˆE y
• And y-component might be out of phase wrt to x-component, d is
the phase difference between x and y.
E x  Eo e
 j z
x
E y  E o e  j z  d
Ex
x
y
y
Cruz-Pol, Electromagnetics UPRM
Ey
Front View
Several Cases
• Linear polarization: ddy-dx =0o or ±180on
• Circular polarization: dy-dx =±90o & Eox=Eoy
• Elliptical polarization: dy-dx=±90o & Eox≠Eoy,
or d≠0o or ≠180on even if Eox=Eoy
• Unpolarized- natural radiation
Cruz-Pol, Electromagnetics UPRM
Linear polarization
Front View
• d =0
x
E x  E o e  j z
E y  E o e  j z
Ex
y
Ey
• @z=0 in time domain
E x  E xo cos(t)
E y  E yo cos(t)
Back View:
x
y
Cruz-Pol, Electromagnetics UPRM
Circular polarization
• Both components have
same amplitude Eox=Eoy,
• d =d y-d x= -90o = Right
circular polarized (RCP)
• d =+90o = LCP
E x  E xo cos(t)
E y  E yo cos(t  90 o )
in phasor :
E  xˆE xo  yˆ E yo e  j 90  xˆE xo  jE yo yˆ
Cruz-Pol, Electromagnetics UPRM
Elliptical polarization
• X and Y components have different amplitudes
Eox≠Eoy, and d =±90o
• Or d ≠±90o and Eox=Eoy,
Cruz-Pol, Electromagnetics UPRM
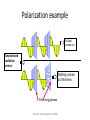
Polarization example
All light
comes out
Unpolarized
radiation
enters
Nothing comes
out this time.
Polarizing glasses
Cruz-Pol, Electromagnetics UPRM
sin(  180
sin( ))
90 ))  cos(
oo
Example
cos(( 180
90 ))  scos
in (())
oo
• Determine the polarization state of a plane wave with
electric field:
a. E ( z, t )  xˆ3cos(t - z  30o ) - ŷ4sin( t - z  45o )
b. E ( z, t )  xˆ3cos(t - z  45o )  ŷ8sin( t - z  45o )
o
o
ˆ
E
(
z
,
t
)

x
4
cos(

t

z

45
)
ŷ
4sin(

t

z

45
)
c.
d. Es =14( x̂ - jẑ)e
-jb y
a.
Elliptic
b.
-90, RHEP
c.
+90, LHCP
Cruz-Pol, Electromagnetics UPRM
d.
-90, RHCP
Cell phone & brain
• Computer model for
Cell phone Radiation
inside the Human Brain
Cruz-Pol, Electromagnetics UPRM
Radar bands
Band Name
Nominal Freq
Range
HF, VHF, UHF
3-30 MHz0, 30-300 MHz, 3001000MHz
Specific Bands
138-144 MHz
216-225, 420-450 MHz
890-942
Application
TV, Radio,
Clear air, soil moist
L
1-2 GHz (15-30 cm)
1.215-1.4 GHz
S
2-4 GHz (8-15 cm)
2.3-2.5 GHz
2.7-3.7>
C
4-8 GHz (4-8 cm)
5.25-5.925 GHz
TV stations, short range
Weather
X
8-12 GHz (2.5–4 cm)
8.5-10.68 GHz
Cloud, light rain, airplane
weather. Police radar.
Ku
12-18 GHz
13.4-14.0 GHz, 15.7-17.7
K
18-27 GHz
24.05-24.25 GHz
Ka
27-40 GHz
33.4-36.0 GHz
V
40-75 GHz
59-64 GHz
W
75-110 GHz
76-81 GH, 92-100 GHz
Weather observations
Cellular phones
Weather studies
Water vapor content
Cloud, rain
Intra-building comm.
Rain, tornadoes
Cruz-Pol, Electromagnetics UPRM
millimeter
110-300 GHz
Tornado chasers
Microwave Oven
Most food is lossy media at
microwave frequencies,
therefore EM power is lost in
the food as heat.
 c   o (30  j1)
• Find depth of penetration if
chicken which at 2.45 GHz has
the complex permittivity given.

The power reaches the inside as
soon as the oven in turned on!
2pf

( j  30)
c
 4.7  j 281 [/m]
j o j c
d  1/   21.3 cm
Cruz-Pol, Electromagnetics UPRM
Decibel Scale
• In many applications need comparison of two powers,
a power ratio, e.g. reflected power, attenuated power,
gain,…
• The decibel (dB) scale is logarithmic
G
P1
P2
 V12 /R 
 P1 
V 
G[dB]  10 log    10 log  2   20 log  1 
 P2 
 V2 
 V2 /R 
• Note that for voltages, the log is multiplied by 20
instead of 10.
Cruz-Pol, Electromagnetics UPRM
Attenuation rate, A
• Represents the rate of decrease of the magnitude of
Pave(z) as a function of propagation distance
 Pave(z) 
  10 log e 2z
A  10 log 
 Pave( 0 ) 
 20z log e  - 8.68z  - dB z [dB]

where
 dB[dB/m ]  8.68 [ Np/m]
Cruz-Pol, Electromagnetics UPRM

Submarine antenna
A submarine at a depth of 200m uses a wire
antenna to receive signal transmissions at
1kHz.
• Determine the power density incident upon
the submarine antenna due to the EM wave
with |Eo|= 10V/m.
• [At 1kHz, sea water has r=81, =4].
Pave
Eo2  2z

e
cos h zˆ
2h
[W/m 2 ]
• At what depth the amplitude of E has
decreased to 1% its initial value at z=0 (sea
surface)?
Cruz-Pol, Electromagnetics UPRM
Exercise: Lossy media propagation
For each of the following determine if the material is low-loss dielectric,
good conductor, etc.
(a) Glass with r=1, r=5 and =10-12 S/m at 10 GHZ
(b) Animal tissue with r=1, r=12 and =0.3 S/m at 100 MHZ
(c) Wood with r=1, r=3 and =10-4 S/m at 1 kHZ
Answer:
(a)
(b)
(c)
low-loss,  8.4x1011 Np/m,  468 r/m,  1.34 cm, up1.34x108, hc168 
general,  9.75, 12, 52 cm, up0.5x108 m/s, hc39.5j31.7 
Good conductor,  6.3x104,  6.3x104,  10km, up0.1x108, hc6.281j 
Cruz-Pol, Electromagnetics UPRM