Download Electric potential energy

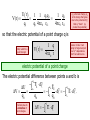
Today’s agenda:
Electric potential energy.
You must be able to use electric potential energy in work-energy calculations.
Electric potential.
You must be able to calculate the electric potential for a point charge, and use the electric
potential in work-energy calculations.
Electric potential and electric potential energy of a system of
charges.
You must be able to calculate both electric potential and electric potential energy for a
system of charged particles (point charges today, charge distributions next lecture).
The electron volt.
You must be able to use the electron volt as an alternative unit of energy.
Now I’m going to do something different, and introduce the
“electric potential.”
Electric potential energy is “just like” gravitational potential
energy.
Except that all matter exerts an attractive gravitational force, but charged particles exert
either attractive or repulsive electrical forces—so we need to be careful with our signs.
Electric potential is the electric potential energy per unit of
charge.
Electric Potential
In lecture 1 we defined the electric field by the force it exerts
on a test charge q0:
F0
E = lim
q 0 0 q
0
Similarly, it is useful to define the potential in terms of the
potential energy of a test charge q0:
Ur
V  r  = lim
q 0 0
q0
Later you’ll get an Official
Starting Equation version of this.
The electric potential V is independent of the test charge q0.
A point in space can have an electric potential even if there is no charge around to “feel” it.
U r
1 1 q1q 2
1 q2
V(r) 


q1
q1 40 r12
40 r12
q1 is the test charge, q2
is the charge that gives
rise to the potential V(r)
that q1 “feels.” (q1
probes the potential)
so that the electric potential of a point charge q is
Only valid for a
point charge!
1 q
V r 
.
40 r
Sooner or later I am
going to forget and put
in a 1/r2 dependence.
Don’t be bad like me.
electric potential of a point charge
The electric potential difference between points a and b is
rb
rb F
rb
U  ra FE  d
E
V 

 
 d   E  d .
ra q
ra
q0
q0
0
E is likely due to
a collection of
point charges.
f
V   E  d
i
One more starting equation
rb
rb F
rb
U  ra FE  d
E
V 

 
 d   E  d .
ra q
ra
q0
q0
0
U
V  Vf  Vi 
q
*Very Handy Version: U  q V
Copied from
previous slide.
Drop the subscript on the
q0. It was there to remind us
that q0 is the charge that
“feels” the potential.
A particle of charge q moved through a
potential difference V gains (or loses)
potential energy q V.
*In other words, you usually start with this version of the equation.
Things to remember about electric potential:
 Electric potential and electric potential energy are related, but
not the same.
Electric potential difference is the work per unit of charge
that must be done to move a charge from one point to
another without changing its kinetic energy.
 The terms “electric potential” and “potential” are used
interchangeably.
Ur
.
 The units of potential are joules/coulomb: V  r  =
q0
1 joule
1 volt =
1 coulomb
Things to remember about electric potential:
 Only differences in electric potential and electric potential
energy are meaningful.
It is always necessary to define where U and V are zero. In
this lecture we define V to be zero at an infinite distance
from the sources of the electric field.
Sometimes (e.g., circuits) it is convenient to define V to be
zero at the earth (ground).
It will be clear from the context where V is defined to be
zero. Most equations for this chapter assume V=0 at infinite
separation of charges.
Saying “take V to be zero when the charges are far apart means “it’s OK to use the equations in this chapter.”
Two conceptual examples.
Example: a proton is released in a region in space where there
is an electric potential. Describe the subsequent motion of the
proton.
The proton will move towards the region of lower potential. As it moves, its
potential energy will decrease, and its kinetic energy and speed will increase.
Example: a electron is released in a region in space where there
is an electric potential. Describe the subsequent motion of the
electron.
The electron will move towards the region of higher potential. As it moves,
its potential energy will decrease, and its kinetic energy and speed will
increase.
Protons fall down, electrons fall up.
What is the potential due to the proton in the hydrogen atom at
the electron’s position (5.29x10-11 m away from the proton)?
27.2V
To be worked at the blackboard in lecture.
Important note:
V
this is the symbol for electrical potential
V
this is the symbol for the unit (volts) of electrical
potential
v
this is the symbol for magnitude of velocity, or speed
Don’t get your v’s and V’s mixed up! Hint: write your speed v’s
as script v’s, like this (or however you want to clearly indicate a
lowercase v):
v 
vv
What is the potential due to the proton in the hydrogen atom at
the electron’s position (5.29x10-11 m away from the proton)?
27.2V
+e
+
-e
P
-
VP?
D



kq
k  e
9 109  1.6 109
Vp 


 27.2 V
11
r
D
5.29 10


In the second part of today’s lecture…
I defined electric potential as potential energy per unit of
charge
U  q V
This equation also lets you calculate the
change in potential energy when a charge
q moves through a potential difference V.
…and found the potential due to a point charge…
1 q
V r 
40 r
…and showed how to calculate the potential difference
between two points in an electric field
f
V   E  d .
i
We haven’t used this yet, but will eventually.