* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download DHTs
Survey
Document related concepts
Transcript
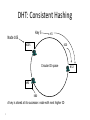
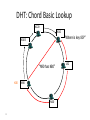
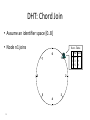
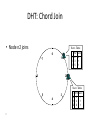
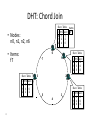
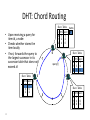
Distributed Hash Tables Parallel and Distributed Computing Spring 2011 [email protected] 1 Distributed Hash Tables • Academic answer to p2p • Goals – Guaranteed lookup success – Provable bounds on search time – Provable scalability • Makes some things harder – Fuzzy queries / full-text search / etc. • Hot Topic in networking since introduction in ~2000/2001 2 DHT: Overview • Abstraction: a distributed “hash-table” (DHT) data structure supports two operations: – put(id, item); – item = get(id); • Implementation: nodes in system form a distributed data structure – Can be Ring, Tree, Hypercube, Skip List, Butterfly Network, ... 3 What Is a DHT? • A building block used to locate key-based objects over millions of hosts on the internet • Inspired from traditional hash table: – key = Hash(name) – put(key, value) – get(key) -> value • Challenges – Decentralized: no central authority – Scalable: low network traffic overhead – Efficient: find items quickly (latency) – Dynamic: nodes fail, new nodes join – General-purpose: flexible naming 4 The Lookup Problem N1 Put (Key=“title” Value=file data…) Publisher N2 Internet N4 N5 N3 ? Client Get(key=“title”) N6 5 DHTs: Main Idea N2 N1 Publisher N4 Key=H(audio data) Value={artist, album title, track title} N6 N7 N3 Client Lookup(H(audio data)) N8 N9 6 DHT: Overview (2) • Structured Overlay Routing: – Join: On startup, contact a “bootstrap” node and integrate yourself into the distributed data structure; get a node id – Publish: Route publication for file id toward a close node id along the data structure – Search: Route a query for file id toward a close node id. Data structure guarantees that query will meet the publication. – Fetch: Two options: • Publication contains actual file => fetch from where query stops • Publication says “I have file X” => query tells you 128.2.1.3 has X, use IP routing to get X from 128.2.1.3 7 From Hash Tables to Distributed Hash Tables Challenge: Scalably distributing the index space: – Scalability issue with hash tables: Add new entry => move many items – Solution: consistent hashing (Karger 97) Consistent hashing: – Circular ID space with a distance metric – Objects and nodes mapped onto the same space – A key is stored at its successor: node with next higher ID 8 DHT: Consistent Hashing Key 5 Node 105 K5 N105 K20 Circular ID space N90 K80 A key is stored at its successor: node with next higher ID 9 N32 What Is a DHT? • Distributed Hash Table: key = Hash(data) lookup(key) -> IP address put(key, value) get( key) -> value • API supports a wide range of applications – DHT imposes no structure/meaning on keys • Key/value pairs are persistent and global – Can store keys in other DHT values – And thus build complex data structures 10 Approaches • Different strategies – Chord: constructing a distributed hash table – CAN: Routing in a d-dimensional space – Many more… • Commonalities – Each peer maintains a small part of the index information (routing table) – Searches performed by directed message forwarding • Differences – Performance and qualitative criteria 11 DHT: Example - Chord • Associate to each node and file a unique id in an unidimensional space (a Ring) – E.g., pick from the range [0...2m-1] – Usually the hash of the file or IP address • Properties: – Routing table size is O(log N) , where N is the total number of nodes – Guarantees that a file is found in O(log N) hops 12 Example 1: Distributed Hash Tables (Chord) • Hashing of search keys AND peer addresses on binary keys of length m – Key identifier = SHA-1(key); Node identifier = SHA-1(IP address) – SHA-1 distributes both uniformly – e.g. m=8, key(“yellow-submarine.mp3")=17, key(192.178.0.1)=3 • Data keys are stored at next larger node key p peer with hashed identifier p, data with hashed identifier k k stored at node p such that p is the smallest node ID larger than k k predecessor m=8 stored 32 keys at p2 p3 Search possibilities? 1. every peer knows every other O(n) routing table size 2. peers know successor O(n) search cost 13 DHT: Chord Basic Lookup N120 N10 “Where is key 80?” N105 “N90 has K80” K80 N90 N60 14 N32 DHT: Chord “Finger Table” 1/4 1/2 1/8 1/16 1/32 1/64 1/128 N80 • Entry i in the finger table of node n is the first node that succeeds or equals n + 2i • In other words, the ith finger points 1/2n-i way around the ring 15 DHT: Chord Join • Assume an identifier space [0..8] • Node n1 joins Succ. Table i id+2i succ 0 2 1 1 3 1 2 5 1 0 1 7 6 2 5 3 4 16 DHT: Chord Join • Node n2 joins Succ. Table i id+2i succ 0 2 2 1 3 1 2 5 1 0 1 7 6 2 Succ. Table 5 3 4 17 i id+2i succ 0 3 1 1 4 1 2 6 1 DHT: Chord Join Succ. Table i id+2i succ 0 1 1 1 2 2 2 4 0 • Nodes n0, n6 join Succ. Table i id+2i succ 0 2 2 1 3 6 2 5 6 0 1 7 Succ. Table i id+2i succ 0 7 0 1 0 0 2 2 2 6 2 Succ. Table 5 3 4 18 i id+2i succ 0 3 6 1 4 6 2 6 6 DHT: Chord Join Succ. Table i i id+2 0 1 1 2 2 4 • Nodes: n0, n1, n2, n6 • Items: f7 0 i id+2i succ 0 7 0 1 0 0 2 2 2 Succ. Table 1 7 Succ. Table 6 i id+2i succ 0 2 2 1 3 6 2 5 6 2 Succ. Table 5 3 4 19 Items f7 succ 1 2 0 i id+2i succ 0 3 6 1 4 6 2 6 6 DHT: Chord Routing Succ. Table • Upon receiving a query for item id, a node: • Checks whether stores the item locally • If not, forwards the query to the largest successor in its successor table that does not exceed id Succ. Table i id+2i succ 0 7 0 1 0 0 2 2 2 i i id+2 0 1 1 2 2 4 0 Succ. Table 1 7 i id+2i succ 0 2 2 1 3 6 2 5 6 query(7) 6 2 Succ. Table 5 3 4 20 Items f7 succ 1 2 0 i id+2i succ 0 3 6 1 4 6 2 6 6 DHT: Chord Summary • Routing table size? –Log N fingers • Routing time? –Each hop expects to 1/2 the distance to the desired id => expect O(log N) hops. 21 Load Balancing in Chord Network size n=10^4 5 10^5 keys 22 Length of Search Paths Network size n=2^12 100 2^12 keys Path length ½ Log2(n) 23 Chord Discussion • Performance – – – – – – Search latency: O(log n) (with high probability, provable) Message Bandwidth: O(log n) (selective routing) Storage cost: O(log n) (routing table) Update cost: low (like search) Node join/leave cost: O(Log2 n) Resilience to failures: replication to successor nodes • Qualitative Criteria – search predicates: equality of keys only – global knowledge: key hashing, network origin – peer autonomy: nodes have by virtue of their address a specific role in the network 24 Example 2: Topological Routing (CAN) • Based on hashing of keys into a d-dimensional space (a torus) – Each peer is responsible for keys of a subvolume of the space (a zone) – Each peer stores the addresses of peers responsible for the neighboring zones for routing – Search requests are greedily forwarded to the peers in the closest zones • Assignment of peers to zones depends on a random selection made by the peer 25 Network Search and Join Node 7 joins the network by choosing a coordinate in the volume of 1 26 CAN Refinements • Multiple Realities – We can have r different coordinate spaces – Nodes hold a zone in each of them – Creates r replicas of the (key, value) pairs – Increases robustness – Reduces path length as search can be continued in the reality where the target is closest • Overloading zones – Different peers are responsible for the same zone – Splits are only performed if a maximum occupancy (e.g. 4) is reached – Nodes know all other nodes in the same zone – But only one of the neighbors 27 CAN Path Length 28 Increasing Dimensions and Realities 29 CAN Discussion • Performance – Search latency: O(d n1/d), depends on choice of d (with high probability, provable) – Message Bandwidth: O(d n1/d), (selective routing) – Storage cost: O(d) (routing table) – Update cost: low (like search) – Node join/leave cost: O(d n1/d) – Resilience to failures: realities and overloading • Qualitative Criteria – search predicates: spatial distance of multidimensional keys – global knowledge: key hashing, network origin – peer autonomy: nodes can decide on their position in the key space 30 Comparison of some P2P Solutions Search Paradigm Overlay maintenance costs Search Cost TTL 2* i 0 C *(C 1)i Gnutella Breadth-first O(1) on search graph Chord Implicit binary search trees O(log n) O(log n) CAN d-dimensional space O(d) O(d n1/d) DHT Applications Not only for sharing music anymore… – Global file systems [OceanStore, CFS, PAST, Pastiche, UsenetDHT] – Naming services [Chord-DNS, Twine, SFR] – DB query processing [PIER, Wisc] – Internet-scale data structures [PHT, Cone, SkipGraphs] – Communication services [i3, MCAN, Bayeux] – Event notification [Scribe, Herald] – File sharing [OverNet] 32 DHT: Discussion • Pros: – Guaranteed Lookup – O(log N) per node state and search scope • Cons: – No one uses them? (only one file sharing app) – Supporting non-exact match search is hard 33 When are p2p / DHTs useful? • Caching and “soft-state” data – Works well! BitTorrent, KaZaA, etc., all use peers as caches for hot data • Finding read-only data – Limited flooding finds hay – DHTs find needles • BUT 34 A Peer-to-peer Google? • Complex intersection queries (“the” + “who”) – Billions of hits for each term alone • Sophisticated ranking – Must compare many results before returning a subset to user • Very, very hard for a DHT / p2p system – Need high inter-node bandwidth – (This is exactly what Google does - massive clusters) 35 Writable, persistent p2p • Do you trust your data to 100,000 monkeys? • Node availability hurts – Ex: Store 5 copies of data on different nodes – When someone goes away, you must replicate the data they held – Hard drives are *huge*, but cable modem upload bandwidth is tiny - perhaps 10 Gbytes/day – Takes many days to upload contents of 200GB hard drive. Very expensive leave/replication situation! 36 Research Trends: A Superficial History Based on Articles in IPTPS • In the early ‘00s (2002-2004): – DHT-related applications, optimizations, reevaluations… (more than 50% of IPTPS papers!) – System characterization – Anonymization • 2005-… – BitTorrent: improvements, alternatives, gaming it – Security, incentives • More recently: – Live streaming – P2P TV (IPTV) – Games over P2P 37 What’s Missing? • Very important lessons learned – …but did we move beyond vertically-integrated applications? • Can we distribute complex services on top of p2p overlays? 38 P2P: Summary • Many different styles; remember pros and cons of each – centralized, flooding, swarming, unstructured and structured routing • Lessons learned: – – – – – – – 39 Single points of failure are very bad Flooding messages to everyone is bad Underlying network topology is important Not all nodes are equal Need incentives to discourage freeloading Privacy and security are important Structure can provide theoretical bounds and guarantees