Download Mija`s presentation on new measures of data utility

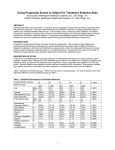
New Measures of Data Utility
Mi-Ja Woo
National Institute of Statistical Sciences
Question
How to evaluate the characteristics of SDL methods?

Previously, data utility measures were studied in
context of moments and linear regression models.
- Differences in inferences obtained from the
original and masked data.
- Regression model and KL distance rely on the
multivariate normality assumption.

Questions :
- Is the assumption satisfied in the realistic situation?
- What if the assumption is violated?
Example

Example: Two-dimensional original data and two
masked data by synthetic and resampling methods.


Different distributions, but the same moments and estimates
of regression coefficients.
New measures are needed.
1. CDF utility measure

Extension of univariate case.
Kolmogorov statistics

Cramer-von Mises statistics

, where
are empiricaldistributions of original and masked
data. Large MD and MCM indicate two data are distributed
differently.
2. Cluster Data Utility



A loose definition of clustering could be “the process of
organizing objects into groups whose members are similar
in some way”.
A cluster is therefore a collection of objects which are
“similar” between them and are “dissimilar” to the objects
belonging to other clusters.
A data set is said to be randomly assigned when proportion
of observations from original data for each cluster is
constant (1/2 with equal number of observations for two
groups) :
where
is the total number of records,
is the number
of records from original data, and
is the weight
assigned to i-th cluster.
3. Propensity Score Data Utility



A propensity score is generally defined as the
conditional probability of assignment to a particular
treatment given a vector of observed covariates
(Rosenbaum and Rubin 1983).
A data set is said to be randomly assigned when
propensity score for each covariate is constant (1/2
with equal number of observations for two groups).
In the propensity score method, a propensity score is
estimated for each observed covariate,
and
utility is measured by:
Estimation of propensity scores:


Combine original and masked data sets, and create an
indicator variable Rj with the value 0 for observations from
original and 1 otherwise.
1) Logistic regression model such as
where
2) Tree model.
3) Modified logistic regression model
: Classify all data points into g groups, and fit a logistic
model for each group. It combines logistic model with
clustering, and it borrows strength of logistics model and
clustering method.
Cluster utility is one way of propensity score utility.
4. Simulation




Eight different types of two-dimensional data with n=10,000:
1) Symmetric/non-symmetric
2) High/ low correlated
3) Negative/ positive correlated.
Masking strategies considered:
Synthetic, microaggregation, microaggregation followed by
noise, rank swapping, and resampling.
Computational details:
1) Cluster Utility: g=500 (5%) and g=1,000 (10%).
2) Propensity score utility with logistic model:
3) Propensity score utility with tree model:
Sizes of tree considered are complexity parameter cp=0.001,
and 0.0001. That is, any split that does not decrease the
overall lack of fit by a factor of cp is not attempted.
4) Propensity score utility with modified logistic model:
The number of group is g=100 (1%), and linear and
quadratic logistic functions are used to fit logistic regression
models.
Results:
Symmetric high negative case.
Symmetric low negative case.
Non-symmetric high negative case.
Non-symmetric low negative case.
Summary:


CDF utility:
1) Do not involve parameters.
2) It is favorable to rank swapping SDL method.
Cluster utility:
1) Do not measure the differences between two
structures of original and masked data within a cluster,
within-cluster variation.
2) Generally, it is consistent to overall results.
3) For non-symmetric cases, large number of clusters
tend to produce worse utility for the masked data by
microaggregation method since there are three overlaps
in microaggregated data.



Propensity score with logistic model:
1) The choice of degree is very crucial.
2) It is hard to deal with high-dimensional data.
Propensity score with tree model:
1) Small size of tree can not distinguish utility of Rank from
that of Resample.
2) Large size of tree leads to bad utility for the microaggregation method. For some cases, large size of tree can not
partition space for Rank method.
3) It is favorable to Rank SDL method.
Propensity score with modified logistic model:
1) It possesses both advantages and disadvantages of logistic
model and clustering since it is the combination of cluster and
propensity score utilities.
2) It looks consistent to overall results for all data structures.
END