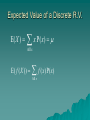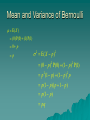* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download Chapter 5 - Dr. Dwight Galster
Indeterminism wikipedia , lookup
Random variable wikipedia , lookup
Infinite monkey theorem wikipedia , lookup
Birthday problem wikipedia , lookup
Inductive probability wikipedia , lookup
Risk aversion (psychology) wikipedia , lookup
Conditioning (probability) wikipedia , lookup
Probability interpretations wikipedia , lookup
Chapter 5
Discrete Probability
Distributions
Roll Two Dice and Record the Sums
Physical Outcome:
An ordered pair of
two faces showing.
We assign a
numeric value to
each pair by
counting up all of
the dots that show.
A Function of Events
Note that there may be
several outcomes that
get the same value.
This assignment of a
numeric value is, in fact,
a function.
The domain is a set
containing the possible
outcomes, and the range
is the set of numbers
that are assigned to the
outcomes.
You might say, for example,
f(
)=5.
Random Variable
However, we don’t use f(x) notation in this case.
This function is called a random variable and is
typically given a capital letter name, such as X.
Even though it is truly a function, we use it much
the same way that we would a variable in algebra,
except for one thing:
The random variable takes on different values
according to a probability distribution associated
with the underlying events.
That is, we can never be certain what the value
will be (random) and
The values vary (variable) from trial to trial.
The Probabilities of X
We have already used the notation P(A) in
connection with the probabilities of events.
P is a function that relates an event to a probability
(a number between 0 and 1).
Similarly, we will use expressions like P(X=x)=.5,
or P(X=3)=.5.
Why not just say P(3)=.5? We sometimes do, for
short. Technically, 3 doesn’t have a probability.
It’s the event, X=3, that has a probability.
X=3 should be understood as “X takes the value 3”,
rather than “X equals 3”.
P(X=3)=.5 says 3 is a value of X that occurs with
probability .5.
Lower-case letters are used for particular values,
upper-case for r.v. names, as in P(X=x).
A Random
Variable X
for two dice
The table lists the
outcomes that are
mapped to each
sum, x.
Outcomes
x
n(x)
(1,1)
2
1
(2,1),(1,2)
3
2
(3,1),(2,2),(1,3)
4
3
(4,1),(3,2),(2,3),(1,4)
5
4
(5,1),(4,2),(3,3),(2.4),(1,5)
6
5
(6,1),(5,2),(4,3),(3,4),(2,5),(1,6) 7
6
8
5
9
4
The n(x) column tells
how many equally
(6,2),(5,3),(4,4),(3,5),(2,6)
likely outcomes are
(6,3),(5,4),(4,5),(3,6)
in each group.
P(X=x) = n(x)/n(S)
= n(x)/36.
(6,4),(5,5),(4,6)
10 3
(6,5),(5,6)
11 2
(6,6)
12 1
Probability Histogram for X
A Probability Function Definition
A histogram is often called a “distribution” because it
graphically depicts how the probability is distributed among
the values. (Actually, a histogram is just a picture of a
distribution, not the distribution itself.)
We also like to have a formula that gives us the probability
values when this is possible.
The 2-dice toss problem gives a nice regular shape. Can
we come up with a formula for the probabilities?
It is a V-shaped function, which is typical of absolute value
graphs. Since the vertex is at x=7, we could try something
with |x-7|. A little experimentation will lead to
6 | x 7 |
if x {2,3, 4,...,12}
P( X x)
36
0
otherwise
Even Easier
Consider the toss of a single die.
– Define a random variable X as the number of spots that
show on the top face.
– Define a probability function for X as
1
if x {1, 2,3, 4,5, 6}
P( X x) 6
0
otherwise
0 if the outcome is tails
Consider a coin toss. Let X
1 if the outcome is heads
Define a probability function for X as
1
if x {0,1}
P( X x) 2
0 otherwise
Measures of Central Tendency
Find
the mean of a distribution
Think: What is a mean?
– Average of all observations
– Theoretical long run average of
observations
Calculate
this from the information in
the probability distribution
Example of a Simple Probability Distribution
Say
we have a discrete r.v. X as
follows:
x
1
2
P(X=x)
.3
.4
3
.3
Suppose
we have 10 realizations of X.
If the 10 occurred in the exact longrun proportions, what would they be?
1, 1, 1, 2, 2, 2, 2, 3, 3, 3.
Calculate the Mean
What then would the mean be?
(1 1 1 2 2 2 2 3 3 3) /10
1 3 2 4 3 3
10
10
10
1 .3 2 .4 3 .3 2
1 P(1) 2 P(2) 3 P(3)
x P( x)
All x
Note: The mean doesn’t have to be a value
of X.
Expected Value of a Discrete R.V.
E( X )
x P( x)
All x
E( f ( X ))
f ( x) P( x)
All x
Variance of a Discrete R.V.
Variance
is also an expected value
var( X ) 2 E[( X ) 2 ]
[ x P( x)]
2
Standard
2
(
x
)
P( x)
All x
2
Deviation, as always, is the
square root of the variance.
2
Example: The number of standby passengers who get
seats on a daily commuter flight from Boston to New
York is a random variable, X, with probability distribution
given below. Find the mean, variance, and standard
deviation.
x
0
1
2
3
4
5
Totals
P( x )
0.30
0.25
0.20
0.15
0.05
0.05
1.00
xP( x )
0.00
0.25
0.40
0.45
0.20
0.25
1.55
x 2 x 2 P( x )
0
0.00
1
0.25
4
0.80
9
1.35
16
0.80
25
1.25
4.45
Solution:
Using the formulas for mean, variance, and standard
deviation:
[ xP( x )] 155
.
Note: 1.55 is not a value of the random variable (in this
case). It is only what happens on average.
2 [ x 2 P( x)] 2
4.45 (1.55) 2 4.45 2.4025 2.0475
2 2.0475 143
.
Example: The probability distribution for a random
variable x is given by the probability function
8 x
P( x )
15
for
x 3, 4, 5, 6, 7
Find the mean, variance, and standard deviation.
Solution:
Find the probability associated with each value by using
the probability function.
83 5
P(3)
15 15
P(6)
86 2
15 15
84 4
P(4)
15 15
P(7)
87 1
15
15
85 3
P(5)
15 15
x
3
4
5
6
7
Totals
P( x )
5/15
4/15
3/15
2/15
1/15
15/15
xP( x )
15/15
16/15
15/15
12/15
7/15
65/15
65
[ xP( x )] 4.33
15
2
305 65
2
2
2
[ x P( x)]
1.56
15 15
2 156
. 125
.
x2
9
16
25
36
49
x 2 P( x )
45/15
64/15
75/15
72/15
49/15
305/15
Binary Experiments
(Bernoulli Trials)
A Bernoulli Trial is an experiment for which
there are only two possible outcomes.
For probability theory purposes, these are
designated “success” and “failure,”
although the names are arbitrary.
Examples include a coin toss with
outcomes of heads or tails, or any
experiment where the results are yes or
no, true or false, good or defective, etc.
The Bernoulli Distribution
A Bernoulli R.V. assigns to each outcome of a
Bernoulli Trial a 1 for success or a 0 for failure.
P(1) is denoted by p and is the parameter of the
distribution (probability of a success).
P(0)=(1–p) because {0} is the complement of {1}.
The notation q=(1-p) is also used to simplify
formulas. However, q is not another parameter,
because its value is determined by p.
Mean and Variance of Bernoulli
E( X )
(0) P(0) (1) P(1)
0 p
p
2 E( X p ) 2
(0 p ) 2 P(0) (1 p) 2 P(1)
p 2 (1 p ) (1 p ) 2 p
p (1 p )( p 1 p )
p (1 p )
pq
Some Examples
Bernoulli Trials p=0.5
1
0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
13
14
15
16
17
18
19
20
Bernoulli Trials p=0.25
1
0
1
2
3
4
5
6
7
8
9
10
11
12
Binomial Distribution
Suppose in a series of n Bernoulli Trials you
keep track of the total number of successes.
The trials are independent.
We say p and n are the parameters of the
distribution.
Let X be a r.v. for the number of successes.
Let’s start with n=2 and p is 1/4.
The next slide shows the outcomes with
corresponding values of X and probabilities.
Binomial Probability Example
Outcome
(SS)
(SF)
(FS)
(FF)
Value of X
2
1
0
Probability
(1/4)(1/4)=1/16
(1/4)(3/4)=3/16
(3/4)(1/4)=3/16
(3/4)(3/4)=9/16
Probability of
1/16
6/16
9/16
Value of X
2
1
1
0
Mean and Variance of Binomial
when n=2
E( X )
0 P(0) 1 P(1) 2 P(2)
9
6
1
0
1 2
16
16
16
8 1
np
16 2
2 E( X ) 2
2
2
2
1
1
1
0 P(0) 1 P(1) 2 P(2)
2
2
2
1 9 1 6 9 1
4 16 4 16 4 16
24 3
npq
64 8
Factorials and Combinations
n-factorial is defined as follows:
n ! n(n 1)(n 2)...(2)(1)
e.g. 6! 6 5 4 3 2 1
0! 1 by definition
n
A combination is read “n choose r” and
r
represents the number of ways to choose
r objects from n without regard to order. It
can also be written as nCr (often on
calculators). It is defined as follows:
n
n!
r r !(n r )!
Binomial Probabilities
For
a binomial r.v. X, with probability
parameter p and n trials,
n x
P( x) p (1 p) n x
x
Example: Calculate the probability
of 3 successes in 5 trials if p=.25.
5 1 3
P(3)
3 4 4
5! 9 5 4 3 2 9
45
5
4
3!2! 4
3 2 2 4 4 128
3
2
A Fishing Trip
Dr. A is fond of fly-fishing in the Colorado mountain
streams. His long-run average is one catch per 20 casts.
On the last day of his vacation, He stops to eat supper.
He figures he will cast 10 more times and then pack up.
What is the probability he will catch one more fish?
10
1
9
9
P( X 1) .05 .95 10 .05.95 .315
1
What is the probability he will catch at least one more fish?
10
0
10
10
P( X 1) 1 P( X 0) 1 .05 .95 1 .95 .401
0
What is the probability he will catch more than one fish?
P( X 1) P( X 1) P( X 1) .401 .315 .086
From Binomial to Poisson
The Binomial Distribution deals with counting
“successes” in a fixed number of trials. It is
discrete and finite-valued.
Suppose there is no specified number of trials.
We may want to count the number of “successes”
that occur in an interval of time or space.
“Successes,” or sometimes “events,” (not to be
confused with probability events) refer to
whatever we are interested in counting, such as
–
–
–
–
the number of errors on a typed page,
the number of flights that leave an airport in an hour,
the number of people who get on the bus at each stop,
or the number of flaws on the surface of a metal sheet.
Poisson Distribution
A
Poisson Random Variable, X, takes
on values 0, 1, 2, 3, . . . , corresponding
to the number of events that occur.
Since no definite upper bound can be
given, X is an infinitely-valued discrete
random variable.
Assumptions:
– The probability that an event occurs is the
same for each unit of time or space.
– The number of events that occur in one
unit of time or space is independent of any
others.
Poisson Probability Function
The
probability of observing
exactly x events or successes in a
unit of time or space is given by
x e
P( x)
x! .
μ is the mean number of
occurrences per unit time or
space, that is, E( X ).
In a most amazing coincidence, it
2
turns out that !
A Fishing Trip Too
Dr. A is fond of fly-fishing in the Colorado
mountain streams. His long-run average is
one catch per hour. On the last day of his
vacation, he stops to eat supper. He figures
he will fish two more hours and then pack up.
What is the probability he will catch at least
one more fish?
Note: μ = 2 (in a two hour period).
P(at least one) 1 P(0)
20 e 2
1
0!
2
1 e .865
More Poisson Fishing
What is the probability Dr. A will catch one more
fish?
21 e2
P(1)
2e2 .271
1!
What is the probability Dr. A will catch more than
one more fish?
P( X 1) P( X 1) P( X 1) .865 .271 .594
Discrete Distributions
The examples we have just seen are
common discrete distributions,
That is, the r.v. in question takes only
discrete values (with P>0).
We have also seen that discrete r.v.’s may
be finite or infinite with regard to the
number of values they can take (with
P>0).
There are many more such discrete
distributions, and we should mention
some of them just so you are aware they
are available.
The multinomial distribution is like the binomial,
except that it has more than two categories with
probabilities for each. The r.v. is not based on a
single value but a vector giving the counts of
each possible outcome. The counts have to add
up to the number of trials. You could use this, for
example, to calculate the probability of getting 2
fives and 2 sixes in 4 tosses of a die, written as
P(0,0,0,0,2,2).
n!
x1
x2
P( x1 , x2 ,..., xk )
p1 p2
x1! x2!
xk !
0
0
pk
0
xk
0
2
4!
1 1 1 1 1 1
P(0,0,0,0, 2, 2)
0!0!0!0!2!2! 6 6 6 6 6 6
4
3
1
1 1
6
6 6 216
2
The geometric distribution is used when you are
interested in the number of trials until the first
success. This is an infinite-valued distribution like
Poisson. You could use this, for example, to
calculate the probability that you find the first
defective on the 10th trial, if the probability of a
defective is .1.
P( x) pq x 1 where q (1 p)
P(10) (.1)(.9)9 .039
More often, we are interested in the cumulative
probability (finding the first defective by the 10th
trial):
P( X x) 1 q x
P( X 10) 1 .910 .65
The negative binomial distribution is an extension
of the geometric. Instead of counting the
number of trials until the first success, we count
the number of failures, X, until we have r
successes. For example, find the probability that
you have to examine 10 items to find 3
defectives, if the probability of a defective is .1.
x r 1 r x
P( x, r )
p q where q (1 p)
r 1
7 3 1
3
7
P(7,3)
(.1)
(.9)
.017
3 1
More on Combinations
Combinations can be used to calculate
probabilities for many common problems
like card games.
Recall the probability definition that said
n( A)
P( A)
n( S ) .
If we can find the number of combinations
of cards that fit our definition of a
particular “hand,” and divide by the total
number of combinations of cards, we can
calculate probabilities for “hands.”
number of ways of getting hand
P(hand )
total number of hands possible
Poker Hands
First,
what is the total number of
hands possible in poker? (5-card
combinations)
52 52! 52 51 50 49 48 47!
Totalhands
5 4 3 2 47!
5 5!47!
52 5110 49 2 2,598,960
This
will be our denominator.
number of ways of getting hand
P(hand )
2,598,960
Try a Flush
To figure out the numerator, we can think in
terms of the choices that have to be made to
build the hand.
For a flush, we first have to choose 1 suit out of
4. Given the suit, we have to choose 5 cards
from the 13 in that suit.
4 13 4! 13! 4 13 12 1110 9
allflushes
5 4 3 2
1 5 1!3! 5!8!
4 13 11 9 5,148
5,148
P(anyflush)
.001981
2,598,960
Not All Flushes
However,
we have to make sure we
have mutually exclusive definitions.
Not all “flushes,” are counted as
flushes. Some are straight flushes
and royal flushes.
4
royalflushes 4
1
4 9
straightflushes 4 9 36
1 1
Final Results for Flushes
So
4
P(royalflush)
.000002
2,598,960
36
P( straightflush)
.000014
2,598,960
5,148 4 36
P( flush)
.001965
2,598,960
One Pair
To get one pair (and nothing else) we need to
select a number for the pair, then 3 other,
different numbers for the remaining cards (order
doesn’t matter). However, that is not all. We
must also select suits, two for the pair and 1 for
each of the other cards.
3
13 12 4 4 13 12 1110 4 3 43
onepairs
3 2 2
1 3 2 1
13 12 1110 64 1, 098, 240
1, 098, 240
P(onepair )
.422569
2,598,960
Full House
One more example: To get a full house, you
choose one number for the pair, then two suits
for it, then another number for the triple, and
three suits for it.
13 4 12 4 13 12 4 3 4
fullhouses
2
1 2 1 3
13 12 4 3 3, 744
3, 744
P( fullhouse)
.001441
2,598,960