Download What statistical analysis should I use?

What statistical analysis
should I use? Running order
Introduction
About the A data file
One sample t-test
One sample median test
Binomial test
Chi-square goodness of fit
Two independent samples t-test
Wilcoxon-Mann-Whitney test
Chi-square test (Contingency table)
Phi coefficient
Fisher's exact test
One-way ANOVA
Kruskal Wallis test
Paired t-test
Wilcoxon signed rank sum test
Sign test
McNemar test
Cochran’s Q
About the B data file
One-way repeated measures ANOVA
Bonferroni for pairwise comparisons
About the C data file
Repeated measures logistic regression
Factorial ANOVA
Friedman test
Reshaping data
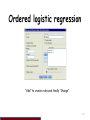
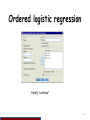
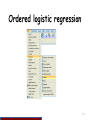
Ordered logistic regression
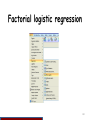
Factorial logistic regression
Correlation
Simple linear regression
Non-parametric correlation
Simple logistic regression
Multiple regression
Analysis of covariance
Multiple logistic regression
Discriminant analysis
One-way MANOVA
Multivariate multiple regression
Canonical correlation
Factor analysis
Normal probability plot
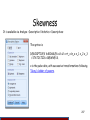
Skewness
Kurtosis
Tukey's ladder of powers
Median split
Likert Scale
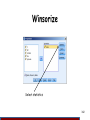
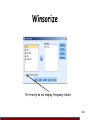
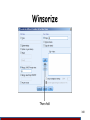
Winsorize
General Linear Models
Centre Data
Correlation - Comparison
Sobel Test
Structural Equation Modelling
Quartiles
Epilogue
PSY3029
PSY8058
1
Thursday, 25 May 2017
1:26 AM
About the A data file
About the B data file
About the C data file
Analysis of covariance
Binomial test
Bonferroni for pairwise comparisons
Canonical correlation
Centre Data
Chi-square goodness of fit
Chi-square test (Contingency table)
Cochran’s Q
Correlation
Correlation - Comparison
Discriminant analysis
Epilogue
Factor analysis
Factorial ANOVA
Factorial logistic regression
Fisher's exact test
Friedman test
General Linear Models
Introduction
Kruskal Wallis test
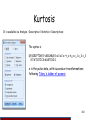
Kurtosis
Likert Scale
Linear regression
Logistic regression
McNemar test
Median split
Multiple logistic regression
Multiple regression
Multivariate multiple regression
Non-parametric correlation
Normal probability plot
One sample median test
One sample t-test
One-way ANOVA
One-way MANOVA
One-way repeated measures ANOVA
Ordered logistic regression
Paired t-test
Phi coefficient
Quartiles
Repeated measures logistic regression
Reshaping data
Sign test
Simple linear regression
Simple logistic regression
Skewness
Sobel Test
Structural Equation Modelling
Tukey's ladder of powers
Two independent samples t-test
Wilcoxon signed rank sum test
Wilcoxon-Mann-Whitney test
Winsorize
PSY3029
PSY8058
2
PSY3029
Lecture 1
Lecture 2
Lecture 3
Lecture 4
3
Thursday, 25 May 2017
1:26 AM
PSY8058
Lecture 1
Lecture 2
Lecture 3
Lecture 4
4
Thursday, 25 May 2017
1:26 AM
Introduction
For a useful general guide see Policy: Twenty tips for
interpreting scientific claims : Nature News & Comment William
J. Sutherland, David Spiegelhalter and Mark Burgman Nature
503 335–337 2013.
Some criticism has been made of their discussion of p values,
see Replication, statistical consistency, and publication bias G.
Francis, Journal of Mathematical Psychology 57(5) 153–169 2013.
Index End
5
Introduction
These examples are loosely based on a UCLA tutorial sheet. All
can be realised via the syntax window. Appropriate command
strokes are also indicated. The guidelines to the APA reporting
style is motivated by Using SPSS for Windows and Macintosh:
Analyzing And Understanding Data Samuel B. Green and Neil J.
Salkind. Much information is available on the web on the APA
style. The source text is Publication Manual of the American
Psychological Association, Sixth Edition a useful summary is
Reporting Statistics in APA Style.
These pages show how to perform a number of statistical tests
using SPSS. Each section gives a brief description of the aim of
the statistical test, when it is used, an example showing the
SPSS commands and SPSS (often abbreviated) output with a
brief interpretation of the output.
Index End
6
About the A data file
Most of the examples in this document will use a data file called A, high
school and beyond. This data file contains 200 observations from a
sample of high school students with demographic information about the
students, such as their gender (female), socio-economic status (ses) and
ethnic background (race). It also contains a number of scores on
standardized tests, including tests of reading (read), writing (write),
mathematics (math) and social studies (socst).
7
About the A data file
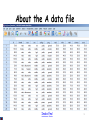
Syntax:display dictionary
/VARIABLES id female race ses schtyp prog read write math science socst.
Variable
id
Position
1
Label
female
2
race
3
ses
4
schtyp
5
type of school
prog
6
type of program
read
write
math
science
socst
7
8
9
10
11
reading score
writing score
math score
science score
social studies score
Value
Label
.00
1.00
1.00
2.00
3.00
4.00
1.00
2.00
3.00
1.00
Male
Female
Hispanic
Asian
african-amer
White
Low
Middle
High
Public
2.00
private
1.00
2.00
3.00
general
academic
vocation
8
About the A data file
Index End
9
One sample t-test
A one sample t-test allows us to test whether a sample mean (of a
normally distributed interval variable) significantly differs from a
hypothesized value. For example, using the A data file, say we wish to
test whether the average writing score (write) differs significantly
from 50. Test variable writing score (write), Test value 50. We can do
this as shown below.
Menu selection:- Analyze > Compare Means > One-Sample T test
Syntax:-
t-test
/testval = 50
/variable = write.
10
One sample t-test
Note the test value of 50 has been selected
11
One sample t-test
One-Sample Statistics
N
writing score
Mean
200
Std. Deviation
52.7750
9.47859
Std. Error Mean
.67024
One-Sample Test
Test Value = 50
Mean
t
writing score
df
4.140
Sig. (2-tailed)
199
.000
One-Sample Test
Test Value = 50
95% Confidence Interval of the
Difference
Lower
writing score
1.4533
Upper
4.0967
Difference
2.77500
The mean of the variable write
for this particular sample of
students is 52.775, which is
statistically significantly (p<.001)
different from the test value of
50. We would conclude that this
group of students has a
significantly higher mean on the
writing test than 50. This is
consistent with the reported
confidence interval (1.45,4.10)
that is (51.45,54.10) which
excludes 50, of course the midpoint is the mean.
Confidence interval
Crichton, N.
Journal Of Clinical Nursing 8(5) 618-618 1999
12
One sample t-test
Effect Size Statistics
SPSS supplies all the information necessary to compute an effect size, d,
given by:
d = Mean Difference / SD
where the mean difference and standard deviation are reported in the SPSS
output. We can also compute d from the t value by using the equation
d
t
N
where N is the total sample size. d evaluates the degree that the mean on
the test variable differs from the test value in standard deviation units.
Potentially, d can range in value from negative infinity to positive infinity. If
d equals 0, the mean of the scores is equal to the test value. As d deviates
from 0, we interpret the effect size to be stronger. What is a small versus a
large d is dependent on the area of investigation. However, d values of .2, .5
and .8, regardless of sign, are by convention interpreted as small, medium,
and large effect sizes, respectively.
13
One sample t-test
An APA Results Section
A one-sample t test was conducted to evaluate whether the mean of the
writing scores was significantly different from 50, the accepted mean. The
sample mean of 52.78 ( SD = 9.48) was significantly different from 50,
t(199) = 4.14, p < .001. The 95% confidence interval for the writing scores
mean ranged from 51.45 to 54.10. The effect size d of .29 indicates a
medium effect.
Index End
14
One sample median test
A one sample median test allows us to test whether a sample median
differs significantly from a hypothesized value. We will use the same
variable, write, as we did in the one sample t-test example above. But
we do not need to assume that it is interval and normally distributed
(we only need to assume that write is an ordinal variable).
Menu selection:- Analyze > Nonparametric Tests > One Sample
Syntax:-
nptests
/onesample test (write) wilcoxon(testvalue = 50).
15
One sample median test
16
One sample median test
Choose customize analysis
17
One sample median test
Only retain writing score
18
One sample median test
Choose tests tick “compare median…” and enter 50 as the desired
value.
Finally select the “run” button
19
One sample median test
We would conclude that this group of students has a significantly
higher median (calculated median 54) on the writing test than 50.
Index End
20
Binomial test
A one sample binomial test allows us to test whether the proportion of
successes on a two-level categorical dependent variable significantly
differs from a hypothesized value. For example, using the A data file, say
we wish to test whether the proportion of females (female) differs
significantly from 50%, i.e., from .5. We can do this as shown below.
Two alternate approaches are available.
Either
Menu selection:- Analyze > Nonparametric Tests > One Sample
Syntax:-
npar tests
/binomial (.5) = female.
Two-sided confidence intervals for the single proportion: Comparison of seven methods
Newcombe, R.G.
Statistics In Medicine 1998 17(8) 857-872
DOI: 10.1002/(SICI)1097-0258(19980430)17:8<857::AID-SIM777>3.0.CO;2-E
21
Binomial test
22
Binomial test
Choose customize analysis
23
Binomial test
Only retain female
24
Binomial test
Choose tests tick “compare observed…” and under options
25
Binomial test
enter .5 as the desired value.
Finally select the “run” button
26
Binomial test
Or
Menu selection:- Analyze > Nonparametric Tests > Legacy Dialogs > Binomial
Syntax:-
npar tests
/binomial (.5) = female.
27
Binomial test
Select female as the test variable, the default test proportion is .5
Finally select the “OK” button
28
Binomial test
Category
female Group 1 Male
Group 2 Female
Total
Binomial Test
Observed
Prop.
N
Test Prop.
91
.46
.50
109
.54
200
1.00
Exact Sig.
(2-tailed)
.229
The results indicate that there is no statistically significant difference
(p = 0.229). In other words, the proportion of females in this sample
does not significantly differ from the hypothesized value of 50%.
29
Binomial test
An APA Results Section
We hypothesized that the proportion of females is 50%. A two-tailed,
binomial test was conducted to assess this research hypothesis. The
observed proportion of .46 did not differ significantly from the
hypothesized value of .50, two-tailed p = .23. Our results suggest that
the proportion of females do not differ dramatically from males.
Index End
30
Chi-square goodness of fit
A chi-square goodness of fit test allows us to test whether the observed
proportions for a categorical variable differ from hypothesized
proportions. For example, let's suppose that we believe that the general
population consists of 10% Hispanic, 10% Asian, 10% African American
and 70% White folks. We want to test whether the observed
proportions from our sample differ significantly from these
hypothesized proportions. Note this example employs input data
(10, 10, 10, 70), in addition to A.
Menu selection:- At present the drop down menu’s cannot provide this
analysis.
Syntax:-
npar test
/chisquare = race
/expected = 10 10 10 70.
31
Chi-square goodness of fit
race
Observed Expected
N
N
hispanic
asian
africanamer
white
Total
24
11
20
145
200
Residual
20.0
4.0
20.0
-9.0
20.0
.0
140.0
5.0
Test Statistics
race
Chi-Square
df
Asymp.
Sig.
These results show that racial
composition in our sample does not
differ significantly from the
hypothesized values that we
supplied (chi-square with three
degrees of freedom = 5.029,
p = 0.170).
5.029a
3
.170
a. 0 cells (.0%) have expected frequencies less
than 5. The minimum expected cell frequency is
20.0.
Index End
32
Two independent samples
t-test
An independent samples t-test is used when you want to compare the
means of a normally distributed interval dependent variable for two
independent groups. For example, using the A data file, say we wish to
test whether the mean for write is the same for males and females.
Menu selection:- Analyze > Compare Means > Independent Samples T test
Syntax:-
t-test groups = female(0 1)
/variables = write.
33
Two independent samples
t-test
34
Two independent samples
t-test
35
Two independent samples
t-test
Do not forget to define those “pesky” groups.
36
Levene's test
In statistics, Levene's test is an inferential statistic used to assess the
equality of variances in different samples. Some common statistical
procedures assume that variances of the populations from which different
samples are drawn are equal. Levene's test assesses this assumption. It tests
the null hypothesis that the population variances are equal (called homogeneity
of variance or homoscedasticity). If the resulting p-value of Levene's test is
less than some critical value (typically 0.05), the obtained differences in
sample variances are unlikely to have occurred based on random sampling from
a population with equal variances. Thus, the null hypothesis of equal variances
is rejected and it is concluded that there is a difference between the
variances in the population.
Levene, Howard (1960). "Robust tests for equality of variances". In Ingram
Olkin, Harold Hotelling, et al. Stanford University Press. pp. 278–292.
37
Two independent samples
t-test
Group Statistics
female
writing score
male
female
N
Mean
Std. Deviation
Because the standard deviations for
the two groups are not similar (10.3 and
8.1), we will use the "equal variances
not assumed" test. This is supported by
the Levene’s test p = .001).
Std. Error Mean
91
50.1209
10.30516
1.08027
109
54.9908
8.13372
.77907
Independent Samples Test
Levene's Test for Equality of
Variances
F
writing score
Equal variances assumed
Sig.
11.133
.001
Equal variances not
assumed
Independent Samples Test
t-test for Equality of Means
Mean
t
writing score
df
Sig. (2-tailed)
Difference
Equal variances assumed
-3.734
198
.000
-4.86995
Equal variances not
-3.656
169.707
.000
-4.86995
assumed
Independent Samples Test
t-test for Equality of Means
95% Confidence Interval of the
Difference
Std. Error
Difference
writing score
Lower
Upper
Equal variances assumed
1.30419
-7.44183
-2.29806
Equal variances not
1.33189
-7.49916
-2.24073
assumed
The results indicate that there is a
statistically significant difference
between the mean writing score for
males and females (t = -3.656,
p < .0005). In other words, females
have a statistically significantly higher
mean score on writing (54.99) than
males (50.12).
This is supported by the negative
confidence interval (male - female).
38
Two independent samples
t-test
Group Statistics
female
writing score
male
female
N
Mean
Std. Deviation
Does equality of variances matter in
this case?
Std. Error Mean
91
50.1209
10.30516
1.08027
109
54.9908
8.13372
.77907
Independent Samples Test
Levene's Test for Equality of
Variances
F
writing score
Equal variances assumed
Sig.
11.133
.001
Equal variances not
assumed
Independent Samples Test
t-test for Equality of Means
Mean
t
writing score
df
Sig. (2-tailed)
Difference
Equal variances assumed
-3.734
198
.000
-4.86995
Equal variances not
-3.656
169.707
.000
-4.86995
assumed
Independent Samples Test
t-test for Equality of Means
95% Confidence Interval of the
Difference
Std. Error
Difference
writing score
Lower
Upper
Equal variances assumed
1.30419
-7.44183
-2.29806
Equal variances not
1.33189
-7.49916
-2.24073
assumed
39
Two independent samples ttest - Effect Size Statistic
Eta square, η2 , may be computed . An η2 ranges in value from 0 to 1. It is
interpreted as the proportion of variance of the test variable that is a
function of the grouping variable. A value of 0 indicates that the
difference in the mean scores is equal to 0, whereas a value of 1 indicates
that the sample means differ, and the test scores do not differ within
each group (i.e., perfect replication). You can compute η2 with the
following equation:
2
 
t
2
t  N1  N 2  2
2
What is a small versus a large η2 is dependent on the area of investigation.
However, η2 of .01, .06, and .14 are, by convention, interpreted as small,
medium, and large effect sizes, respectively.
See below.
40
Two independent samples ttest - An APA Results Section
An independent-samples t test was conducted to evaluate the hypothesis
that the mean writing score was gender dependent. The test was
significant, t (198) = -3.656, p < .0005. Male students scored lower
(M = 50.12, SD = 10.31), on average, than females (M = 54.99, SD = 8.13).
The 95% confidence interval for the difference in means was quite wide,
ranging from -7.44 to -2.30. The eta square index indicated that 7%
(η2 = .066) of the variance of the writing score was explained by gender.
It is important that you select the t test (two independent samples or
paired t test) that employs most information about your data. See the
example.
Index End
41
Wilcoxon-Mann-Whitney
test
The Wilcoxon-Mann-Whitney test is a non-parametric analog to the
independent samples t-test and can be used when you do not assume that the
dependent variable is a normally distributed interval variable (you only assume
that the variable is at least ordinal). You will notice that the SPSS syntax for
the Wilcoxon-Mann-Whitney test is almost identical to that of the
independent samples t-test. We will use the same data file (the A data file)
and the same variables in this example as we did in the independent t-test
example above. We will not assume that write, our dependent variable, is
normally distributed.
Menu selection:- Analyze > Nonparametric Tests
> Legacy Dialogs > 2 Independent Samples
Syntax:-
npar test
/m-w = write by female(0 1).
Mann-Whitney test Crichton, N. Journal Of Clinical Nursing 2000 9(4) 583-583
42
Wilcoxon-Mann-Whitney
test
The Mann-Whitney U: A Test for Assessing Whether Two Independent
Samples Come from the Same Distribution
Nadim Nachar
Tutorials in Quantitative Methods for Psychology 2008 4(1) 13-20
It is often difficult, particularly when conducting research in psychology,
to have access to large normally distributed samples. Fortunately, there
are statistical tests to compare two independent groups that do not
require large normally distributed samples. The Mann‐Whitney U is one of
these tests. In the work, a summary of this test is presented. The
explanation of the logic underlying this test and its application are also
presented. Moreover, the forces and weaknesses of the Mann‐Whitney
U are mentioned. One major limit of the Mann‐Whitney U is that the
type-I error or alpha (α) is amplified in a situation of heteroscedasticity.
Heteroscedasticity refers to the circumstance in which the variability of a
variable is unequal across the range of values of a second variable that predicts it.43
Wilcoxon-Mann-Whitney
test
The Wilcoxon-Mann-Whitney test is sometimes used for comparing the
efficacy of two treatments in trials. It is often presented as an
alternative to a t test when the data are not normally distributed.
Where as a t test is a test of population means, the Mann-Whitney test
is commonly regarded as a test of population medians. This is not strictly
true, and treating it as such can lead to inadequate analysis of data.
Mann-Whitney test is not just a test of medians: differences in spread
can be important
Anna Hart
British Medical Journal 2001 August 18; 323(7309): 391–393.
As is always the case, it is not sufficient merely to report a p value. In
the case of the Mann-Whitney test, differences in spread may
sometimes be as important as differences in medians, and these need to
be made clear.
44
Wilcoxon-Mann-Whitney
test
45
Wilcoxon-Mann-Whitney
test
Note that Mann-Whitney has been selected.
46
Wilcoxon-Mann-Whitney
test
Do not forget to define those “pesky” groups.
47
Wilcoxon-Mann-Whitney
test
Ranks
writing
score
female
male
female
Total
N
91
109
200
Test Statisticsa
writing
score
Mann-Whitney U
3606.000
Wilcoxon W
7792.000
Z
-3.329
Asymp. Sig. (2.001
tailed)
a. Grouping Variable: female
Mean
Rank
85.63
112.92
Sum of
Ranks
7792.00
12308.00
The results suggest that there is a
statistically significant difference
between the underlying distributions
of the write scores of males and the
write scores of females (z = -3.329,
p = 0.001).
48
Wilcoxon-Mann-Whitney test
- An APA Results Section
A Wilcoxon test was conducted to evaluate whether writing score was
affected by gender. The results indicated a significant difference,
z = -3.329, p = .001. The mean of the ranks for male was 85.63, while the
mean of the ranks for female was 112.92.
Index End
49
Chi-square test
(Contingency table)
A chi-square test is used when you want to see if there is a relationship
between two categorical variables. It is equivalent to the correlation
between nominal variables.
A chi-square test is a common test for nominal (categorical) data. One
application of a chi-square test is a test for independence. In this case,
the null hypothesis is that the occurrence of the outcomes for the two
groups is equal. If your data for two groups came from the same
participants (i.e. the data were paired), you should use the McNemar's
test, while for k groups you should use Cochran’s Q test.
50
Chi-square test
(Contingency table)
In SPSS, the chisq option is used on the statistics subcommand of the
crosstabs command to obtain the test statistic and its associated
p-value. Using the A data file, let's see if there is a relationship between
the type of school attended (schtyp) and students' gender (female).
Remember that the chi-square test assumes that the expected value for
each cell is five or higher. This assumption is easily met in the examples
below. However, if this assumption is not met in your data, please see the
section on Fisher's exact test.
Two alternate approaches are available.
Either
Menu selection:- Analyze > Tables > Custom Tables
Syntax:-
crosstabs
/tables = schtyp by female
/statistic = chisq phi.
51
Chi-square test
52
Chi-square test
Drag selected variables to the row/column boxes
53
Chi-square test
Select
chi-squared
Alternately
54
Chi-square test
Menu selection:- Analyze > Descriptive Statistics > Crosstabs
Syntax:-
crosstabs
/tables = schtyp by female
/statistic = chisq.
55
Chi-square test
Select row and column variables.
56
Chi-square test
Select Chi-square and Cramér’s V
Cramér's V (sometimes called phi, see below) is a measure of association between two
nominal variables, giving a value between 0 and +1 (inclusive). It is based on Pearson's
chi-squared statistic
Cramér, Harald. 1946. Mathematical Methods of Statistics. Princeton: Princeton University Press, p282. ISBN 0-69157
08004-6
Chi-square test
Case Processing Summary
Cases
type of school *
female
Valid
N
Percent
200 100.0%
N
Missing
Percent
0
.0%
Total
N
Percent
200 100.0%
type of school * female Crosstabulation
Count
Female
Total
Male
female
type of
school
Total
public
private
77
14
91
91
18
109
168
32
200
Chi-Square Tests
Asymp. Sig.
Value
Df
(2-sided)
.047a
1
.828
.001
1
.981
.047
1
.828
Exact Sig.
(2-sided)
Exact Sig.
(1-sided)
Pearson Chi-Square
Continuity Correctionb
Likelihood Ratio
Fisher's Exact Test
.849
.492
Linear-by-Linear
.047
1
.829
Association
N of Valid Cases
200
a. 0 cells (.0%) have expected count less than 5. The minimum expected count is 14.56.
b. Computed only for a 2x2 table
These results indicate
that there is no
statistically significant
relationship between the
type of school attended
and gender (chi-square
with one degree of
freedom = 0.047,
p = 0.828).
Note 0 cells have
expected count less than
5. If not use Fisher's
exact test.
58
Chi-square test
An APA Results Section
Symmetric Measures
Value
Approx. Sig.
Phi
.015
.828
Cramer's V
.015
.828
Nominal by Nominal
N of Valid Cases
200
A two-way contingency table analysis was conducted to evaluate
whether type of school exhibited a gender bias. School and gender
were found to not be significantly related, Pearson χ2 (1, N = 200) =
.047, p = .828, Cramér’s V = .015. The proportions of males were .85
and females .84.
59
Chi-square test
By adding “/CELLS=COUNT EXPECTED” or selecting
“Cells” from the Crosstabs display you can produce
the expected cells assuming independence. As
required these values exceed 5.
60
Chi-square test
Let's look at another example, this time looking at the relationship
between gender (female) and socio-economic status (ses). The point of
this example is that one (or both) variables may have more than two
levels, and that the variables do not have to have the same number of
levels. In this example, female has two levels (male and female) and ses
has three levels (low, medium and high).
Menu selection:- Analyze > Tables > Custom Tables
Using the previous menu’s.
Syntax:-
crosstabs
/tables = female by ses
/statistic = chisq phi.
61
Chi-square test
Case Processing Summary
Cases
Valid
Missing
N
Percent
N
Percent
200 100.0%
0
.0%
female * ses
Total
N
Percent
200 100.0%
female * ses Crosstabulation
Count
ses
middle
low
female male
female
Total
15
32
47
Total
high
47
48
95
29
29
58
91
109
200
Chi-Square Tests
Value
4.577a
4.679
3.110
df
Asymp. Sig.
(2-sided)
Pearson Chi-Square
2
Likelihood Ratio
2
Linear-by-Linear
1
Association
N of Valid Cases
200
a. 0 cells (.0%) have expected count less than 5. The
minimum expected count is 21.39.
Again we find that there is no
statistically significant
relationship between the
variables (chi-square with two
degrees of freedom = 4.577,
p = 0.101).
Note the absence of Fisher’s
Exact Test!
.101
.096
.078
62
Chi-square test
An APA Results Section
Symmetric Measures
Value
Approx. Sig.
Phi
.151
.101
Cramer's V
.151
.101
Nominal by Nominal
N of Valid Cases
200
A two-way contingency table analysis was conducted to evaluate
whether gender was related to social economic status (SES).
Gender and SES were not found to be significantly related,
Pearson χ2 (2, N = 200) = 4.58, p = .101, Cramér’s V = .151. The
proportions of males in low, middle and high SES were .32, .50, and
.50, respectively.
63
Chi-square test
By adding “/CELLS=COUNT EXPECTED” or selecting
“Cells” from the Crosstabs display you can produce
the expected cells assuming independence. As
required these values exceed 5.
Index End
64
Phi coefficient
The measure of association, phi, is a measure which adjusts the chi
square statistic by the sample size. The phi coefficient is the equivalent
of the correlation between nominal variables.
It may be introduced at the same time as the Chi-square.
Select Phi
65
Case Processing Summary
Phi coefficient
Cases
Valid
N
female * ses
Missing
Percent
200
N
Total
Percent
100.0%
0
N
0.0%
Percent
200
100.0%
The p values for the tests are
identical.
female * ses Crosstabulation
Count
ses
low
Total
middle
high
male
15
47
29
91
female
32
48
29
109
47
95
58
200
female
Total
Chi-Square Tests
Value
df
Asymp. Sig. (2sided)
a
2
.101
Likelihood Ratio
4.679
2
.096
Linear-by-Linear Association
3.110
1
.078
Pearson Chi-Square
4.577
N of Valid Cases
χ2 = 4.577
2
4.577
ϕ = 0.151  

 0.151
n
200
n = 200
Sometimes ϕ2 is used as a measure of
association.
200
a. 0 cells (0.0%) have expected count less than 5. The minimum
expected count is 21.39.
Symmetric Measures
Value
Approx. Sig.
Phi
.151
.101
Cramer's V
.151
.101
Nominal by Nominal
N of Valid Cases
200
Index End
66
Fisher's exact test
The Fisher's exact test is used when you want to conduct a chi-square
test but one or more of your cells has an expected frequency of five or
less. Remember that the chi-square test assumes that each cell has an
expected frequency of five or more. Fisher's exact test has no such
assumption and can be used regardless of how small the expected
frequency is. In SPSS you can only perform a Fisher's exact test on a
2x2 table, and these results are presented by default. Please see the
results from the chi-square example above.
Analysis of a 2x2 contingency table is effectively equivalent to a test for
a comparison of two proportions.
Interval estimation for the difference between independent proportions:
comparison of eleven methods
Robert G. Newcombe
Statistics in Medicine Volume 17, Issue 8, pages 873–890, 1998
DOI: 10.1002/(SICI)1097-0258(19980430)17:8<873::AID-SIM779>3.0.CO;2-I
67
Fisher's exact test
As an illustration, a comparison of proportions for the data on the
relationship between the type of school attended (schtyp) and students'
gender (female), previously analysed using a chi-squared test p-value
0.828, Fisher’s exact test 0.849.
MTB > ptwo 109 91 91 77.
Test and CI for Two Proportions
Sample
1
2
X
91
77
N
109
91
Sample p
0.834862
0.846154
Difference = p (1) - p (2)
Estimate for difference: -0.0112915
95% CI for difference: (-0.113047, 0.0904637)
Test for difference = 0 (vs not = 0): Z = -0.22
Available in SPSS see
slide from Chi squared,
but not as a comparison
of proportions.
P-Value = 0.828
Fisher's exact test: P-Value = 0.849
68
Fisher's exact test
A simple web search should reveal specific tools developed for different
size tables. For example
Fisher's exact test for up to 6×6 tables
For the more adventurous
For those interested in more detail, plus a worked example see.
Fisher's Exact Test or Paper only
When to Use Fisher's Exact Test
Keith M. Bower
American Society for Quality, Six Sigma Forum Magazine, 2(4) 2003, 35-37.
69
Fisher's exact test
For larger examples you might try (my coding)
Fisher's Exact Test
Algorithm 643
FEXACT - A Fortran Subroutine For Fisher’s Exact Test On Unordered
R x C Contingency-Tables
Mehta, C.R. and Patel, N.R.
ACM Transactions On Mathematical Software 12(2) 154-161 1986.
A Remark On Algorithm-643 - FEXACT - An Algorithm For
Performing Fisher’s Exact Test In R x C Contingency-Tables
Clarkson, D.B., Fan, Y.A. and Joe, H.
ACM Transactions On Mathematical Software 19(4) 484-488 1993.
Index End
70
One-way ANOVA
A one-way analysis of variance (ANOVA) is used when you have a
categorical independent variable (with two or more categories). A
normally distributed interval dependent variable. You wish to test for
differences in the means of the dependent variable broken down by the
levels of the independent variable. For example, using the A data file, say
we wish to test whether the mean of write differs between the three
program types (prog). The command for this test would be:
Menu selection:- Analyze > Compare Means > One-way ANOVA
Syntax:-
oneway write by prog.
Information point: Analysis of variance (ANOVA)
Crichton, N.
Journal Of Clinical Nursing 2000 9(3) 380-380
71
One-way ANOVA
72
One-way ANOVA
73
One-way ANOVA
ANOVA
writing score
Between
Groups
Within Groups
Total
Sum of
Squares
3175.698
14703.177
17878.875
df
2
197
199
Mean
Square
1587.849
F
21.275
Sig.
.000
74.635
The mean of the dependent variable differs significantly among the
levels of program type. However, we do not know if the difference is
between only two of the levels or all three of the levels.
74
One-way ANOVA
To see the mean of write for each level of program type,
Menu selection:- Analyze > Compare Means > Means
Syntax:-
means tables = write by prog.
75
One-way ANOVA
76
One-way ANOVA
77
One-way ANOVA
Case Processing Summary
Cases
Included
N
writing score * type of
program
Excluded
Percent
200
N
100.0%
Total
Percent
0
.0%
N
200
Percent
100.0%
Report
writing score
type of
program
general
academic
vocation
Total
Mean
51.3333
56.2571
46.7600
52.7750
N
45
105
50
200
Std.
Deviation
9.39778
7.94334
9.31875
9.47859
From this we can see that the students in the academic program have
the highest mean writing score, while students in the vocational
program have the lowest. For a more detailed analysis refer to
Bonferroni for pairwise comparisons .
78
One-way ANOVA
For an effect size statistic, η2, we need to run a general linear model
using an alternate approach.
Recall: Eta square, η2, ranges in value from 0 to 1. It is interpreted as
the proportion of variance of the test variable that is a function of
the grouping variable. A value of 0 indicates that the difference in the
mean scores is equal to 0, whereas a value of 1 indicates that the
sample means differ, and the test scores do not differ within each
group (i.e., perfect replication).
Syntax
unianova write by prog
/method=sstype(3)
/intercept=include
/print=etasq
/criteria=alpha(.05)
/design=prog.
79
One-way ANOVA
80
One-way ANOVA
81
One-way ANOVA
An APA Results Section
Tests of Between-Subjects Effects
Dependent Variable: writing score
Source
Type III Sum of
df
Mean Square
F
Sig.
Squares
Partial Eta
Squared
a
2
1587.849
21.275
.000
.178
460403.797
1
460403.797
6168.704
.000
.969
prog
3175.698
2
1587.849
21.275
.000
.178
Error
14703.177
197
74.635
Total
574919.000
200
17878.875
199
Corrected Model
Intercept
Corrected Total
3175.698
a. R Squared = .178 (Adjusted R Squared = .169)
A one-way analysis of variance was conducted to evaluate the relationship
between writing score and the type of program. The independent variable,
the type of program, included three levels, general, academic and vocation.
The dependent variable was the writing score. The ANOVA was significant
at the .05 level, F (2, 197) = 21.28, p < .0005. The strength of relationship
between the writing score and the type of program, as assessed by η2
(called partial eta squared), was strong, with the writing score factor
accounting for 18% of the variance of the dependent variable.
My note!
82
Index End
Kruskal Wallis test
The Kruskal Wallis test is used when you have one independent
variable with two or more levels and an ordinal dependent variable.
In other words, it is the non-parametric version of ANOVA and a
generalized form of the Mann-Whitney test method, since it
permits two or more groups. We will use the same data file as the
one way ANOVA example above (the A data file) and the same
variables as in the example above, but we will not assume that write
is a normally distributed interval variable.
Menu selection:- Analyze > Nonparametric Tests
> Legacy Dialogs > k Independent Samples
Syntax:-
npar tests
/k-w = write by prog (1,3).
83
Kruskal Wallis test
84
Kruskal Wallis test
85
Kruskal Wallis test
Do not forget the range for those “pesky” groups.
86
Kruskal Wallis test
Ranks
type of
program
writing
score
general
academic
vocation
Total
Test Statisticsa,b
writing
score
Chi-Square
34.045
df
2
Asymp.
.000
Sig.
a. Kruskal Wallis Test
b. Grouping Variable: type of
program
N
45
105
50
200
Mean
Rank
90.64
121.56
65.14
If some of the scores receive tied
ranks, then a correction factor is
used, yielding a slightly different
value of chi-squared. With or without
ties, the results indicate that there is
a statistically significant difference
(p < .0005) among the three type of
programs.
87
Kruskal Wallis test
An APA Results Section
A Kruskal-Wallis test was conducted to evaluate differences among the
three types of program (general, academic and vocation) on median change
in the writing score). The test, which was corrected for tied ranks, was
significant, χ2 (2, n = 200) = 34.045, p < .001. The proportion of variability
in the ranked dependent variable accounted for by the type of program
variable was .17 (χ2/(n-1)), indicating a fairly strong relationship between
type of program and writing score.
My note!
Index End
88
Paired t-test
A paired (samples) t-test is used when you have two related
observations (i.e., two observations per subject) and you want to see if
the means on these two normally distributed interval variables differ
from one another. For example, using the A data file we will test
whether the mean of read is equal to the mean of write.
Often used to compare before/after treatment.
Menu selection:- Analyze > Compare Means > Paired-Samples T test
Syntax:-
t-test pairs = read with write (paired).
89
Paired t-test
90
Paired t-test
91
Paired t-test
Paired Samples Statistics
Std.
Deviation
Mean
N
Pair 1 reading score 52.2300
200
10.25294
writing score
52.7750
200
9.47859
Paired Samples Correlations
Correlatio
n
N
Pair 1 reading score &
writing score
Std. Error
Mean
.72499
200
.67024
Sig.
.000
.597
Paired Samples Test
Paired Differences
Std.
Std. Error
Mean
Deviation
Mean
Pair 1 reading score - writing
-.54500
8.88667
.62838
score
These results indicate that the mean of
read is not statistically significantly
different from the mean of write
(t = -0.867, p = 0.387).
The confidence interval includes the origin
(no difference).
Paired Samples Test
Paired Differences
95% Confidence Interval of
the Difference
Lower
Upper
Pair 1 reading score - writing
score
-1.78414
.69414
t
-.867
Paired Samples Test
df
Pair 1 reading score - writing
score
199
Sig. (2tailed)
.387
92
Paired t-test
An APA Results Section
A paired-samples t test was conducted to evaluate whether reading and
writing scores were related. The results indicated that the mean score
for writing (M = 52.78, SD = 9.48) was not significantly greater than the
mean score fro reading ( M = 52.23, SD = 10.25), t (199) = -.87, p = .39.
The standardized effect size index, d , was .06. The 95% confidence
interval for the mean difference between the two ratings was -1.78 to
.69.
Recall
d
t
N
Index End
93
Wilcoxon signed rank sum
test
The Wilcoxon signed rank sum test is the non-parametric version of a
paired samples t-test. You use the Wilcoxon signed rank sum test when
you do not wish to assume that the difference between the two variables
is interval and normally distributed (but you do assume the difference is
ordinal). We will use the same example as above, but we will not assume
that the difference between read and write is interval and normally
distributed.
Menu selection:- Analyze > Nonparametric Tests
> Legacy Dialogs > 2 Related Samples
Syntax:-
npar test
/wilcoxon = write with read (paired).
Wilcoxon signed rank test
Crichton, N.
Journal Of Clinical Nursing 9(4) 584-584 2000
94
Wilcoxon signed rank sum
test
95
Wilcoxon signed rank sum
test
Select Wilcoxon
96
Wilcoxon signed rank sum
test
Ranks
97a
Mean
Rank
95.47
Sum of
Ranks
9261.00
88b
90.27
7944.00
N
reading score - writing
score
Negative
Ranks
Positive Ranks
Ties
Total
a. reading score < writing score
b. reading score > writing score
c. reading score = writing score
Test Statisticsb
reading score
- writing
score
Z
-.903a
Asymp. Sig. (2.366
tailed)
a. Based on positive ranks.
b. Wilcoxon Signed Ranks Test
c
15
200
The results suggest that
there is not a
statistically significant
difference (p = 0.366)
between read and write.
Index End
97
Sign test
If you believe the differences between read and write were not ordinal
but could merely be classified as positive and negative, then you may
want to consider a sign test in lieu of sign rank test. The Sign test
answers the question “How Often?”, whereas other tests answer the
question “How Much?”. Again, we will use the same variables in this
example and assume that this difference is not ordinal.
Menu selection:- Analyze > Nonparametric Tests
> Legacy Dialogs > 2 Related Samples
Syntax:-
npar test
/sign = read with write (paired).
98
Sign test
99
Sign test
Select Sign
For samples that are not too large also select “Exact”
100
Sign test
Frequencies
N
writing score - reading Negative
score
Differencesa
88
Positive
Differencesb
97
Tiesc
Total
We conclude that no statistically
significant difference was found
(p = 0.556).
15
200
a. writing score < reading score
b. writing score > reading score
c. writing score = reading score
Test Statisticsa
writing score
- reading
score
Z
-.588
Asymp. Sig. (2.556
tailed)
a. Sign Test
101
Sign test
An APA Results Section
A Wilcoxon signed ranks test was conducted to evaluate whether
reading and writing scores differed. The results indicated a nonsignificant difference, z = -.59, p = .56. The mean of the negative
ranks were 95.47 and the positive were 90.27.
Index End
102
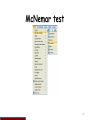
McNemar test
McNemar's test is a statistical test used on paired nominal data. It is applied to
2×2 contingency tables with a dichotomous trait, with matched pairs of
subjects, to determine whether the row and column marginal frequencies are
equal (that is, whether there is “marginal homogeneity”). For k groups use
Cochran’s Q test.
You would perform McNemar's test if you were interested in the marginal
frequencies of two binary outcomes. These binary outcomes may be the same
outcome variable on matched pairs (like a case-control study) or two outcome
variables from a single group. Continuing with the A dataset used in several
above examples, let us create two binary outcomes in our dataset: himath and
hiread. These outcomes can be considered in a two-way contingency table.
The null hypothesis is that the proportion of students in the himath group is the
same as the proportion of students in hiread group (i.e., that the contingency
table is symmetric).
Menu selection:- Transform > Compute Variable
Analyze > Descriptive Statistics > Crosstabs
The syntax is on the next slide.
103
McNemar test
Syntax:-
COMPUTE himath=math>60.
COMPUTE hiread=read>60.
EXECUTE.
CROSSTABS
/TABLES=himath BY hiread
/STATISTICS=MCNEMAR
/CELLS=COUNT.
104
McNemar test
First the transformation
105
McNemar test
Which is utilised twice, for math and read
106
McNemar test
107
McNemar test
Now the test
108
McNemar test
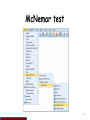
Select McNemar
109
McNemar test
Case Processing Summary
Cases
Valid
himath *
hiread
N
200
Missing
Percent
100.0%
N
0
himath * hiread Crosstabulation
Count
hiread
Total
.00
1.00
himath .00
1.00
Total
135
18
153
21
26
47
156
44
200
Percent
.0%
Total
N
Percent
200 100.0%
McNemar's chi-square
statistic suggests that
there is not a statistically
significant difference in
the proportion of students
in the himath group and
the proportion of students
in the hiread group.
Alternately accessing the
command directly.
Chi-Square Tests
Exact Sig.
Value
(2-sided)
McNemar Test
.749a
N of Valid
200
Cases
a. Binomial distribution used.
110
McNemar test
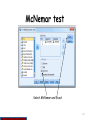
Menu selection:- Analyze > Nonparametric Tests > Legacy Dialogs
> 2 Related Samples
Syntax:-
NPAR TESTS
/MCNEMAR=himath WITH hiread (PAIRED)
/MISSING ANALYSIS
/METHOD=EXACT TIMER(5).
111
McNemar test
112
McNemar test
Select McNemar and Exact
113
McNemar test
McNemar's chi-square
statistic suggests that there
is not a statistically
significant difference in the
proportion of students in the
himath group and the
proportion of students in the
hiread group.
114
McNemar test
An APA Results Section
Proportions of student scoring high in math and reading were .22
and .24, respectively. A McNemar test, which evaluates
differences among related proportions, was not significant,
χ2 (1, n = 200) = .10, p = .75.
Index End
115
Cochran’s Q test
In the analysis of two-way randomized block designs where the response
variable can take only two possible outcomes (coded as 0 and 1), Cochran's Q
test is a non-parametric statistical test to verify whether k treatments have
identical effects. Your data for the k groups come from the same participants
(i.e. the data are paired).
You would perform Cochran’s Q test if you were interested in the marginal
frequencies of three or more binary outcomes. Continuing with the A dataset
used in several above examples, let us create three binary outcomes in our
dataset: himath, hiread and hiwrite. The null hypothesis is that the proportion
of students in each group is the same.
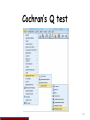
Menu selection:- Transform > Compute Variable
Analyze > Nonparametric Tests
> Legacy Dialogs > K Related Samples
The syntax is on the next slide.
116
Cochran’s Q test
Syntax:-
COMPUTE himath=math>60.
COMPUTE hiread=read>60.
COMPUTE hiwrite=write>60.
EXECUTE.
NPAR TESTS
/COCHRAN=himath hiread hiwrite
/MISSING LISTWISE
/METHOD=EXACT TIMER(5).
117
Cochran’s Q test
First transform
118
Cochran’s Q test
Which is utilised three times, for math, read and write.
Now you can perform the test.
119
Cochran’s Q test
120
Cochran’s Q test
Select Friedman, Kendall’s W and Cochran’s Q also Exact
121
Cochran’s Q test
Cochran’s Q statistic (which is a chisquared statistic) suggests that
there is not a statistically
significant difference in the
proportion of students in the
himath, hiread and hiwrite groups.
122
Cochran’s Q test
Necessary for summary
Friedman Test
Kendall's W Test
Ranks
Ranks
Mean Rank
Mean Rank
himath
1.98
himath
1.98
hiread
2.00
hiread
2.00
hiwrite
2.02
hiwrite
2.02
a
Test Statistics
Test Statistics
N
Chi-Square
df
200
N
.603
Kendall's W
2
Chi-Square
200
a
.002
.603
Asymp. Sig.
.740
df
Exact Sig.
.761
Asymp. Sig.
.740
Point Probability
.058
Exact Sig.
.761
Point Probability
.058
a. Friedman Test
2
a. Kendall's Coefficient of
Concordance
123
Cochran’s Q test
An APA Results Section
Proportions of student scoring high in math, reading and writing were
.22, .24, and .25, respectively. A Cochran test, which evaluates
differences among related proportions, was not significant,
χ2 (2, n = 200) = .60, p = .74. The Kendall coefficient of concordance
was .002.
Index End
124
Cochran’s Q test
When you find any significant effect, you need to do a post-hoc test (as
you do for ANOVA). For Cochran's Q test: run multiple McNemar's
tests and adjust the p values with the Bonferroni correction (a method
used to address the problem of multiple comparisons, over corrects for
Type I error).
Cochran, W.G. (1950). The Comparison of Percentages in Matched
Samples Biometrika, 37, 256-266.
Index End
125
About the B data file
We have an example data set called B, which is used in Roger E.
Kirk's book Experimental Design: Procedures for Behavioral
Sciences (Psychology) (ISBN 0534250920).
Suppose that I am interested in the effects of sleep
deprivation, treatment y, on hand-steadiness. The four levels
of sleep deprivation of interest are 12, 18, 24, and 30 hours,
which are denoted by y1, y2, y3, and y4, respectively. Suppose
that I have conducted an experiment in which 32 subjects
were randomly assigned to the four levels of sleep deprivation,
with the restriction that 8 subjects were assigned to each
level. The dependent variable is the number of times during a
2-minute interval that a stylus makes contact with the side of
a half-inch hole. The research hypothesis that led to the
experiment is based on the idea that sleep deprivation affects
hand steadiness.
126
About the B data file
We have an example data set called B, which is used in Roger E.
Kirk's book Experimental Design: Procedures for Behavioral
Sciences (Psychology) (ISBN 0534250920).
Syntax:-
display dictionary
/VARIABLES s y1 y2 y3 y4.
Variable
s
y1
y2
y3
y4
Position
1
2
3
4
5
Measurement Level
Ordinal
Scale
Scale
Scale
Scale
127
About the B data file
Index End
128
One-way repeated
measures ANOVA
You would perform a one-way repeated measures analysis of variance if you
had one categorical independent variable. A normally distributed interval
dependent variable that was repeated at least twice for each subject. This
is the equivalent of the paired samples t-test, but allows for two or more
levels of the categorical variable. This tests whether the mean of the
dependent variable differs by the categorical variable. In data set B, y (y1
y2 y3 y4) is the dependent variable, a is the repeated measure (a name you
assign) and s is the variable that indicates the subject number.
Menu selection:- Analyze > General Linear Model > Repeated Measures
Syntax:-
glm y1 y2 y3 y4
/wsfactor a(4).
129
One-way repeated
measures ANOVA
130
One-way repeated
measures ANOVA
You chose the factor name a which you then “Add”.
You could choose something more meaningfull.
131
One-way repeated
measures ANOVA
You chose the factor name a which you then “Add”.
132
One-way repeated
measures ANOVA
Finally
133
One-way repeated
measures ANOVA
Loads of output!!
Within-Subjects
Factors
Measure:MEASURE
_1
Dependent
Variable
a
1
y1
2
y2
3
y3
4
y4
Effect
a
Pillai's Trace
Wilks' Lambda
Hotelling's Trace
Roy's Largest
Root
a. Exact statistic
b. Design: Intercept
Within Subjects Design: a
Multivariate Testsb
Hypothesis
df
Value
F
.754
.246
5.114a
5.114a
Error df
3.000
5.000
3.000
5.000
3.068
3.068
5.114a
5.114a
3.000
3.000
.339
6.187
df
5.000
5.000
Sig.
5
.295
Sphericity
Assumed
Mean
Square
df
F
Sig.
49.000
3
16.333
11.627
.000
GreenhouseGeisser
Huynh-Feldt
Lower-bound
Error(a) Sphericity
Assumed
GreenhouseGeisser
49.000
1.859
26.365
11.627
.001
49.000
49.000
29.500
2.503
1.000
21
19.578
49.000
1.405
11.627
11.627
.000
.011
29.500
13.010
2.268
Huynh-Feldt
Lower-bound
29.500
29.500
17.520
7.000
1.684
4.214
Sig.
.055
.055
.055
.055
Type III Sum
of Squares
Source
A
Mauchly's Test of Sphericityb
Measure:MEASURE_1
Within Subjects
Mauchly's Approx. ChiEffect
W
Square
a
Tests of Within-Subjects Effects
Measure:MEASURE_1
Tests of Within-Subjects Contrasts
Measure:MEASURE_1
Type III Sum
Mean
of Squares
Square
Source a
df
A
Linear
44.100
1
44.100
Quadrati
c
Cubic
Error(a) Linear
Quadrati
c
Cubic
F
19.294
Sig.
.003
4.500
1
4.500
3.150
.119
.400
16.000
10.000
1
7
7
.400
2.286
1.429
.800
.401
3.500
7
.500
b
Mauchly's Test of Sphericity
Measure:MEASURE_1
Epsilona
Within Subjects
GreenhouseHuynhLowerEffect
Geisser
Feldt
bound
A
.620
.834
.333
Tests the null hypothesis that the error covariance matrix of the
orthonormalized transformed dependent variables is
proportional to an identity matrix.
a. May be used to adjust the degrees of freedom for the
averaged tests of significance. Corrected tests are displayed in
the Tests of Within-Subjects Effects table.
Tests of Between-Subjects Effects
Measure:MEASURE_1
Transformed Variable:Average
Type III Sum
Mean
Source
of Squares
df
Square
F
Intercep
t
Error
578.000
1
31.500
7
578.000 128.444
Sig.
.000
4.500
134
One-way repeated
measures ANOVA
Tests of Within-Subjects Effects
Measure:MEASURE_1
Source
A
Sphericity
Assumed
GreenhouseGeisser
Huynh-Feldt
Lower-bound
Error(a) Sphericity
Assumed
GreenhouseGeisser
Huynh-Feldt
Lower-bound
Type III Sum
of Squares
49.000
3
Mean
Square
16.333
F
11.627
Sig.
.000
49.000
1.859
26.365
11.627
.001
49.000
49.000
29.500
2.503
1.000
21
19.578
49.000
1.405
11.627
11.627
.000
.011
29.500
13.010
2.268
29.500
29.500
17.520
7.000
1.684
4.214
df
You will notice that this output
gives four different
p-values. The output labelled
“sphericity assumed” is the pvalue (<0.0005), that you would
get if you assumed compound
symmetry in the variancecovariance matrix. Because that
assumption is often not valid, the
three other p-values offer
various corrections (the HuynhFeldt, H-F, Greenhouse-Geisser,
G-G and Lower-bound). No matter
which p-value you use, our results
indicate that we have a
statistically significant effect of
a at the .05 level.
135
One-way repeated
measures ANOVA
An APA Results Section
A one-way within-subjects ANOVA was conducted with the factor being hand
steadiness and the dependent variable being the number hours of sleep
deprivation (y). The means and standard deviations for scores are presented
above . The results for the ANOVA indicated a significant time effect, Wilks’s
λ = .25, F (3, 21) = 11.63, p < .0005, multivariate η2 = .75 (1-λ).
My note!
Index End
136
Bonferroni for pairwise
comparisons
This is a minor extension of the
previous analysis.
Menu selection:Analyze
> General Linear Model
> Repeated Measures
Syntax:GLM y1 y2 y3 y4
/WSFACTOR=a 4 Polynomial
/METHOD=SSTYPE(3)
Only the additional outputs are
presented.
137
Bonferroni for pairwise
comparisons
Descriptive Statistics
Mean
Std. Deviation
N
3.0000
1.51186
8
3.5000
.92582
8
4.2500
1.03510
8
6.2500
2.12132
8
This table simply provides
important descriptive statistics
for the analysis as shown below.
138
Bonferroni for pairwise
comparisons
Estimated Marginal Means
a
Estimates
Measure:MEASURE_1
95% Confidence Interval
a
Mean
Std. Error
Lower Bound
Upper Bound
1
3.000
.535
1.736
4.264
2
3.500
.327
2.726
4.274
3
4.250
.366
3.385
5.115
4
6.250
.750
4.477
8.023
Using post hoc tests to examine
whether estimated marginal
means differ for levels of
specific factors in the model.
139
Bonferroni for pairwise
comparisons
Pairwise Comparisons
Measure:MEASURE_1
95% Confidence Interval for
Difference
Mean Difference
(J) a
1
2
-.500
.327
1.000
-1.690
.690
3
-1.250
.491
.230
-3.035
.535
4
-3.250
*
.726
.017
-5.889
-.611
1
.500
.327
1.000
-.690
1.690
3
-.750
.412
.668
-2.248
.748
4
-2.750
.773
.056
-5.562
.062
1
1.250
.491
.230
-.535
3.035
2
.750
.412
.668
-.748
2.248
4
-2.000
.681
.131
-4.477
.477
1
3.250
*
.726
.017
.611
5.889
2
2.750
.773
.056
-.062
5.562
3
2.000
.681
.131
-.477
4.477
3
4
Std. Error
Based on estimated marginal means
a. Adjustment for multiple comparisons: Bonferroni.
*. The mean difference is significant at the .05 level.
Sig.
a
(I) a
2
(I-J)
Lower Bound
a
Upper Bound
The results presented in the
previous Tests of Within-Subjects
Effects table, the Huynh-Feldt
(p < .0005) informed us that we
have an overall significant
difference in means, but we do not
know where those differences
occurred.
This table presents the results of
the Bonferroni post-hoc test, which
allows us to discover which specific
means differed.
Remember, if your overall ANOVA
result was not significant, you
should not examine the Pairwise
Comparisons table.
140
Bonferroni for pairwise
comparisons
Pairwise Comparisons
Measure:MEASURE_1
95% Confidence Interval for
Difference
Mean Difference
(J) a
1
2
-.500
.327
1.000
-1.690
.690
3
-1.250
.491
.230
-3.035
.535
4
-3.250
*
.726
.017
-5.889
-.611
1
.500
.327
1.000
-.690
1.690
3
-.750
.412
.668
-2.248
.748
4
-2.750
.773
.056
-5.562
.062
1
1.250
.491
.230
-.535
3.035
2
.750
.412
.668
-.748
2.248
4
-2.000
.681
.131
-4.477
.477
1
3.250
*
.726
.017
.611
5.889
2
2.750
.773
.056
-.062
5.562
3
2.000
.681
.131
-.477
4.477
3
4
Std. Error
Sig.
a
(I) a
2
(I-J)
Lower Bound
a
Upper Bound
We can see that there was a
significant difference between 1
and 4 (p = 0.017), while 2 and 4
merit further consideration.
In true SPSS style the results are
duplicated.
Based on estimated marginal means
a. Adjustment for multiple comparisons: Bonferroni.
*. The mean difference is significant at the .05 level.
141
Bonferroni for pairwise
comparisons
Multivariate Tests
Partial Eta
Value
Pillai's trace
Wilks' lambda
Hotelling's trace
Roy's largest root
.754
.246
3.068
3.068
F
Hypothesis df
Error df
Sig.
Squared
5.114
a
3.000
5.000
.055
.754
5.114
a
3.000
5.000
.055
.754
5.114
a
3.000
5.000
.055
.754
5.114
a
3.000
5.000
.055
.754
Each F tests the multivariate effect of a. These tests are based on the linearly independent pairwise comparisons
among the estimated marginal means.
a. Exact statistic
The table provides four variants of the F test. Wilks' lambda is the most
commonly reported. Usually the same substantive conclusion emerges from
any variant. For these data, we conclude that none of effects are
significant (p = 0.055). See next slide.
142
Bonferroni for pairwise
comparisons
Wilks lambda is the easiest to understand and therefore the most frequently used. It
has a good balance between power and assumptions. Wilks lambda can be interpreted as
the multivariate counterpart of a univariate R-squared, that is, it indicates the
proportion of generalized variance in the dependent variables that is accounted for by
the predictors.
Correct Use of Repeated Measures Analysis of Variance
E. Park, M. Cho and C.-S. Ki. Korean J. Lab. Med. 2009 29 1-9
Wilks' lambda performs, in the multivariate setting, with a combination of
dependent variables, the same role as the F-test performs in one-way analysis of
variance. Wilks' lambda is a direct measure of the proportion of variance in the
combination of dependent variables that is unaccounted for by the independent variable
(the grouping variable or factor). If a large proportion of the variance is accounted for
by the independent variable then it suggests that there is an effect from the grouping
variable and that the groups have different mean values.
Information Point: Wilks' lambda
Nicola Crichton Journal of Clinical Nursing, 9, 381-381, 2000.
Index End
143
About the C data file
The C data set contains 3 pulse measurements from each of 30 people
assigned to 2 different diet regiments and 3 different exercise
regiments.
Syntax:-
display dictionary
/VARIABLES id diet exertype pulse time highpulse.
Variable
id
diet
exertype
pulse
time
highpulse
Position
1
2
3
4
5
6
144
About the C data file
Index End
145
Repeated measures logistic
regression
If you have a binary outcome measured repeatedly for each subject and
you wish to run a logistic regression that accounts for the effect of
multiple measures from single subjects, you can perform a repeated
measures logistic regression. In SPSS, this can be done using the
GENLIN command and indicating binomial as the probability distribution
and logit as the link function to be used in the model. In C, if we define a
"high" pulse as being over 100, we can then predict the probability of a
high pulse using diet regime.
Menu selection:- Analyze > Generalized Estimating Equations
However see the next slide.
146
Repeated measures logistic
regression
While the drop down menu’s can be employed to set the arguments it is
simpler to employ the syntax window.
Syntax:-
GENLIN highpulse (REFERENCE=LAST)
BY diet (order=DESCENDING)
/MODEL diet
DISTRIBUTION=BINOMIAL
LINK=LOGIT
/REPEATED SUBJECT=id CORRTYPE=EXCHANGEABLE.
For completeness the drop down menu saga is shown, some 9 slides!
147
Repeated measures logistic
regression
148
Repeated measures logistic
regression
149
Repeated measures logistic
regression
150
Repeated measures logistic
regression
151
Repeated measures logistic
regression
152
Repeated measures logistic
regression
153
Repeated measures logistic
regression
154
Repeated measures logistic
regression
155
Repeated measures logistic
regression
156
Repeated measures logistic
regression
Goodness of Fitb
Model Information
Dependent Variable
highpulsea
Probability Distribution
Binomial
Link Function
Logit
Subject
1
id
Effect
Working Correlation Matrix Structure Exchangeable
a. The procedure models .00 as the response, treating 1.00 as the
reference category.
Value
Quasi Likelihood under
113.986
Independence Model
Criterion (QIC)a
Corrected Quasi Likelihood
111.340
under Independence Model
Criterion (QICC)a
Dependent Variable: highpulse
Model: (Intercept), diet
a. Computed using the full log quasi-
Case Processing Summary
N
Percent
Included
90 100.0%
Exclude
0
.0%
d
Total
90 100.0%
likelihood function.
b. Information criteria are in small-isbetter form.
Tests of Model Effects
Type III
Loads of output!!
Wald Chi-
Number of Levels
Correlated Data Summary
Subject
id
Effect
Number of Subjects
Number of
Minimum
Measurements per
Maximum
Subject
Correlation Matrix Dimension
Square
90
df
Sig.
(Intercept)
8.437
1
.004
diet
1.562
1
.211
30
3
3
Dependent Variable: highpulse
Model: (Intercept), diet
Parameter Estimates
3
Categorical Variable Information
N
Percent
Dependent
highpulse .00
63
70.0%
Variable
1.00
27
30.0%
Total
90 100.0%
Factor
diet
2.00
45
50.0%
1.00
45
50.0%
Total
Source
30
95% Wald Confidence Interval
Parameter
B
(Intercept)
1.253
.4328
.404
2.101
[diet=2.00]
-.754
.6031
-1.936
.428
[diet=1.00]
0a
.
.
.
(Scale)
1
Std. Error
Lower
Upper
100.0%
157
Repeated measures logistic
regression
Parameter Estimates
Hypothesis Test
Parameter
(Intercept)
[diet=2.00]
[diet=1.00]
(Scale)
Wald
ChiSquare
df
8.377
1.562
.
1
1
.
Sig.
.004
.211
.
Dependent Variable: highpulse
Model: (Intercept), diet
a. Set to zero because this parameter is
redundant.
These results indicate that diet is not statistically significant (Wald
Chi-Square = 1.562, p = 0.211).
Index End
158
Factorial ANOVA
A factorial ANOVA has two or more categorical independent variables
(either with or without the interactions) and a single normally distributed
interval dependent variable. For example, using the A data file we will look
at writing scores (write) as the dependent variable and gender (female)
and socio-economic status (ses) as independent variables, and we will
include an interaction of female by ses. Note that in SPSS, you do not
need to have the interaction term(s) in your data set. Rather, you can
have SPSS create it/them temporarily by placing an asterisk between the
variables that will make up the interaction term(s). For the approach
adopted here, this step is automatic. However, see the syntax example
below.
Menu selection:- Analyze > General Linear Model > Univariate
Syntax:-
glm write by female ses.
159
Factorial ANOVA
Alternate
Syntax:-
UNIANOVA write BY female ses
/METHOD=SSTYPE(3)
/INTERCEPT=INCLUDE
/CRITERIA=ALPHA(0.05)
/DESIGN=female ses female*ses.
Note the interaction term, female*ses.
160
Factorial ANOVA
161
Factorial ANOVA
162
Factorial ANOVA
Between-Subjects Factors
Value Label
female
ses
N
.00
male
91
1.00
female
1.00
low
47
2.00
middle
95
3.00
high
58
109
Tests of Between-Subjects Effects
Dependent Variable:writing score
Type III Sum of
Source
Squares
df
Mean Square
F
Sig.
2278.244a
5
455.649
5.666
.000
473967.467
1
473967.467
5893.972
.000
female
1334.493
1
1334.493
16.595
.000
ses
1063.253
2
531.626
6.611
.002
21.431
2
10.715
.133
.875
Error
15600.631
194
80.416
Total
574919.000
200
17878.875
199
Corrected Model
Intercept
female * ses
Corrected Total
a. R Squared = 0127 (Adjusted R Squared = 0105)
These results indicate that
the overall model is
statistically significant
(F = 5.666, p < 0.0005). The
variables female and ses are
also statistically significant
(F = 16.595, p < 0.0005 and
F = 6.611, p = 0.002,
respectively). However, note
that interaction between
female and ses is not
statistically significant
(F = 0.133, p = 0.875).
Index End
163
Friedman test
The Friedman test is similar to the parametric repeated measures ANOVA.
You perform a Friedman test when you have one within-subjects
independent variable with two or more levels and a dependent variable that
is not interval and normally distributed (but at least ordinal). We will use
this test to determine if there is a difference in the reading, writing and
math scores. The null hypothesis in this test is that the distribution of the
ranks of each type of score (i.e., reading, writing and math) are the same.
To conduct a Friedman test, the data need to be in a long format (see the
next topic).
Menu selection:- Analyze > Nonparametric Tests
> Legacy Dialogs > K Related Samples
Syntax:-
npar tests
/friedman = read write math.
164
Friedman test
165
Friedman test
166
Friedman test
Ranks
Mean
Rank
reading
score
writing score
math score
1.96
2.04
2.01
Friedman's chi-square has a value of 0.645 and a
p-value of 0.724 and is not statistically
significant. Hence, there is no evidence that the
distributions of the three types of scores are
different.
Test Statisticsa
N
200
Chi.645
Square
df
2
Asymp.
.724
Sig.
a. Friedman Test
Index End
167
Reshaping data
This example illustrates a wide data file and reshapes it into long form.
Consider the data containing children and their heights at one year of age
(ht1) and at two years of age (ht2).
FAMID
BIRTH
HT1
HT2
1.00
1.00
1.00
2.00
2.00
2.00
3.00
3.00
3.00
1.00
2.00
3.00
1.00
2.00
3.00
1.00
2.00
3.00
2.80
2.90
2.20
2.00
1.80
1.90
2.20
2.30
2.10
3.40
3.80
2.90
3.20
2.80
2.40
3.30
3.40
2.90
Number of cases read:
9
Number of cases listed:
9
This is called a wide format since the heights are wide. We may want the
data to be long, where each height is in a separate observation.
168
Reshaping data
FAMID
BIRTH
1.00
1.00
1.00
1.00
1.00
1.00
2.00
2.00
2.00
2.00
2.00
2.00
3.00
3.00
3.00
3.00
3.00
3.00
1.00
1.00
2.00
2.00
3.00
3.00
1.00
1.00
2.00
2.00
3.00
3.00
1.00
1.00
2.00
2.00
3.00
3.00
Number of cases read:
AGE
HT
1.00
2.00
1.00
2.00
1.00
2.00
1.00
2.00
1.00
2.00
1.00
2.00
1.00
2.00
1.00
2.00
1.00
2.00
18
2.80
3.40
2.90
3.80
2.20
2.90
2.00
3.20
1.80
2.80
1.90
2.40
2.20
3.30
2.30
3.40
2.10
2.90
We may want the data to be long, where
each height is in a separate observation.
Data may be restructured using the point
and click function in SPSS, or preprocessing with Excel.
Number of cases listed:
18
Index End
169
Ordered logistic regression
Ordered logistic regression is used when the dependent variable is
ordered, but not continuous. For example, using the A data file we will
create an ordered variable called write3, to use in our logistic
regression. This variable will have the values 1, 2 and 3, indicating a low,
medium or high writing score. We do not generally recommend
categorizing a continuous variable in this way;
we are simply creating a variable to use for this example.
Menu selection:- Transform > Recode into Different Variables
Syntax:-
if write ge 30 and write le 48 write3 = 1.
if write ge 49 and write le 57 write3 = 2.
if write ge 58 and write le 70 write3 = 3.
execute.
In Excel use =IF(H2>=58,3,IF(H2>=49,2,1)) or
=IF(H2<=48,1,IF(H2<=57,2,3))170
Ordered logistic regression
First compute the new variable.
171
Ordered logistic regression
Choose a sensible name.
Then select Old and New Values
172
Ordered logistic regression
“Add” to create rules and finally “Change”
173
Ordered logistic regression
finally “continue”
174
Ordered logistic regression
use “change” to execute
175
Ordered logistic regression
We will use gender (female), reading score (read) and social studies score
(socst) as predictor variables in this model, against our new variable
(write3). We will use a logit link and on the print subcommand we have
requested the parameter estimates, the (model) summary statistics and
the test of the parallel lines assumption.
Menu selection:- Analyze > Regression > Ordinal
Syntax:-
plum write3 with female read socst
/link = logit
/print = parameter summary tparallel.
176
Ordered logistic regression
177
Ordered logistic regression
178
Ordered logistic regression
179
Ordered logistic regression
Case Processing Summary
Marginal
N
Percentage
write3 1.00
61
30.5%
2.00
61
30.5%
3.00
78
39.0%
Valid
200
100.0%
Missing
0
Total
200
Model Fitting Information
-2 Log
Model
Likelihood
Chi-Square
Intercept Only
376.226
Final
252.151
124.075
Link function: Logit.
cThe results indicate that the overall model is statistically
df
Sig.
3
.000
Pseudo R-Square
Cox and Snell
.462
Nagelkerke
.521
McFadden
.284
Link function: Logit.
Threshold
Location
[write3 = 1.00]
[write3 = 2.00]
female
read
socst
Parameter Estimates
Estimate
Std. Error
9.704
1.203
11.800
1.312
1.285
.322
.118
.022
.080
.019
Wald
65.109
80.868
15.887
29.867
17.781
df
Parameter Estimates
95% Confidence Interval
Lower Bound
Upper Bound
Threshold
[write3 = 1.00]
7.347
12.061
[write3 = 2.00]
9.228
14.372
Location
female
.653
1.918
read
.076
.160
socst
.043
.117
Link function: Logit.
Test of Parallel Linesa
-2 Log
Model
Likelihood
Chi-Square
df
Sig.
Null Hypothesis
252.151
General
250.104
2.047
3
.563
The null hypothesis states that the location parameters (slope coefficients)
are the same across response categories.
a. Link function: Logit.
1
1
1
1
1
Sig.
.000
.000
.000
.000
.000
significant (p < .0005), as are each of the predictor
variables (p < .0005). There are two thresholds for this
model because there are three levels of the outcome
variable. We also see that the test of the proportional odds
cassumption is non-significant (p = 0.563).
One of the assumptions underlying ordinal logistic (and
ordinal probit) regression is that the relationship between
each pair of outcome groups is the same. In other words,
ordinal logistic regression assumes that the coefficients
that describe the relationship between, say, the lowest
versus all higher categories of the response variable are
the same as those that describe the relationship between
the next lowest category and all higher categories, etc.
This is called the proportional odds assumption or the
parallel regression assumption. Because the relationship
between all pairs of groups is the same, there is only one
set of coefficients (only one model). If this was not the
case, we would need different models (such as a generalized
ordered logit model) to describe the relationship between
each pair of outcome groups.
Index End
180
Factorial logistic regression
A factorial logistic regression is used when you have two or more categorical
independent variables but a dichotomous dependent variable. For example,
using the A data file we will use female as our dependent variable, because it
is the only dichotomous variable in our data set; certainly not because it is
common practice to use gender as an outcome variable. We will use type of
program (prog) and school type (schtyp) as our predictor variables. Because
prog is a categorical variable (it has three levels), we need to create dummy
codes for it. SPSS will do this for you by making dummy codes for all
variables listed after the keyword with. SPSS will also create the interaction
term; simply list the two variables that will make up the interaction
separated by the keyword by.
Menu selection:- Analyze > Regression > Binary Logistic
Simplest to realise via the syntax window.
Syntax:-
logistic regression female with prog schtyp prog by schtyp
/contrast(prog) = indicator(1).
181
Factorial logistic regression
182
Factorial logistic regression
Note that the identification of prog as the categorical variable is made
below.
183
Factorial logistic regression
Use Ctrl with left mouse key to select two variables then >a*b> for the
product term.
184
Factorial logistic regression
Define categorical variables
185
Factorial logistic regression
Indicator(1) identifies value 1 as the (first) reference category
186
Factorial logistic regression
Variables in the Equation
Case Processing Summary
Unweighted Casesa
B
N
Selected Cases
Included in Analysis
Percent
200
Missing Cases
Total
Constant
0
.0
100.0
0
.0
200
100.0
Variables
Dependent Variable Encoding
Internal Value
0
female
1
df
1.616
Sig.
1
Score
Step 0
of cases.
male
Wald
.142
Exp(B)
.204
1.198
Variables not in the Equation
a. If weight is in effect, see classification table for the total number
Original Value
S.E.
.180
100.0
200
Unselected Cases
Total
Step 0
df
Sig.
Prog
.053
2
.974
prog(1)
.049
1
.826
prog(2)
.007
1
.935
Schtyp
.047
1
.828
prog * schtyp
.031
2
.985
prog(1) by schtyp
.004
1
.950
prog(2) by schtyp
.011
1
.917
2.923
5
.712
Overall Statistics
Block 1: Method = Enter
Categorical Variables Codings
Parameter coding
Frequency
type of program
general
(1)
Omnibus Tests of Model Coefficients
(2)
45
.000
.000
academic
105
1.000
vocation
50
.000
Chi-square
Step 1
df
Sig.
Step
3.147
5
.677
.000
Block
3.147
5
.677
1.000
Model
3.147
5
.677
Loads of output!!
Block 0: Beginning Block
Model Summary
Classification Tablea,b
Predicted
female
Observed
Step 0
female
male
Step
Percentage
female
1
Correct
Cox & Snell R
Nagelkerke R
likelihood
Square
Square
272.490a
.016
.021
a. Estimation terminated at iteration number 4 because
Male
0
91
.0
Female
0
109
100.0
Overall Percentage
-2 Log
parameter estimates changed by less than .001.
54.5
Classification Tablea
a. Constant is included in the model.
Predicted
b. The cut value is .500
female
Observed
Step 1
female
male
Percentage
female
Correct
Male
32
59
35.2
Female
31
78
71.6
Overall Percentage
a. The cut value is .500
55.0
187
Factorial logistic regression
Omnibus Tests of Model Coefficients
Chi-square
Step 1
df
Sig.
Step
3.147
5
.677
Block
3.147
5
.677
Model
3.147
5
.677
The results indicate that the overall model is not statistically
significant (Likelihood ratio Chi2 = 3.147, p = 0.677). Furthermore, none
of the coefficients are statistically significant either. This shows that
the overall effect of prog is not significant.
Index End
188
Correlation
A correlation (Pearson correlation) is useful when you want to see the
relationship between two (or more) normally distributed interval variables.
For example, using the A data file we can run a correlation between two
continuous variables, read and write.
Menu selection:- Analyze > Correlate > Bivariate
Syntax:-
correlations
/variables = read write.
Understanding and Interpreting Correlations - an Interactive Visualization
189
Correlation
190
Correlation
Select Pearson
191
Correlation
Correlations
reading score
reading score
Pearson Correlation
writing score
1
Sig. (2-tailed)
writing score
.597
.000
N
200
200
Pearson Correlation
.597
1
Sig. (2-tailed)
.000
N
200
200
In the first example above, we see that the correlation between read
and write is 0.597. By squaring the correlation and then multiplying by
100, you can determine what percentage of the variability is shared,
0.597 when squared is .356409, multiplied by 100 would be 36%. Hence
read shares about 36% of its variability with write.
No need for diagonal entries, nor to duplicate the results!
192
Correlation
As a rule of thumb use the following guide for the absolute value of correlation (r):
.00-.19 “very weak”
.20-.39 “weak”
.40-.59 “moderate”
.60-.79 “strong”
.80-1.0 “very strong”
Which is based on the coefficient of
determination (r2). Which indicates the
proportion of variance in each of two
correlated variables which is shared by
both.
An index of the degree of lack of
relationship is also available. It is the
square root of the proportion of
unexplained variance and is called the
coefficient of alienation (1-r2)½. This in
turn leads to an estimate of error
reduction 1-(1-r2)½.
A Graphic and Tabular Aid To Interpreting Correlation Coefficients J.F. Voorhees Monthly Weather Review 54 423
1931926.
Correlation
In the second example, we will run a correlation between a dichotomous
variable, female, and a continuous variable, write. Although it is assumed
that the variables are interval and normally distributed, we can include
dummy variables when performing correlations.
Menu selection:- Analyze > Correlate > Bivariate
Syntax:-
correlations
/variables = female write.
194
Correlation
Correlations
female
female
Pearson Correlation
writing score
1
Sig. (2-tailed)
writing score
.256
.000
N
200
200
Pearson Correlation
.256
1
Sig. (2-tailed)
.000
N
200
200
In the output for the second example, we can see the correlation
between write and female is 0.256. Squaring this number yields
.065536, meaning that female shares approximately 6.5% of its
variability with write.
195
Correlation
An APA Results Section For
A Table Of Correlations
Correlation coefficients were computed among the five self-concept
scales. Using the Bonferroni approach to control for Type I error
across the 10 correlations, a p value of less than .005 (.05/10 = .005)
was required for significance. The results of the correlational analyses
presented in the table show that 7 out of the 10 correlations were
statistically significant and were greater than or equal to .35 (the
critical value at p = .005 and N-2 degrees of freedom).
My note!
Five variables, 5×4 = 20, but all pairs are duplicated, so 10 correlations
Index End
196
Simple linear regression
Simple linear regression allows us to look at the linear relationship
between one normally distributed interval predictor and one normally
distributed interval outcome variable. For example, using the A data file,
say we wish to look at the relationship between writing scores (write) and
reading scores (read); in other words, predicting write from read.
Menu selection:- Analyze > Regression > Linear Regression
Syntax:-
regression
/missing listwise
/statistics coeff outs ci(95) r anova
/criteria=pin(.05) pout(.10)
/noorigin
/dependent write
/method=enter read.
To investigate necessary sample size employ or PS (PowerSampleSize).
Regression analysis Crichton, N. Journal Of Clinical Nursing 10(4) 462-462 2001
Information point: coefficient of determination, R2 Crichton, N. Journal Of Clinical Nursing 8(4)
379-279 1999
197
Simple linear regression
198
Simple linear regression
199
Simple linear regression
200
Simple linear regression
Variables Entered/Removedb
Variables
Variables
Entered
Removed
Model
1
reading score
Method
We see that the relationship
between write and read is positive
(.552) and based on the t-value
(10.47) and p-value (<0.0005), we
would conclude this relationship is
statistically significant. Hence, we
would say there is a statistically
significant positive linear
relationship between reading and
writing.
. Enter
a. All requested variables entered.
b. Dependent Variable: writing score
Model Summary
Model
R
1
.597
Adjusted R
Std. Error of the
Square
Estimate
R Square
a
.356
.353
7.62487
a. Predictors: (Constant), reading score
ANOVAb
Model
1
Sum of Squares
Regression
df
Mean Square
6367.421
1
6367.421
Residual
11511.454
198
58.139
Total
17878.875
199
F
Sig.
109.521
.000a
a. Predictors: (Constant), reading score
b. Dependent Variable: writing score
Coefficientsa
Standardized
Unstandardized Coefficients
Model
1
B
(Constant)
Std. Error
23.959
2.806
.552
.053
reading score
Coefficients
Beta
t
.597
Sig.
8.539
.000
10.465
.000
Take care with in/dependent
assumptions.
a. Dependent Variable: writing score
201
Simple linear regression - Plot
Graphs > Legacy Dialogs > Scatter/Dot
Simple
scatter
Syntax
GRAPH
/SCATTERPLOT(BIVAR)=read WITH write
/MISSING=LISTWISE.
Note that the fitted line must be added interactively.
202
Simple linear regression - Plot
203
Simple linear regression - Plot
204
Simple linear regression - Plot
To fit a line
1. Open the output file
2. Double click on the graph (the chart editor will open)
3. Click on the reference line icon
4. Click apply and close
205
Simple linear regression - Plot
206
Simple linear regression
An APA Results Section
Coefficients
Model
a
95.0% Confidence Interval for B
Lower Bound
(Constant)
Index End
Upper Bound
18.426
29.492
.448
.656
1
reading score
a. Dependent Variable: writing score
A linear regression analysis was conducted to evaluate the prediction of
writing score from the reading score. The scatterplot for the two variables, is
shown, indicates that the two variables are linearly related such that as
reading score increases the writing score increases. The regression equation
for predicting the writing score is
Writing score = .552 Reading score + 23.959
The 95% confidence interval for the slope, .448 to .656 does not contain the
value of zero. Therefore overall strength is significantly related to the overall
injury index. The correlation between the reading and writing scores was .60.
Approximately 36% of the variance of the writing score was accounted for by
207
its linear relationship with the reading score.
Non-parametric correlation
A Spearman correlation is used when one or both of the variables are
not assumed to be normally distributed and interval (but are assumed to
be ordinal). The values of the variables are converted to ranks and then
correlated. In our example, we will look for a relationship between read
and write. We will not assume that both of these variables are normal
and interval.
Menu selection:- Analyze > Correlate > Bivariate
Syntax:-
nonpar corr
/variables = read write
/print = spearman.
208
Non-parametric correlation
209
Non-parametric correlation
Select Spearman
210
Non-parametric correlation
Correlations
reading score
Spearman's rho
reading score
Correlation Coefficient
1.000
.617
.
.000
N
200
200
Correlation Coefficient
.617
1.000
Sig. (2-tailed)
.000
.
N
200
200
Sig. (2-tailed)
writing score
writing score
The results suggest that the relationship between read and write
( = 0.617, p < 0.0005) is statistically significant.
211
Non-parametric correlation
Spearman’s correlation works by calculating Pearson’s correlation on
the ranked values of this data. Ranking (from low to high) is obtained
by assigning a rank of 1 to the lowest value, 2 to the next lowest and
so on. Thus the p value is only “correct” if there are no ties in the
data. In the event that ties occur an exact calculation should be
employed. SPSS does not do this. However the estimated value is
usually reliable enough.
Comparison Of Values Of Pearson’s And Spearman’s Correlation
Coefficients On The Same Sets Of Data
Jan Hauke and Tomasz Kossowski
Quaestiones Geographicae 2011 30(2) 87-93
Index End
212
Simple logistic regression
Logistic regression assumes that the outcome variable is binary (i.e.,
coded as 0 and 1). We have only one variable in the A data file that is
coded 0 and 1, and that is female. We understand that female is a silly
outcome variable (it would make more sense to use it as a predictor
variable). But we can use female as the outcome variable to illustrate
how the code for this command is structured and how to interpret the
output. The first variable listed after the logistic command is the
outcome (or dependent) variable, and all of the rest of the variables
are predictor (or independent) variables. In our example, female will be
the outcome variable, and read will be the predictor variable. As with
ordinary least squares regression, the predictor variables must be
either dichotomous or continuous; they cannot be categorical.
Menu selection:- Analyze > Regression > Binary Logistic
Syntax:-
logistic regression female with read.
213
Simple logistic regression
214
Simple logistic regression
215
Simple logistic regression
Block 1: Method = Enter
Case Processing Summary
Unweighted Casesa
Selected Cases
N
Included in Analysis
Percent
200
100.0
0
.0
Missing Cases
Total
200
Chi-square
Step 1
100.0
df
Sig.
Step
.564
1
.453
.564
1
.453
.564
1
.453
0
.0
Block
200
100.0
Model
Unselected Cases
Total
Omnibus Tests of Model Coefficients
a. If weight is in effect, see classification table for the total number
of cases.
Model Summary
Dependent Variable Encoding
Original Value
Step
Loads of output!!
Internal Value
male
0
female
1
-2 Log
Cox & Snell R
Nagelkerke R
likelihood
Square
Square
275.073a
1
.003
.004
a. Estimation terminated at iteration number 3 because
parameter estimates changed by less than .001.
Block 0: Beginning Block
Classification Tablea
Predicted
Classification Tablea,b
female
Predicted
Observed
female
Observed
Step 0
female
male
Percentage
female
Step 1
female
Correct
male
0
91
.0
female
0
109
100.0
Overall Percentage
male
4
87
4.4
female
5
104
95.4
Overall Percentage
54.0
a. The cut value is .500
54.5
Variables in the Equation
b. The cut value is .500
B
Step 1a
Variables in the Equation
B
Constant
Correct
male
a. Constant is included in the model.
Step 0
Percentage
female
S.E.
.180
Wald
.142
read
Constant
df
1.616
Sig.
1
.204
Exp(B)
S.E.
Wald
df
Sig.
Exp(B)
-.010
.014
.562
1
.453
.990
.726
.742
.958
1
.328
2.067
a. Variable(s) entered on step 1: read.
1.198
Variables not in the Equation
Score
Step 0
Variables
df
Sig.
read
.564
1
.453
Overall Statistics
.564
1
.453
216
Simple logistic regression
Block 1: Method = Enter
Omnibus Tests of Model Coefficients
Chi-square
Step 1
df
The results indicate that reading score
(read) is not a statistically significant
predictor of gender (i.e., being
female), Wald = 0.562, p = 0.453.
Likewise, the test of the overall model
is not statistically significant,
likelihood ratio Chi-squared = 0.564,
p = 0.453.
Sig.
Step
.564
1
.453
Block
.564
1
.453
Model
.564
1
.453
Model Summary
Step
-2 Log
Cox & Snell R
Nagelkerke R
likelihood
Square
Square
275.073a
1
.003
.004
a. Estimation terminated at iteration number 3 because
parameter estimates changed by less than .001.
Classification Tablea
Predicted
female
Observed
Step 1
female
male
Percentage
female
Correct
male
4
87
4.4
female
5
104
95.4
Overall Percentage
54.0
a. The cut value is .500
Variables in the Equation
B
Step 1a
read
Constant
S.E.
Wald
df
Sig.
Exp(B)
-.010
.014
.562
1
.453
.990
.726
.742
.958
1
.328
2.067
a. Variable(s) entered on step 1: read.
Index End
217
Multiple regression
Multiple regression is very similar to simple regression, except that in
multiple regression you have more than one predictor variable in the
equation. For example, using the A data file we will predict writing score
(write) from gender (female), reading (read), math, science and social
studies (socst) scores.
Menu selection:- Analyze > Regression > Linear Regression
Syntax:-
regression variable = write female read math science socst
/dependent = write
/method = enter.
To investigate necessary sample size employ.
218
Multiple regression
219
Multiple regression
Note additional independent variables within box
220
Multiple regression
Variables Entered/Removedb
Model
1
Variables
Variables
Entered
Removed
social studies
Method
. Enter
score, female,
science score,
The results indicate that the
overall model is statistically
significant (F = 58.60,
p < 0.0005). Furthermore, all of
the predictor variables are
statistically significant except
for read.
math score,
reading score
a. All requested variables entered.
b. Dependent Variable: writing score
Model Summary
Model
R
R Square
.776a
1
Adjusted R
Std. Error of the
Square
Estimate
.602
.591
6.05897
a. Predictors: (Constant), social studies score, female, science score,
math score, reading score
ANOVAb
Model
1
Sum of Squares
Regression
Residual
Total
df
Mean Square
10756.924
5
2151.385
7121.951
194
36.711
17878.875
199
F
Sig.
.000a
58.603
a. Predictors: (Constant), social studies score, female, science score, math score, reading score
b. Dependent Variable: writing score
Coefficientsa
Standardized
Unstandardized Coefficients
Model
1
B
Std. Error
(Constant)
6.139
2.808
female
5.493
.875
reading score
.125
math score
Coefficients
t
Beta
Sig.
2.186
.030
.289
6.274
.000
.065
.136
1.931
.055
.238
.067
.235
3.547
.000
science score
.242
.061
.253
3.986
.000
social studies score
.229
.053
.260
4.339
.000
a. Dependent Variable: writing score
221
Multiple regression
An APA Results Section
A multiple regression analysis was conducted to evaluate how well gender, reading and
math scores predicted writing score. The predictors were the three indices, while the
criterion variable was the writing score. The linear combination of measures was
significantly related to the score, F (5, 194) = 58.6, p <.0005. The sample multiple
correlation coefficient was .78, indicating that approximately 60% (.7762 = .602) of the
variance of the writing score in the sample can be accounted for by the linear
combination of the other measures. The table (coefficients table above) presents
indices to indicate the relative strength of the variables.
My notes!
222
Multiple regression Alternatives
There are problems with stepwise model selection procedures. These notes
are a health warning.
Various algorithms have been developed for aiding in model selection. Many
of them are “automatic”, in the sense that they have a “stopping rule”
(which it might be possible for the researcher to set or change from a
default value) based on criteria such as value of a t-statistic or an Fstatistic. Others might be better termed “semi-automatic,” in the sense
that they automatically list various options and values of measures that
might be used to help evaluate them.
Caution: Different regression software may use the same name (e.g.,
“Forward Selection” or “Backward Elimination”) to designate different
algorithms. Be sure to read the documentation to know find out just what
the algorithm does in the software you are using - in particular, whether it
has a stopping rule or is of the “semi-automatic” variety.
223
Multiple regression Alternatives
The reasons for not using a stepwise procedure are as follows.
There is a great deal of arbitrariness in the procedures. Forwards and
backwards stepwise methods will in general give different “best
models”. There are differing criteria for accepting or rejecting a
variable at any stage and also for when to stop and declare the current
model “best”.
The process gives a false impression of statistical sophistication. Often
a complex stepwise analysis is presented, when no proper thought has
been given to the real issues involved.
224
Multiple regression Alternatives
Stepwise regressions are nevertheless important for three reasons.
First, to emphasise that there is a considerable problem in choosing a
model out of so many, so considerable that a variety of automated
procedures have been devised to “help”.
Second to show that while purely statistical methods of choice can be
constructed, they are unsatisfactory.
And third, because they are fairly popular ways of avoiding constructive
thinking about model selection, you may well come across them.
You should know that they exist and roughly how they work.
225
Multiple regression Alternatives
Stepwise regressions probably do have a useful role to play, when there
are large numbers of x-variables,
when all prior information is taken
inclusion/exclusion of variables, and
carefully
into
account
in
when the results are used as a preliminary sifting of the many xvariables.
It would be rare for a stepwise regression to produce convincing
evidence for or against a scientific hypothesis.
226
Multiple regression Alternatives
“... perhaps the most serious source of error lies in letting
statistical procedures make decisions for you.”
Good P.I. and Hardin J.W., Common Errors in Statistics (and How
to Avoid Them), 4th Edition, Wiley, 2012, p. 3.
“Don't be too quick to turn on the computer. By passing the brain
to compute by reflex is a sure recipe for disaster.”
Good P.I. and Hardin J.W., Common Errors in Statistics (and How
to Avoid Them), 4th Edition, Wiley, 2012, p. 152.
227
Multiple regression Alternatives
“We do not recommend such stopping rules for routine use since
they can reject perfectly reasonable sub-models from further
consideration. Stepwise procedures are easy to explain,
inexpensive to compute, and widely used. The comparative
simplicity of the results from stepwise regression with model
selection rules appeals to many analysts. But, such algorithmic
model selection methods must be used with caution.”
Cook R.D. and Weisberg S., Applied Regression Including
Computing and Graphics, Wiley, 1999, p. 280.
228
Multiple regression Alternatives
Stopping stepwise: Why stepwise and similar selection methods
are bad, and what you should use
A common problem in regression analysis is that of variable
selection. Often, you have a large number of potential
independent variables, and wish to select among them, perhaps
to create a ‘best’ model. One common method of dealing with this
problem is some form of automated procedure, such as forward,
backward, or stepwise selection. We show that these methods
are not to be recommended, and present better alternatives
using PROC GLMSELECT and other methods.
Contains useful references, is based on SAS.
229
Multiple regression Alternatives
In a large world where parameters need to be estimated from
small or unreliable samples, the function between predictive
accuracy and the flexibility of a model (e.g., number of free
parameters) is typically inversely U shaped. Both too few and too
many parameters can hurt performance. Competing models of
strategies should be tested for their predictive ability, not their
ability to fit already known data.
Pitt M.A., Myung I.J. and Zhang S. 2002. “Toward a method for
selecting among computational models for cognition” Psychol. Rev.
109 472–491 DOI: 10.1037/0033-295X.109.3.472
230
Multiple regression Alternatives
What strategies might we adopt?
Heuristics are a subset of strategies; strategies also include
complex regression or Bayesian models. The part of the
information that is ignored is covered by Shah and
Oppenheimer’s (2008) list of five aspects (see below). The goal
of making judgments more quickly and frugally is consistent with
the goal of effort reduction, where “frugal” is often measured
by the number of cues that a heuristic searches.
231
Multiple regression Alternatives
Many definitions of heuristics exist, Shah and Oppenheimer
(2008) proposed that all heuristics rely on effort reduction by
one or more of the following:
(a) examining fewer cues,
(b) reducing the effort of retrieving cue values,
(c) simplifying the weighting of cues,
(d ) integrating less information,
(e) examining fewer alternatives.
Shah, A.K. and Oppenheimer, D.M. 2008 “Heuristics Made Easy:
An Effort-Reduction Framework” Psychological Bulletin 134(2)
207-222 DOI: 10.1037/0033-2909.134.2.207
232
Multiple regression Alternatives
Two alternative techniques, dominance analysis (Budescu 1993) and
relative weight analysis (Johnson 2000), have been developed that
permit more accurate partitioning of variance among correlated
predictors. Simulation research clearly shows that these measures of
importance perform quite well across a variety of conditions and are
recommended for this purpose (LeBreton et al. 2004). Despite calls
advocating for the wider use of these indices (Tonidandel and
LeBreton 2011), researchers seem reluctant to do so.
Budescu, D. V. 1993 “Dominance analysis: A new approach to the problem of relative importance of predictors in
multiple regression” Psychological Bulletin, 114, 542–551 DOI: 10.1037/0033-2909.114.3.542.
Johnson, J. W. 2000 “A heuristic method for estimating the relative weight of predictor variables in multiple
regression” Multivariate Behavioral Research, 35, 1–19 DOI: 10.1207/S15327906MBR3501_1.
LeBreton, J. M., Ployhart, R. E. and Ladd, R. T. 2004 “A Monte Carlo comparison of relative importance
methodologies” Organizational Research Methods, 7, 258–282 DOI: 10.1177/1094428104266017.
Tonidandel, S., and LeBreton, J. M. 2011 “Relative importance analyses: A useful supplement to multiple
regression analyses” Journal of Business and Psychology, 26, 1–9 DOI: 10.1007/s10869-010-9204-3.
Index End
233
Analysis of covariance
Analysis of covariance is like ANOVA, except in addition to the categorical
predictors you also have continuous predictors as well. For example, the one
way ANOVA example used write as the dependent variable and prog as the
independent variable. Let's add read as a continuous variable to this model,
as shown below.
Menu selection:- Analyze > General Linear Model > Univariate
Syntax:-
glm write with read by prog.
234
Analysis of covariance
235
Analysis of covariance
To help understand all these
applications, concentrate on the
introduction of the variables etc.
236
Analysis of covariance
Between-Subjects Factors
Value Label
type of program
N
1.00
general
45
2.00
academic
105
3.00
vocation
50
Tests of Between-Subjects Effects
Dependent Variable:writing score
Type III Sum of
Source
Squares
df
Mean Square
F
Sig.
Corrected Model
7017.681
a
3
2339.227
42.213
.000
Intercept
4867.964
1
4867.964
87.847
.000
read
3841.983
1
3841.983
69.332
.000
prog
650.260
2
325.130
5.867
.003
Error
10861.194
196
55.414
Total
574919.000
200
17878.875
199
Corrected Total
The results indicate
that even after
adjusting for the
reading score (read),
the writing scores still
significantly differ by
program type (prog),
F = 5.867, p = 0.003.
a. R Squared = 0393 (Adjusted R Squared = 0383)
Index End
237
Multiple logistic regression
Multiple logistic regression is like simple logistic regression, except that
there are two or more predictors. The predictors can be interval variables or
dummy variables, but cannot be categorical variables. If you have categorical
predictors, they should be coded into one or more dummy variables. We have
only one variable in our data set that is coded 0 and 1, and that is female. We
understand that female is a silly outcome variable (it would make more sense
to use it as a predictor variable). But we can use female as the outcome
variable to illustrate how the code for this command is structured and how
to interpret the output. The first variable listed after the logistic
regression command is the outcome (or dependent) variable, and all of the
rest of the variables are predictor (or independent) variables (listed after
the keyword with). In our example, female will be the outcome variable, and
read and write will be the predictor variables.
Menu selection:- Analyze > Regression > Binary Logistic
Syntax:-
logistic regression female with read write.
238
Multiple logistic regression
239
Multiple logistic regression
240
Multiple logistic regression
Block 1: Method = Enter
Case Processing Summary
Unweighted Cases
a
Selected Cases
N
Included in Analysis
Percent
100.0
0
.0
200
100.0
0
.0
200
100.0
Missing Cases
Total
Unselected Cases
Total
Omnibus Tests of Model Coefficients
200
Chi-square
Step 1
df
Sig.
Step
27.819
2
.000
Block
27.819
2
.000
Model
27.819
2
.000
a. If weight is in effect, see classification table for the total number
Model Summary
of cases.
Step
Dependent Variable Encoding
Original Value
0
female
1
Cox & Snell R
Nagelkerke R
likelihood
Square
Square
247.818a
1
Internal Value
male
-2 Log
.130
a. Estimation terminated at iteration number 4 because
parameter estimates changed by less than .001.
Block 0: Beginning Block
Classification Tablea
Classification Table
Predicted
a,b
female
Predicted
female
Observed
Step 0
female
Loads of output!!
.174
male
Observed
Percentage
Step 1
Correct
female
male
0
91
.0
female
0
109
100.0
Overall Percentage
female
male
Percentage
Correct
female
male
54
37
59.3
female
30
79
72.5
Overall Percentage
66.5
a. The cut value is .500
54.5
a. Constant is included in the model.
Variables in the Equation
b. The cut value is .500
B
Step 1a
Variables in the Equation
B
Step 0
Constant
S.E.
.180
Wald
.142
df
1.616
Sig.
1
.204
Exp(B)
1.198
S.E.
Wald
df
Sig.
Exp(B)
read
-.071
.020
13.125
1
.000
.931
write
.106
.022
23.075
1
.000
1.112
-1.706
.923
3.414
1
.065
.182
Constant
a. Variable(s) entered on step 1: read, write.
Variables not in the Equation
Score
Step 0
Variables
read
write
Overall Statistics
df
Sig.
.564
1
.453
13.158
1
.000
26.359
2
.000
241
Multiple logistic regression
Variables in the Equation
B
Step 1a
S.E.
Wald
df
Sig.
Exp(B)
read
-.071
.020
13.125
1
.000
.931
write
.106
.022
23.075
1
.000
1.112
-1.706
.923
3.414
1
.065
.182
Constant
a. Variable(s) entered on step 1: read, write.
These results show that both read and write
are significant predictors of female.
Index End
242
Discriminant analysis
Discriminant analysis is used when you have one or more normally
distributed interval independent variable(s) and a categorical dependent
variable. It is a multivariate technique that considers the latent
dimensions in the independent variables for predicting group membership
in the categorical dependent variable. For example, using the A data file,
say we wish to use read, write and math scores to predict the type of
program a student belongs to (prog).
Menu selection:- Analyze > Classify > Discriminant
Syntax:-
Discriminant groups = prog(1, 3)
/variables = read write math.
243
Discriminant analysis
244
Discriminant analysis
Do not forget to define the range for Prog.
245
Discriminant analysis
Analysis Case Processing Summary
Unweighted Cases
Valid
Excluded
Wilks' Lambda
N
Missing or out-of-range
Percent
Test of Function(s)
200
100.0
0
.0
0
.0
0
.0
Wilks' Lambda
Chi-square
df
Sig.
1 through 2
.734
60.619
6
.000
2
.995
.888
2
.641
group codes
At least one missing
Standardized Canonical Discriminant
discriminating variable
Both missing or out-of-
Function Coefficients
Function
range group codes and at
1
least one missing
discriminating variable
Total
Total
0
.0
200
100.0
.273
-.410
writing score
.331
1.183
math score
.582
-.656
Structure Matrix
Group Statistics
Function
Valid N (listwise)
type of program
general
academic
vocation
Unweighted
1
Weighted
-.272
reading score
45
45.000
writing score
45
45.000
reading score
.778*
-.184
math score
45
45.000
writing score
.775*
.630
reading score
105
105.000
writing score
105
105.000
math score
105
105.000
reading score
50
50.000
writing score
50
50.000
Loads of output!!
Pooled within-groups correlations
between discriminating variables and
standardized canonical discriminant
functions
Variables ordered by absolute size of
correlation within function.
50
50.000
reading score
200
200.000
each variable and any discriminant
writing score
200
200.000
function
math score
200
200.000
*. Largest absolute correlation between
Functions at Group Centroids
Analysis 1
Function
Summary of Canonical Discriminant Functions
Eigenvalues
Canonical
Function
2
.913*
math score
math score
Total
2
reading score
Eigenvalue
% of Variance
Cumulative %
Correlation
1
.356a
98.7
98.7
.513
2
.005a
1.3
100.0
.067
a. First 2 canonical discriminant functions were used in the analysis.
type of program
1
general
-.312
.119
academic
.536
-.020
vocation
-.844
-.066
2
Unstandardized canonical discriminant
functions evaluated at group means
246
Discriminant analysis
Functions at Group Centroids
Function
type of program
1
general
-.312
.119
academic
.536
-.020
vocation
-.844
-.066
2
Unstandardized canonical discriminant
functions evaluated at group means
Clearly, the SPSS output for this procedure is quite lengthy, and it is
beyond the scope of this item to explain all of it. However, the main point
is that two canonical variables are identified by the analysis, the first of
which seems to be more related to program type than the second.
Index End
247
One-way MANOVA
MANOVA (multivariate analysis of variance) is like ANOVA, except that
there are two or more dependent variables. In a one-way MANOVA,
there is one categorical independent variable and two or more dependent
variables. For example, using the A data file, say we wish to examine the
differences in read, write and math broken down by program type (prog).
Menu selection:- Analyse > General Linear Model > Multivariate
Syntax:-
glm read write math by prog.
248
One-way MANOVA
249
One-way MANOVA
250
One-way MANOVA
Between-Subjects Factors
Value Label
type of program 1.00
general
2.00
academic
3.00
vocation
Effect
Intercept
N
45
105
50
Multivariate Testsc
Value
F
Hypothesis df
.978
2883.051a
3.000
.022
2883.051a
3.000
44.355
2883.051a
3.000
44.355
2883.051a
3.000
.267
10.075
6.000
.734
10.870a
6.000
.361
11.667
6.000
.356
23.277b
3.000
Error df
Pillai's Trace
195.000
Wilks' Lambda
195.000
Hotelling's Trace
195.000
Roy's Largest Root
195.000
prog
Pillai's Trace
392.000
Wilks' Lambda
390.000
Hotelling's Trace
388.000
Roy's Largest Root
196.000
a. Exact statistic
b. The statistic is an upper bound on F that yields a lower bound on the significance level.
c. Design: Intercept + prog
Source
Corrected Model
Intercept
prog
Error
Total
Corrected Total
Tests of Between-Subjects Effects
Type III Sum of
Dependent Variable
Squares
reading score
3716.861a
writing score
3175.698b
math score
4002.104c
reading score
447178.672
writing score
460403.797
math score
453421.258
reading score
3716.861
writing score
3175.698
math score
4002.104
reading score
17202.559
writing score
14703.177
math score
13463.691
reading score
566514.000
writing score
574919.000
math score
571765.000
reading score
20919.420
writing score
17878.875
math score
17465.795
df
2
2
2
1
1
1
2
2
2
197
197
197
200
200
200
199
199
199
Mean Square
1858.431
1587.849
2001.052
447178.672
460403.797
453421.258
1858.431
1587.849
2001.052
87.323
74.635
68.344
Sig.
.000
.000
.000
.000
.000
.000
.000
.000
Concentrate on
the third table
251
One-way MANOVA
Concluding output table.
The students in the different
programs differ in their joint
distribution of read, write and math.
Index End
252
Multivariate multiple
regression
Multivariate multiple regression is used when you have two or more
dependent variables that are to be predicted from two or more
independent variables. In our example, we will predict write and read from
female, math, science and social studies (socst) scores.
Menu selection:- Analyse > General Linear Model > Multivariate
Syntax:-
glm write read with female math science socst.
253
Multivariate multiple
regression
254
Multivariate multiple
regression
255
Multivariate multiple
regression
Multivariate Testsb
Effect
Intercept
Value
Pillai's Trace
Wilks' Lambda
female
math
3.019a
.970
a
3.019
a
2.000
2.000
Error df
194.000
194.000
.051
Source
Dependent Variable
Squares
.051
Corrected Model
writing score
10620.092a
4
2655.023
reading score
b
4
3054.915
writing score
202.117
1
202.117
reading score
55.107
1
55.107
writing score
1413.528
1
1413.528
reading score
12.605
1
12.605
writing score
714.867
1
714.867
reading score
1025.673
1
1025.673
writing score
857.882
1
857.882
reading score
946.955
1
946.955
writing score
1105.653
1
1105.653
reading score
1475.810
1
1475.810
writing score
7258.783
195
37.225
reading score
8699.762
195
44.614
writing score
574919.000
200
reading score
566514.000
200
writing score
17878.875
199
reading score
20919.420
199
.031
3.019
2.000
194.000
.051
.031
3.019a
2.000
194.000
.051
Pillai's Trace
.170
19.851a
2.000
194.000
.000
Wilks' Lambda
.830
19.851a
2.000
194.000
.000
Hotelling's Trace
.205
19.851a
2.000
194.000
.000
Roy's Largest Root
.205
19.851a
2.000
194.000
.000
Pillai's Trace
.160
18.467a
2.000
194.000
.000
.840
a
.190
18.467
a
18.467
a
2.000
2.000
194.000
194.000
.000
.190
18.467
2.000
194.000
.000
Pillai's Trace
.166
19.366a
2.000
194.000
.000
.834
a
Hotelling's Trace
.200
19.366
a
19.366
a
2.000
2.000
194.000
194.000
.000
.200
19.366
2.000
194.000
.000
Pillai's Trace
.221
27.466a
2.000
194.000
.000
.779
a
Hotelling's Trace
Roy's Largest Root
.283
.283
27.466
.000
2.000
194.000
.000
a
2.000
194.000
.000
27.466
b. Design: Intercept + female + math + science + socst
194.000
a
27.466
a. Exact statistic
2.000
female
math
science
socst
Error
.000
Roy's Largest Root
Wilks' Lambda
Intercept
.000
Roy's Largest Root
Wilks' Lambda
Type III Sum of
Sig.
Roy's Largest Root
Hotelling's Trace
socst
Hypothesis df
.030
Hotelling's Trace
Wilks' Lambda
science
F
Tests of Between-Subjects Effects
Total
Corrected Total
df
12219.658
Mean Square
Concentrate on
the this table
256
Multivariate multiple
regression
Tests of Between-Subjects Effects
Source
Dependent Variable
Corrected Model
writing score
71.325
.000
reading score
68.474
.000
writing score
5.430
.021
reading score
1.235
.268
writing score
37.973
.000
reading score
.283
.596
writing score
19.204
.000
reading score
22.990
.000
writing score
23.046
.000
reading score
21.225
.000
writing score
29.702
.000
reading score
33.079
.000
Intercept
female
math
science
socst
Error
F
Sig.
Concluding table.
These results show that all of the
variables in the model have a
statistically significant relationship with
the joint distribution of write and read.
writing score
reading score
Total
writing score
reading score
Corrected Total
writing score
reading score
a. R Squared = 0594 (Adjusted R Squared = 0586)
b. R Squared = 0584 (Adjusted R Squared = 0576)
Index End
257
Canonical correlation
Canonical correlation is a multivariate technique used to examine the
relationship between two groups of variables. For each set of variables, it
creates latent variables and looks at the relationships among the latent
variables. It assumes that all variables in the model are interval and
normally distributed. SPSS requires that each of the two groups of
variables be separated by the keyword with. There need not be an equal
number of variables in the two groups (before and after the with). In this
case {read, write} with {math, science}.
Canonical correlation are the correlations of two canonical (latent)
variables, one representing a set of independent variables, the other a set
of dependent variables. There may be more than one such linear
correlation relating the two sets of variables, with each correlation
representing a different dimension by which the independent set of
variables is related to the dependent set. The purpose of the method is to
explain the relation of the two sets of variables, not to model the
individual variables.
258
Canonical correlation
Canonical correlation analysis is the study of the linear relations between
two sets of variables. It is the multivariate extension of correlation
analysis.
Suppose you have given a group of students two tests of ten questions
each and wish to determine the overall correlation between these two
tests. Canonical correlation finds a weighted average of the questions
from the first test and correlates this with a weighted average of the
questions from the second test. The weights are constructed to maximize
the correlation between these two averages. This correlation is called the
first canonical correlation coefficient.
You can create another set of weighted averages unrelated to the first
and calculate their correlation. This correlation is the second canonical
correlation coefficient. This process continues until the number of
canonical correlations equals the number of variables in the smallest
group.
259
Canonical correlation
In statistics, canonical-correlation analysis is a way of making sense of crosscovariance matrices. If we have two vectors X = (X1, ..., Xn) and Y = (Y1, ..., Ym)
of random variables, and there are correlations among the variables, then
canonical-correlation analysis will find linear combinations of the Xi and Yj
which have maximum correlation with each other (Härdle and Léopold 2007).
T. R. Knapp notes “virtually all of the commonly encountered parametric tests
of significance can be treated as special cases of canonical-correlation
analysis, which is the general procedure for investigating the relationships
between two sets of variables.” The method was first introduced by Harold
Hotelling in 1936.
Härdle, Wolfgang and Simar, Léopold (2007). “Canonical Correlation Analysis”.
Applied Multivariate Statistical Analysis. pp. 321–330. Canonical Correlation
Analysis - Springer ISBN 978-3-540-72243-4.
Knapp, T. R. (1978). “Canonical correlation analysis: A general parametric
significance-testing system”. Psychological Bulletin 85(2): 410–416 DOI:
10.1037/0033-2909.85.2.410 .
Hotelling, H. (1936). “Relations Between Two Sets of Variates”. Biometrika 28
(3–4): 321–377 DOI: 10.1093/biomet/28.3-4.321 .
260
Canonical correlation
The manova command, for canonical correlation, is one of the SPSS
commands that can only be accessed via syntax; there is not a sequence of
pull-down menus or point-and-clicks that could arrive at this analysis.
Syntax:-
manova read write with math science
/discrim all alpha(1)
/print=sig(eigen dim).
261
Canonical correlation
- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
The output shows
the linear
EFFECT .. WITHIN CELLS Regression
Multivariate Tests of Significance (S = 2, M = -1/2, N = 97 )
combinations
Test Name
Value
Approx. F
Hypoth. DF
Error DF
Sig. of F
corresponding to
Pillais
.59783
41.99694
4.00
394.00
.000
Hotellings
1.48369
72.32964
4.00
390.00
.000
Wilks
.40249
56.47060
4.00
392.00
.000
the first canonical
Roys
.59728
Note.. F statistic for WILKS' Lambda is exact.
correlation. At the
- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - bottom of the
Eigenvalues and Canonical Correlations
Root No.
Eigenvalue
Pct.
Cum. Pct.
Canon Cor.
Sq. Cor
output are the two
1
1.48313
99.96283
99.96283
.77284
.59728
canonical
2
.00055
.03717
100.00000
.02348
.00055
- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - correlations.
- - - - - These
Dimension Reduction Analysis
results indicate
Roots
Wilks L.
F
Hypoth. DF
Error DF
Sig. of F
that the first
1 TO 2
.40249
56.47060
4.00
392.00
.000
2 TO 2
.99945
.10865
1.00
197.00
.742
canonical
- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - EFFECT .. WITHIN CELLS Regression (Cont.)
correlation is .7728.
Univariate F-tests with (2,197) D. F.
* * * * * * * * * * * * * * * * * A n a l y s i s
Variable
read
write
o f
V a r i a n c e -- Design
1 * * * * * * * * * * * * * *
Sq. Mul. R
Adj. R-sq.
Hypoth. MS
Error MS
F
Sig. of F
.51356
.43565
.50862
.42992
5371.66966
3894.42594
51.65523
51.21839
103.99081
76.03569
.000
.000
- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
262
Canonical correlation
- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
The F-test in this
output tests the
EFFECT .. WITHIN CELLS Regression
Multivariate Tests of Significance (S = 2, M = -1/2, N = 97 )
hypothesis that the
Test Name
Value
Approx. F
Hypoth. DF
Error DF
Sig. of F
first canonical
Pillais
.59783
41.99694
4.00
394.00
.000
Hotellings
1.48369
72.32964
4.00
390.00
.000
Wilks
.40249
56.47060
4.00
392.00
.000
correlation is not
Roys
.59728
Note.. F statistic for WILKS' Lambda is exact.
equal to zero.
- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - Clearly, F = 56.4706
Eigenvalues and Canonical Correlations
Root No.
Eigenvalue
Pct.
Cum. Pct.
Canon Cor.
Sq. Cor
is statistically
1
1.48313
99.96283
99.96283
.77284
.59728
significant.
2
.00055
.03717
100.00000
.02348
.00055
- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - However,
- - - - - the
Dimension Reduction Analysis
second canonical
Roots
Wilks L.
F
Hypoth. DF
Error DF
Sig. of F
correlation of .0235
1 TO 2
.40249
56.47060
4.00
392.00
.000
2 TO 2
.99945
.10865
1.00
197.00
.742
is not statistically
- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - EFFECT .. WITHIN CELLS Regression (Cont.)
significantly
Univariate F-tests with (2,197) D. F.
different from zero
Variable
Sq. Mul. R
Adj. R-sq.
Hypoth. MS
Error MS
F
Sig. of F
read
.51356
.50862
5371.66966
51.65523
103.99081
.000
(F = 0.1087,
write
.43565
.42992
3894.42594
51.21839
76.03569
.000
p- =- -0.742)
and is not
- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - interpreted.
Index End
263
* * * * * * * * * * * * * * * * * A n a l y s i s
o f
V a r i a n c e -- Design
1 * * * * * * * * * * * * * *
Factor analysis
Factor analysis is a form of exploratory multivariate analysis that is used to
either reduce the number of variables in a model or to detect relationships
among variables. All variables involved in the factor analysis need to be interval
and are assumed to be normally distributed. The goal of the analysis is to try
to identify factors which underlie the variables. There may be fewer factors
than variables, but there may not be more factors than variables. For our
example, let's suppose that we think that there are some common factors
underlying the various test scores. We will include subcommands for varimax
rotation and a plot of the eigenvalues. We will use a principal components
extraction and will retain two factors.
Menu selection:- Analyze > Dimension Reduction > Factor
Syntax:-
factor
/variables read write math science socst
/criteria factors(2)
/extraction pc
/rotation varimax
/plot eigen.
Factor analysis Crichton, N. Journal Of Clinical Nursing 10(4) 562-562 2001264
Factor analysis
265
Factor analysis
266
Factor analysis
267
Factor analysis
268
Factor analysis
Communalities
Initial
Extraction
reading score
1.000
.736
writing score
1.000
.704
math score
1.000
.750
science score
1.000
.849
social studies score
1.000
.900
Communality (which is the opposite
of uniqueness) is the proportion of
variance of the variable (i.e., read)
that is accounted for by all of the
factors taken together, and a very
low communality can indicate that a
variable may not belong with any of
the factors.
Extraction Method: Principal Component
Analysis.
Total Variance Explained
Extraction
Sums of
Squared
Initial Eigenvalues
Component
Total
% of Variance
Loadings
Cumulative %
Total
1
3.381
67.616
67.616
3.381
2
.557
11.148
78.764
.557
3
.407
8.136
86.900
4
.356
7.123
94.023
5
.299
5.977
100.000
Total Variance Explained
Extraction Sums of Squared
Loadings
Component
% of Variance
Rotation Sums of Squared Loadings
Cumulative %
Total
% of Variance
Cumulative %
1
67.616
67.616
2.113
42.267
42.267
2
11.148
78.764
1.825
36.497
78.764
3
4
5
Extraction Method: Principal Component Analysis.
269
Factor analysis
The scree plot may be useful in determining how many factors to retain.
270
Factor analysis
Component Matrixa
Component
1
2
reading score
.858
-.020
writing score
.824
.155
math score
.844
-.195
science score
.801
-.456
social studies score
.783
.536
Extraction Method: Principal Component
Analysis.
a. 2 components extracted.
Rotated Component Matrixa
Component
1
2
reading score
.650
.559
writing score
.508
.667
math score
.757
.421
science score
.900
.198
social studies score
.222
.922
Extraction Method: Principal Component
Analysis.
From the component matrix table, we can see
that all five of the test scores load onto the
first factor, while all five tend to load not so
heavily on the second factor. The purpose of
rotating the factors is to get the variables to
load either very high or very low on each factor.
In this example, because all of the variables
loaded onto factor 1 and not on factor 2, the
rotation did not aid in the interpretation.
Instead, it made the results even more difficult
to interpret.
Rotation Method: Varimax with Kaiser
Normalization.
a. Rotation converged in 3 iterations.
Component Transformation Matrix
Component
1
2
1
.742
.670
2
-.670
.742
Extraction Method: Principal
Component Analysis.
Rotation Method: Varimax with
Kaiser Normalization.
Index End
271
Normal probability
Many statistical methods require that the numeric
variables we are working with have an approximate
normal distribution. For example, t-tests,
F-tests, and regression analyses all require in some
sense that the numeric variables are approximately
normally distributed.
272
Normal probability
Following a thorough review, it is suggested
“a compelling rationalization of the widely noted
robustness of the fixed-effects ANOVA to nonnormality”.
“It has often been reported that violation of the
normality assumption should be of little concern.”
Glass, G.V., P.D. Peckham, and J.R. Sanders. 1972.
Consequences of failure to meet assumptions
underlying fixed effects analyses of variance and
covariance. Rev. Educ. Res. 42: 237-288. DOI:
10.3102/00346543042003237
273
Normal probability
Another review which also suggests alternate tests
“non-normality appeared to have little effect on Type I
error performance but could have more serious
implications for statistical power”.
Lix, L.M., J.C. Keselman, and H.J. Keselman. 1996.
Consequences of assumption violations revisited: A
quantitative review of alternatives to the one-way
analysis of variance F test. Rev. Educ. Res. 66: 579-619.
DOI: 10.3102/00346543066004579
274
Normal probability plot
Tools for Assessing Normality include
Histogram and Boxplot
Normal Quantile Plot (also called Normal
Probability Plot)
Goodness of Fit Tests such as
Anderson-Darling Test
Kolmogorov-Smirnov Test
Lillefor’s Test
Shapiro-Wilk Test
Problem: they don’t always agree!
275
Normal probability plot
You could produce conventional descriptive
statistics, a histogram with a superimposed normal
curve, and a normal scores plot also called a
normal probability plot.
The pulse data from data set C is employed.
276
Normal probability plot
Analyze
> Descriptive Statistics
> Explore
Under plots select histogram,
also normality plots with tests,
descriptive statistics and
boxplots are default options.
277
Normal probability plot
278
Normal probability plot
279
Normal probability plot
These tests are
considered in the
next section.
280
Normal probability plot
281
Normal probability plot
If the data is “normal” the non-linear vertical axis in a
probability plot should result in an approximately linear
scatter plot representing the raw data.
282
Normal probability plot
Detrended normal
P-P plots depict
the actual
deviations of data
points from the
straight horizontal
line at zero. No
specific pattern in
a detrended plot
indicates normality
of the variable.
283
Normal probability plot
284
Normal probability plot
Graphs
> Legacy Dialogs
> Histogram
Tick – display normal
curve
285
Normal probability plot
286
Normal probability plot
287
Normal probability plot
Graphs
> Legacy Dialogs
> Line
Select Simple and
Groups of Cases the
use Define to choose
the variable and select
“cum %”.
288
Normal probability plot
289
Normal probability plot
290
Normal probability plot
If you wish to superimpose a normal curve, it is probably
simpler in Excel!
291
This approach underlies the Kolmogorov-Smirnov test.
Normal probability plot
You are seeking to assess the normality of the
data. The pulse data from data set C is employed.
The P-P plot is a normal probability plot with the
data on the horizontal axis and the expected zscores if our data was normal on the vertical axis.
When our data is approximately normal the
spacing of the two will agree resulting in a plot
with observations lying on the reference line in
the normal probability plot.
The data would not appear to be “normal”.
292
Normal probability plot
Histogram of pulse
Empirical CDF of pulse
Normal
Normal
Mean
StDev
N
20
99.7
14.86
90
Mean
StDev
N
100
99.7
14.86
90
80
Percent
10
0
60
40
20
5
0
75
90
105
pulse
120
135
150
60
70
80
90
Boxplot of pulse
100
110
pulse
120
130
140
150
Probability Plot of pulse
Normal - 95% CI
99.9
Mean
StDev
N
AD
P-Value
99
95
90
Percent
Frequency
15
99.7
14.86
90
4.635
<0.005
80
70
60
50
40
30
20
10
5
1
80
90
100
110
120
130
140
150
0.1
50
pulse
Index End
75
100
pulse
125
150
293
Skewness
Skewness is a measure of the asymmetry and kurtosis is a measure of
'peakedness' of a distribution. Skewness and Kurtosis may be used to assess
normality.
Statistical notes for clinical researchers: assessing normal distribution (2) using
skewness and kurtosis
Hae-Young Kim
Restor. Dent. Endod. 2013 38(1) 52–54 DOI: 10.5395/rde.2013.38.1.52
Descriptive and inferential measures of non-normality should be a routine part
of research reporting, along with graphic displays of the frequency distribution
of important variables.
Tests for Normality and Measures of Skewness and Kurtosis: Their Place in
Research Reporting
Kenneth D. Hopkins and Douglas L. Weeks
Educational and Psychological Measurement 1990 50(4) 717-729 DOI:
10.1177/0013164490504001
Skewness and kurtosis as criteria of normality in observed frequency distributions
Thomas A. Jones
Journal of Sedimentary Research 1969 39 1622-1627 pdf
294
Skewness
The skewness is the third centralised normalised moment.
If skewness is positive, the data are positively skewed or skewed right, meaning
that the right tail of the distribution is longer than the left. If skewness is
negative, the data are negatively skewed or skewed left, meaning that the left tail
is longer.
If skewness = 0, the data are perfectly symmetrical. But a skewness of exactly zero
is quite unlikely for real-world data, so how can you interpret the skewness number?
Bulmer (1979) suggests this rule of thumb:
If skewness is less than −1 or greater than +1, the distribution is highly skewed.
If skewness is between −1 and −½ or between +½ and +1, the distribution is
moderately skewed.
If skewness is between −½ and +½, the distribution is approximately symmetric.
Bulmer, M. G. 1979. Principles of Statistics. Dover.
295
Skewness
But what do I mean by “too much for random chance to be the explanation”? To answer that, you
need to divide the sample skewness G1 by the standard error of skewness (SES) to get the test
statistic, which measures how many standard errors separate the sample skewness from zero:
test statistic: ZG1 = G1/SES where
SES 
6n(n  1)
(n  2)( n  1)( n  3)
This formula is adapted from page 85 of Cramér (1997).
The critical value of ZG1 is approximately 2. (This is a two-tailed test of skewness ≠ 0 at roughly
the 0.05 significance level.)
If ZG1 < −2, the population is very likely skewed negatively (though you don’t know by how much).
If ZG1 is between −2 and +2, you can’t reach any conclusion about the skewness of
the population: it might be symmetric, or it might be skewed in either direction.
If ZG1 > 2, the population is very likely skewed positively (though you don’t know by how much).
Cramér, Duncan 1997
Basic Statistics for Social Research, Routledge.
296
Skewness
It is available via Analyze > Descriptive Statistics > Descriptives
The syntax is
DESCRIPTIVES VARIABLES=x3 x2 x rt_x ln_x x_1 x_2 x_3
/STATISTICS=SKEWNESS.
x is the pulse data, with successive transformations following
Tukey's ladder of powers.
297
Skewness
Descriptive Statistics
N
Skewness
Statistic Statistic
x3
90
2.208
x2
90
1.885
x
90
1.550
rt_x
90
1.380
ln_x
90
1.208
x_1
90
-0.864
x_2
90
-0.526
x_3
90
-0.203
Std. Error
0.254
0.254
0.254
0.254
0.254
0.254
0.254
0.254
Ratio
8.69
7.42
6.10
5.43
4.76
-3.40
-2.07
-0.80
If the ratio is between −2 and +2, you can’t reach
any conclusion about the skewness of the population.
Index End
298
Kurtosis
The kurtosis is the fourth centralised normalised moment.
The question is similar to the question about skewness, and the answers
are similar too. You divide the sample excess kurtosis by the standard
error of kurtosis (SEK) to get the test statistic, which tells you how
many standard errors the sample excess kurtosis is from zero:
test statistic: ZG2
n 2 1
= G2 / SEK where SEK  2SES
(n  3)( n  5)
The formula is adapted from page 89 of Cramér (1979).
Cramér, Duncan 1997
Basic Statistics for Social Research, Routledge.
299
Kurtosis
The critical value of ZG2 is approximately 2. (This is a two-tailed test of
excess kurtosis ≠ 0 at approximately the 0.05 significance level.)
If ZG2 < −2, the population very likely has negative excess kurtosis
(kurtosis <3, platykurtic), though you don’t know how much.
If ZG2 is between −2 and +2, you can’t reach any conclusion about the
kurtosis: excess kurtosis might be positive, negative, or zero.
If ZG2 > +2, the population very likely has positive excess kurtosis
(kurtosis >3, leptokurtic), though you don’t know how much.
Cramér, Duncan. 1997.
Basic Statistics for Social Research. Routledge.
300
Kurtosis!
The rules for determining the type of distribution based on skewness and
kurtosis may however vary among statisticians. Evans (2007) for instance,
suggested that distribution with skewness value of greater than 1 or less than -1
could be considered as highly skewed. Those with skewness value of between 0.5
and 1 or between -1 and -0.5 is said to have moderately skewed distribution
whereas a value between 0.5 and -0.5 indicates relative symmetry. Brown (1997)
on the other hand, proposed to the practitioners to make use of the standard
error of skewness (SES) and standard error of kurtosis (SEK) in deciding
whether the tested data could be assumed to come from a normal distribution.
He suggested that the data could be assumed as normally distributed if the
skewness and kurtosis values lie within the range of ±2×SES and ±2×SEK,
respectively. Some practitioners favour one and some favour the others.
Nonetheless, skewness and kurtosis do not provide conclusive information about
normality. Hence, it is always a good practice to supplement the skewness and
kurtosis coefficients with other methods of testing normality such as the
graphical methods and formal tests of normality.
J.R. Evans, “Statistics, data analysis and decision making”, 3rd edition, Prentice
Hall, pp. 60, 2007.
J.D. Brown, “Skewness and kurtosis,” Shiken: JALT Testing & Evaluation SIG
301
Newsletter, vol. 1, pp. 18 – 20, 1997.
Kurtosis
It is available via Analyze > Descriptive Statistics > Descriptives
The syntax is
DESCRIPTIVES VARIABLES=x3 x2 x rt_x ln_x x_1 x_2 x_3
/STATISTICS=KURTOSIS.
x is the pulse data, with successive transformations
following Tukey's ladder of powers.
302
Kurtosis
Descriptive Statistics
N
Kurtosis
Statistic Statistic
x3
90
4.776
x2
90
3.356
x
90
2.162
rt_x
90
1.651
ln_x
90
1.201
x_1
90
0.480
x_2
90
-0.001
x_3
90
-0.256
Std. Error
0.503
0.503
0.503
0.503
0.503
0.503
0.503
0.503
Ratio
9.50
6.67
4.30
3.28
2.39
0.95
0.00
-0.51
If the ratio is between −2 and +2, you can’t reach
any conclusion about the kurtosis of the population.
Index End
303
Does It Really Matter?
“Students t test and more generally the ANOVA F test
are robust to non-normality” (Fayers 2011).
However
“Thus a clearer statement is that t tests and ANOVA are
‘robust against type-I errors’. This of course accords
with the enthusiasm that many researchers have in
obtaining ‘‘significant’’ p values.
The aim of the item (see next slide) is to show that typeII errors can be substantially increased if non-normality
is ignored.” (Fayers 2011).
304
Does It Really Matter?
Alphas, betas and skewy distributions: two ways of getting the
wrong answer
Peter Fayers
Adv. Health Sci. Educ. Theory Pract. 2011 16(3) 291–296 DOI:
10.1007/s10459-011-9283-6
Introduction to Robust Estimation and Hypothesis Testing (2nd ed.).
Wilcox, R. R., 2005, Burlington MA:
Elsevier Academic Press. ISBN 978-0-12-751542-7.
Robustness to Non-Normality of Common Tests for the ManySample Location Problem
Khan A. and Rayner G.D.
Journal Of Applied Mathematics And Decision Sciences, 2003, 7(4),
187:206 DOI: 10.1155/S1173912603000178
Index End
305
Tukey's ladder of powers
3
2
1
½
0
-1
-2
-3
y3
y2
y1
y
ln(y)
y-1
y-2
y-3
Cartoon
Tukey has designed a family of power transformations
(close cousin to the Box-Cox transformations, but with a
visual aspect useful to find the appropriate transformation
to promote symmetry and linearity relationships.
These transformations preserve order, preserve
proximities and are smooth functions (not producing jumps
or peaks). y1 is the untransformed (raw) variable, y0 is
replaced by the logarithm that provides the appropriate
transformation between the square root and the reciprocal.
You can also use lower and higher powers as listed, as well
intermediate ones, i.e. y2.5 will be stronger than y² but less
than y³.
Tukey, J. W. (1977) Exploratory Data Analysis. AddisonWesley, Reading, MA.
306
Tukey's ladder of powers
A transformation is simply a means of representing the data in a different
coordinate system. In addition to restoring normality, the transformation
often reduces heteroscedasticity. (Non-constancy of the variance of a
measure over the levels of the factor under study.) This is important, because
constant variance is often an assumption of parametric tests. Subsequent
statistical analyses are performed on the transformed data; the results are
interpreted with respect to the original scale of measurement.
Achieving an appropriate transformation is a trial-and-error process. A
particular transformation is applied and the new data distribution tested for
normality; if the data are still non-normal, the process is repeated.
Nevertheless, there are certain generalities that can be used to direct your
efforts, as certain types of data typically respond to particular
transformations. For example Square-root transforms are often appropriate
for count data, which tend to follow Poisson distributions. Arcsine (sin-1)
transforms are used for data that are percentages or proportions, and tend
to fit binomial distributions. Log and square-root transforms are part of a
larger class of transforms known as the ladder of powers.
307
Tukey's ladder of powers
Transform > Compute Variable
See normal probability plot section for graphical options.
308
Tukey's ladder of powers
SORT CASES BY pulse(D).
COMPUTE ID=$casenum.
EXECUTE.
Compute work = $sysmis.
if id=1 work=pulse.
Execute.
RMV /pmax=SMEAN(work).
COMPUTE pulse1=1 + pulse/pmax.
EXECUTE.
COMPUTE y3=pulse1 ** 3.
EXECUTE.
COMPUTE y2=pulse1 ** 2.
EXECUTE.
COMPUTE y=pulse1 .
EXECUTE.
COMPUTE rt_y=SQRT(pulse1).
EXECUTE.
COMPUTE ln_y=LN(pulse1).
EXECUTE.
COMPUTE y_1=pulse1 ** -1.
EXECUTE.
COMPUTE y_2=pulse1 ** -2.
EXECUTE.
COMPUTE y_3=pulse1 ** -3.
EXECUTE.
EXAMINE VARIABLES=y2 y rt_y y_1 y_2 y_3
/COMPARE VARIABLE
/PLOT=BOXPLOT
/STATISTICS=NONE
/NOTOTAL
/MISSING=LISTWISE.
The pulse data from data set
C is employed.
It is scaled by this first
compute statement to aid
interpretation of the plots.
This step is non-essential,
only aiding the graphical
presentation.
The “x” variables have not
been scaled, being simply
powers of “pulse”.
309
Tukey's ladder of powers
Normal
x3
x2
20
20
15
10
10
0
0
0
00 00 00 0 0 0 0 0 0 00
00 00 00 0 0 0 0 0 0 00
5 0 1 00 1 50 2 0 0 25 0 30 0 3 50
Frequency
x1
30
0
0 0 00 0 0 00 0 00 0 00 00 0 00 0
30
6
9 12
15 18
21
x0
75
x 1/2
16
16
10
8
8
0
3
4.
4
4.
4.
5
4.
6
4.
7
8
4.
9
4.
5.
0
0
12
5
13
0
15
0
4
8.
x-2
5
10
x-1
20
0
90
0
9.
9.
6
.2
. 8 1 .4 2 .0
10 10
1
1
0.
7
8
9
0
1
2
3
00 .0 0 .0 0 .0 1 .01 .01 .0 1
0
0
0
0
0
0
x-3
16
10
8
5
0
0
4
6
8
0
2
4
6
00
00
00
01
01
01
01
00 .0 0 .00 .0 0 .00 .0 0 .00
0.
0
0
0
0
0
0
3
6
9
2
5
8
00
00
00
01
01
01
0 0 0 00 00 0 0 00 00 0 0 00
0
0
0
0
0
0
0
0.
0.
0.
0.
0.
0.
Which appears most “normal”?
x-2 x-3
310
Tukey's ladder of powers
Normal - 95% CI
x3
99.9
99
90
90
50
50
50
10
10
10
1
0.1
1
0.1
1
0.1
2000000
4000000
x0
99.9
99
0
10000
20000
x 1/2
99.9
99
50
99.9
99
90
90
90
50
50
50
10
10
10
1
0.1
1
0.1
4.0
99.9
99
4.5
5.0
x-2
99.9
99
90
90
50
50
10
10
1
0.1
1
0.1
0.0000
0.0001
0.0002
8
10
x1
99.9
99
90
0
Percent
x2
99.9
99
12
1
0.1
0.005
100
150
x-1
0.010
0.015
x-3
0.000000 0.000001 0.000002
Which appears most “normal”?
x-2 x-3
311
Tukey's ladder of powers
Mean
StDev
N
AD
p-value
x3
1061245
567251
90
8.615
<0.005
x2
10158
3310
90
6.523
<0.005
x1
99.7
14.86
90
4.635
<0.005
x0
4.592
0.137
90
3.048
<0.005
x
9.96
0.711
90
3.799
<0.005
x-1
0.01022
0.001296
90
1.824
<0.005
x-2
0.000106
2.52E-05
90
0.988
0.013
x-3
1.12E-06
3.75E-07
90
0.529
0.172
In general if the normal distribution fits the data, then the
plotted points will roughly form a straight line. In addition the
plotted points will fall close to the fitted line. Also the AndersonDarling (AD) statistic will be small, and the associated p-value will
be larger than the chosen α-level (usually 0.05). So the test
rejects the hypothesis of normality when the p-value is less than
or equal to α.
312
Tukey's ladder of powers
To test for normality in SPSS
you can perform a KolmogorovSmirnov Test,
Analyze
> Nonparametric tests
> Legacy Dialogs
> 1-Sample KolmogorovSmirnov Test
313
Tukey's ladder of powers
314
Tukey's ladder of powers
315
Tukey's ladder of powers
One-Sample Kolmogorov-Smirnov Test
N
Normal Parametersa,b
Most Extreme
Differences
Mean
Std. Deviation
Absolute
Positive
Negative
Kolmogorov-Smirnov Z
Asymp. Sig. (2-tailed)
a. Test distribution is Normal.
x3
x2
x
90
90
90
1061244.5667 10158.4111 99.7000
567251.11996 3309.53301 14.85847
.255
.221
.192
.255
.221
.192
-.173
-.139
-.108
2.422
2.099
1.821
.000
.000
.003
rt_x
90
9.9599
.71097
.178
.178
-.094
1.684
.007
ln_x
90
4.5924
.13698
.163
.163
-.080
1.544
.017
x-1
90
.0102
.00130
.133
.063
-.133
1.263
.082
x-2
90
.0001
.00003
.105
.060
-.105
.993
.278
x-3
90
.0000
.00000
.079
.054
-.079
.745
.635
b. Calculated from data.
Extended to the full ladder of powers. The Asymp. Sig. (2 tailed) value is
also known as the p-value. This tells you the probability of getting the
results if the null hypothesis were actually true (i.e. it is the probability
you would be in error if you rejected the null hypothesis).
316
Tukey's ladder of powers
Despite the scaling
the log. transform
spoils the final plot.
317
Tukey's ladder of powers
You are seeking
the most normal
data visually.
Probably one of
y_1, y_2 or y_3
transforms.
318
Tukey's ladder of powers
Many statistical methods require that the numeric
variables you are working with have an approximately
normal distribution. Reality is that this is often not the
case. One of the most common departures from
normality is skewness, in particular, right skewness.
319
Tukey's ladder of powers
When the data is plotted vs.
the expected z-scores the
normal
probability
plot
shows right skewness by a
downward bending curve.
When the data is plotted vs.
the expected z-scores the
normal
probability
plot
shows left skewness by an
upward bending curve.
320
Tukey’s Ladder of Powers
Tukey (1977) describes an orderly way of reexpressing variables using a power transformation.
If a transformation for x of the type xλ, results
in an effectively linear probability plot, then we
should consider changing our measurement scale
for the rest of the statistical analysis. There is no
constraint on values of λ that we may consider.
Obviously choosing λ=1 leaves the data unchanged.
Negative values of λ are also reasonable. Tukey
(1977) suggests that it is convenient to simply
define the transformation when λ=0 to be the
logarithmic function rather than the constant 1.
321
Tukey’s Ladder of Powers
In general if the normal distribution fits the data,
then the plotted points will roughly form a
straight line. In addition the plotted points will
fall close to the fitted line. Also the AndersonDarling statistic will be small, and the associated
p-value will be larger than the chosen α-level
(usually 0.05). So the test rejects the hypothesis
of normality when the p-value is less than or equal
to α.
322
Tukey’s Ladder of Powers
To test for normality is SPSS you can perform a
Kolmogorov-Smirnov Test
Analyze > Nonparametric tests
> 1-Sample Kolmogorov-Smirnov Test
The Asymp. Sig. (2 tailed) value is also known as the
p-value. This tells you the probability of getting the
results if the null hypothesis were actually true (i.e.
it is the probability you would be in error if you
rejected the null hypothesis).
323
Tukey’s Ladder of Powers
The hypothesis are
H0
H1
the distribution of x is normal
the distribution of x is not normal
If the p-value is less than .05 (in the K-S test), you
reject the normality assumption, and if the p-value is
greater than .05, there is insufficient evidence to
suggest the distribution is not normal (meaning that you
can proceed with the assumption of normality.)
In summary if the test is significant (lower than or equal
to 0.05) implies the data is not normally distributed.
324
Tukey’s Ladder of Powers
To read more about Normality tests.
Comparisons Of Tests For Normality With A Cautionary Note
Dyer, A.R.
Biometrika 61(1) 185-189 1974 DOI: 10.1093/biomet/61.1.185
A Comparison Of Various Tests Of Normality
Yazici, Berna and Yolacan, Senay
Journal Of Statistical Computation And Simulation 77(2) 175-183 2007
DOI: 10.1080/10629360600678310
Comparisons of various types of normality tests
B. W. Yap and C. H. Sim
Journal of Statistical Computation and Simulation 81(12) 2141-2155
2011 DOI: 10.1080/00949655.2010.520163
Index End
325
Median Split
There is quite a literature to suggest that, even though
it is nice and convenient to sort people into 2 groups and
then use a t test to compare group means, you lose
considerable power. Cohen (1983) has said that breaking
subjects into two groups leads to the loss of 1/5 to 2/3
of the variance accounted for by the original variables.
The loss in power is equivalent to tossing out 1/3 to 2/3
of the sample.
The Cost Of Dichotomization or paper
Cohen, J.
Applied Psychological Measurement 7(3) 249-253 1983
326
Median Split
In Excel
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
A
B
C
D
0.801146
1
0.353356 median 0.573873 0
0.310995
0
0.745806
1
0.459178
0
0.421358
0
0.390142
0
0.594849
1
0.655845
1
0.552896
0
0.793741
1
0.768881
1
0.852641
1
0.148785
0
0.749638
1
0.415487
0
0.755597
1
0.238325
0
0.80543
1
0.305794
0
1
2
A
B
0.801146
0.353356 median
C
=MEDIAN(A1:A20)
D
=IF(A1<C$2,0,1)
=IF(A2<C$2,0,1)
In SPSS you have to find the median, say, from
Analyze > Descriptive Statistics > Frequencies
Syntax
FREQUENCIES VARIABLES=VAR00001
/FORMAT=NOTABLE
/STATISTICS=MEDIAN
/ORDER=ANALYSIS.
then transfer it manually.
Recall write3 in ordered logistic regression, as an aid 327
see the following slides.
Median Split
328
Median Split
329
Median Split
Syntax
RECODE VAR00001 (Lowest thru .573873=0) (ELSE=1) INTO split.
EXECUTE.
Index End
330
Likert Scale
These are not exhaustive notes, rather some thoughts on preparing a Likert
Scale. Some 11,000 papers employ Likert scales, many debate the issues sketched
below.
Statements are often rated on a five point Likert (1932) scale. Weijters et al.
(2010) report people completing surveys with 7-point scales are more susceptible
to extreme responding (i.e. picking one or other of the endpoints). They are also
more likely to make mistakes when just the end-points are labelled. These
authors recommend using 5-point scales with each item on the scale fully labelled
(e.g. strongly agree, agree, neutral, disagree, strongly disagree).
Likert, R. (1932). A technique for the measurement of attitudes. Archives of
Psychology, 22(140) 1-55.
Weijters, Bert; Cabooter, Elke; Schillewaert, Niels (2010) The effect of rating
scale format on response styles: The number of response categories and response
category labels. International Journal Of Research In Marketing 27(3) 236-247
331
DOI: 10.1016/j.ijresmar.2010.02.004 (see final slide in this section).
Likert Scale
Negative coding, for a Likert scale from 1 to n. If the response was x
and it need negative coding, simply form n+1-x with Excel (say). So
1→n and n→1. So for a 5 point scale form 6-x.
Test it for all possible values in your favourite scale.
2
3
4
B
n
x
negative
coding
C
5
2
2
3
4
4
B
C
n
5
x
2
negative
=C2+1-C3
coding
332
Likert Scale
However, a 7-point Likert scale is recommended to maximise the
sensitivity of the scale (Allen and Seaman 2007, Cummins and Gullone
2000), while Leung (2011) covers the full spectrum of choices.
Allen, I.E., and Seaman, C.A. (2007). Likert scales and data analyses.
Quality Progress, 40(7), 64-65.
Cummins, R.A., and Gullone, E. (2000). Why we should not use 5-point
Likert scales: The case for subjective quality of life measurement. In
Proceedings, second international conference on quality of life in
cities (p74-93). Singapore: National University of Singapore.
Leung, S-O. (2011). A Comparison of Psychometric Properties and
Normality in 4-, 5-, 6-, and 11-Point Likert Scales, Journal of Social
Service Research 37(4) 412-421 DOI:
10.1080/01488376.2011.580697 an odd place for a technical paper.333
Likert Scale
You can even cope with mixed scales. It is unclear why different
scales may have been used in the same experiment, but it has been
shown that data is still comparable when it has been re-scaled
(Dawes 2008).
Dawes J. (2008) Do data characteristics change according to the
number of scale points used? An experiment using 5 point, 7 point
and 10 point scales International Journal of Market Research. 51 (1)
61-77.
334
Likert Scale
What about a mid-point? It may be better if the scale contained a
neutral midpoint (Tsang 2012). This decision (an odd/even scale)
depends whether respondents are being forced to exclude the neutral
position with an even scale.
Tsang K.K (2012) The use of midpoint on Likert Scale: The implications for educational
research Hong Kong Teachers’ Centre Journal 11 121-130.
An odd number of points allow people to select a middle option. An even
number forces respondents to take sides. An even number is
appropriate when you want to know what direction the people in the
middle are leaning. However, forcing people to choose a side, without a
middle point, may frustrate some respondents (Wong et al. 1993).
Wong, C.-S., Tam, K.-C., Fung, M.-Y., and Wan, K. (1993). Differences between odd and
even number of response scale: Some empirical evidence. Chinese Journal of Psychology,
35, 75-86.
335
Likert Scale
Since they have no neutral point, even-numbered Likert scales force
the respondent to commit to a certain position (Brown, 2006) even if
the respondent may not have a definite opinion.
There are some researchers who prefer scales with 7 items or with
an even number of response items (Cohen, Manion, and Morrison,
2000).
Brown, J.D. (2000). What issues affect Likert-scale questionnaire
formats? JALT Testing and Evaluation SIG, 4, 27-30.
Cohen, L., Manion, L. and Morrison, K. (2000). Research methods in
education (5th ed.). London: Routledge Falmer.
336
Likert Scale
The change of response order in a Likert-type scale was found to alter
participant responses and scale characteristics. Where response
order, is the order in which options of a Likert-type scale are offered
(Weng 2000).
How many scale divisions or categories should be used (1 to 10; 1 to 7;
-3 to +3)?
Should there be an odd or even number of divisions? (Odd gives
neutral centre value; even forces respondents to take a non-neutral
position.)
What should the nature and descriptiveness of the scale labels be?
What should the physical form or layout of the scale be? (graphic,
simple linear, vertical, horizontal)
Should a response be forced or be left optional?
Li-Jen Weng 2000 Effects of Response Order on Likert-Type Scales, Educational and Psychological
Measurement 60(6) 908-924 DOI: 10.1177/00131640021970989
337
Likert Scale
Formulate recommendations on
the choice of a scale format.
Weijters et al. (2010) DOI: 10.1016/j.ijresmar.2010.02.004
Index End
338
Winsorize
Winsorising or Winsorization is a transformation by limiting extreme
values in the data to reduce the effect of possibly spurious outliers. It
is named after the engineer-turned-biostatistician Charles P. Winsor
(1895-1951).
The computation of many statistics can be heavily influenced by
extreme values. One approach to providing a more robust computation
of the statistic is to Winsorize the data before computing the
statistic.
Apart from confusion about the correct spelling. There is the
ambiguity about where the precise percentile sits.
339
Winsorize
To Winsorize the data, tail values are set equal to some specified
percentile of the data. For example, for a 90% Winsorization, the
bottom 5% of the values are set equal to the value corresponding to
the 5th percentile while the upper 5% of the values are set equal to
the value corresponding to the 95th percentile.
Just because a method exists
does not necessarily mean its
a great idea!!
340
Winsorize
The pulse data from data set C is
employed.
Analyze > Descriptive Statistics
> Frequencies
341
Winsorize
Select statistics
342
Winsorize
Add desired percentiles, 5 then 95
343
Winsorize
For brevity do not display frequency tables
344
Winsorize
Note the percentiles and enter them into the next slide.
345
Winsorize
Transform > Compute Variable
346
Winsorize
Choose a
sensible new
name
Select Old and New Values
347
Winsorize
Then Add
348
Winsorize
Then Add
349
Winsorize
Retain all
other values
Then Add
350
Winsorize
Finally, continue then OK
351
Winsorize
To check your results
Analyze > Descriptive Statistics
> Descriptives
352
Winsorize
OK
353
Winsorize
As desired.
354
Winsorize
Syntax:-
freq var pulse /format = notable /percentiles = 5 95.
compute winsor = pulse.
if pulse <= 83 winsor = 83.
if pulse >= 137.25 winsor = 137.25.
descriptives variables=pulse winsor
/statistics=mean stddev min max.
355
Winsorize
This paper provides a literature review for robust statistical
procedures trimming and Winsorization that were first proposed for
estimating location, but were later extended to other estimation and
testing problems. Performance of these techniques under normal and
long-tailed distributions are discussed.
Trimming and Winsorization: A review
W. J. Dixon and K. K. Yuen
Statistische Hefte
June 1974, Volume 15, Issue 2-3, pp 157-170
356
Winsorize
Outliers are a common problem in business surveys which, if left untreated, can have a
large impact on survey estimates. For business surveys in the UK Office for National
Statistics (ONS), outliers are often treated by modifying their values using a treatment
known as Winsorisation. The method involves identifying a cut-off for outliers. Any
values lying above the cut-offs are reduced towards the cut-off. The cut-offs are
derived in a way that approximately minimises the Mean Square Error of level estimates.
However, for many surveys estimates of change are more important. This paper looks at
a variety of methods for Winsorising specifically for estimates of change. The measure
of change investigated is the difference between two consecutive estimates of total.
The first step is to derive potential methods for Winsorising this type of change. Some
of these methods prove more practical than others. The methods are then evaluated,
using change estimates derived by taking the difference between two regular
Winsorised level estimates as a comparison.
Winsorisation for estimates of change
Daniel Lewis
Papers presented at the ICES-III, June 18-21, 2007, Montreal, Quebec, Canada paper
357
Winsorize
Trimmed means are means calculated after setting aside zero or more
values in each tail of a sample distribution. Here we focus on trimming
equal numbers in each tail. Such trimmed means define a family or
function with mean and median as extreme members and are attractive
as simple and easily understood summaries of the general level
(location, central tendency) of a variable. This article provides a
tutorial review of trimmed means, emphasizing the scope for trimming
to varying degrees in describing and exploring data. Detailed remarks
are included on the idea's history, plotting of results, and confidence
interval procedures.
Note uses Stata!
Speaking Stata: Trimming to taste
Cox, N.J.
Stata Journal 2013 13(3) 640-666
Index End
358
General Linear Models
Generally, the various statistical analyses are taught independently
from each other. This makes it difficult to learn new statistical
analyses, in contexts that differ. The paper gives a short technical
introduction to the general linear model (GLM), in which it is shown
that ANOVA (one-way, factorial, repeated measure and analysis of
covariance) is simply a multiple correlation/regression analysis (MCRA).
Generalizations to other cases, such as multivariate and nonlinear
analysis, are also discussed. It can easily be shown that every popular
linear analysis can be derived from understanding MCRA.
They present the identities shown on the next two slides.
General Linear Models: An Integrated Approach to Statistics
Sylvain Chartier and Andrew Faulkner
Tutorials in Quantitative Methods for Psychology 2008 4(2) 65-78
359
General Linear Models
360
General Linear Models
Index End
361
Centre Data
Sometimes to facilitate analysis it is necessary to centre a data set,
for instance to give it a mean of zero. In this case consider the
reading score in data set A.
362
Centre Data
Why center? Different authors have made different recommendations
regarding the centring of independent variables. Some have
recommended mean-centring (i.e., subtracting the mean from the value
of the original variable so that it has a mean of 0); others zstandardization (which does the same, and then divides by the
standard deviation, so that it has a mean of 0 and a standard deviation
of 1); others suggest leaving the variables in their raw form. In truth,
with the exception of cases of extreme multi-collinearity (which may
arise in multiple-regression/correlation), the decision does not make
any major difference. For instance the p value for an interaction term
any subsequent interaction plot should be identical whichever way it is
done (Dalal and Zickar 2012; Kromrey and Foster-Johnson 1998).
Dalal, D. K. and Zickar, M. J. 2012 “Some common myths about centering predictor variables in
moderated multiple regression and polynomial regression” Organizational Research
Methods, 15, 339–362 DOI: 10.1177/1094428111430540
Kromrey, J. D. and Foster-Johnson, L. 1998 “Mean centering in moderated multiple regression: Much
ado about nothing” Educational and Psychological Measurement, 58, 42–67 DOI:
10.1177/0013164498058001005
363
Centre Data
To check we have achieved our
goal we generate descriptive
statistics.
364
Centre Data
To check we have achieved our
goal we generate descriptive
statistics.
Syntax
EXAMINE VARIABLES=read
/PLOT BOXPLOT STEMLEAF
/COMPARE GROUPS
/STATISTICS
DESCRIPTIVES
/CINTERVAL 95
/MISSING LISTWISE
/NOTOTAL.
365
Centre Data
Note, the mean is 53.23.
366
Centre Data
To create a column of means.
367
Centre Data
To create a column of means.
Syntax
AGGREGATE
/OUTFILE=*
MODE=ADDVARIABLES
/BREAK=
/read_mean=MEAN(read).
368
Centre Data
Finally compute the desired variable.
369
Centre Data
Finally compute the
desired variable.
Syntax
COMPUTE read_centre=read - read_mean.
EXECUTE.
370
Centre Data
Repeat descriptive statistics on the new variable. Now zero mean.
Index End
371
Correlation - Comparison
If simply comparing two correlations, a simple web search should
reveal numerous analytic tools. Alternately see, for example,
Kanji, G.K. 1999 “100 Statistical Tests” London: SAGE.
Test 14 which includes a worked example.
1  1  r1 
1
  1 
z1  ln 
2  1  r1 
n1  3
1
1  1  r2 
  2 
z 2  ln 
2  1  r2 
n2  3
   12   22 z 
z1  z 2

372
Correlation - Comparison
Several procedures that use summary data to test hypotheses about
Pearson correlations and ordinary least squares regression
coefficients have been described in various books and articles. No
single resource describes all of the most common tests.
Furthermore, many of these tests have not yet been implemented in
popular statistical software packages such as SPSS. The article
(next slide) describes all of the most common tests and provide
SPSS programs to perform them. When they are applicable, the
code also computes 100 × (1 − α)% confidence intervals
corresponding to the tests. For testing hypotheses about
independent regression coefficients, they demonstrate one method
that uses summary data and another that uses raw data (i.e.,
Potthoff analysis). When the raw data are available, the latter
method is preferred, because use of summary data entails some loss
of precision due to rounding.
373
Correlation - Comparison
SPSS and SAS programs for comparing Pearson correlations and
OLS regression coefficients
Bruce Weaver and Karl L. Wuensch
Behavior Research Methods
September 2013, Volume 45, Issue 3, pp 880-895
DOI: 10.3758/s13428-012-0289-7
For the code access. Not the earlier version on the journal web site.
374
Correlation - Paradox
Validation of selection tests or other selection variables is most frequently
accomplished through correlation and regression. It is quite common to note
that both sexes or two ethnic groups were included in the sample. Sometimes
in the combined sex or ethnic groups the correlation of the predictor and
criterion may be moderate or large, but within each group the correlation of
predictor and criterion is low or zero. This seeming paradox is not a
psychological phenomenon, but a consequence of the mathematics of regression
and correlation. The problem would seem to require a Within and Between
Analysis, but having only two groups prohibits use of the methodology. A
general hierarchical linear models analysis is proposed and demonstrated by
the authors.
This is an example of Simpson's paradox (e.g., Agresti and Finlay, 1986, p. 320)
M.J. Ree , T.R. Carretta and J.A. Earles 1999 “In Validation Sometimes Two Sexes Are
One Too Many: A Tutorial, Human Performance”, 12(1), 79-88, DOI:
10.1207/s15327043hup1201_4
Agresti, A. and Finlay. B. (1986). Statistical methods for the social sciences (2nd ed.).
San Francisco:Dellen Publishing
375
Correlation - Paradox
Reilly et al. (1979) reported a combined sample correlation for a measure of cable-pull strength
versus training performance of .29 and male and female correlations of. 17 and. 19 respectively.
Results from a study by Jackson and Osburn (1983) correlating lean body mass with a lifting task
provided an example of an even larger increase as a result of combining groups. For men and women,
the correlations were .38 and .28, but a correlation of .74 was found when both groups were
combined.
A more radical example of combined versus single-group correlations can be found in Hogan et al.
(1979) where the two single-group correlations of grip strength and warehouse production were
negative (-.09 and -.11) and the combined group correlation was positive (.30).
Artefacts such as small sample size, differential restriction of range, and unreliable measures can
cause these counter intuitive results.
Reilly, R. R., Zedeck, S. and Tenopyr, M. L. (1979) Validity and fairness of physical ability tests for predicting performance in craft jobs,
Journal of Applied Psychology, Vol 64(3), Jun 1979, 262-274. DOI: 10.1037/0021-9010.64.3.262
Reilly, R. R., Zedeck, S. and Tenopyr, M. L. (1979) Validity and fairness of physical ability tests for predicting craft jobs – Correction, Journal
of Applied Psychology, 64, 262-274 DOI: 10.1037/h0077960
Jackson, A. S., and Osbum, H. G. (1983) Validity of isometric strength tests for predicting performance in underground coal mining tasks.
Houston, TX: Shell Oil Employment Services.
A. S. Jackson, H. G. Osburn and K. R. Laughery (1984) Validity of Isometric Strength Tests for Predicting Performance in Physically
Demanding Tasks, Proceedings of the Human Factors and Ergonomics Society Annual Meeting October 1984 vol. 28 no. 5 452-454 DOI:
10.1177/154193128402800515 or
Hogan, J. C.. Ogden, G. D. and Fleishman, E. A. (1979) Development and validation of tests for the order selector job at Certified Grocers of
California, Ltd. Washington DC: Advanced Research Resources Organization.
Index End
376
Sobel Test
The Sobel test will assess whether a mediator (see more extensive notes on
Mediation on the main web page) carries the influence of an independent
variable to a dependent variable.
The Sobel test works well only in large samples. It is recommended using this
test only if the user has no access to raw data. If you have the raw data,
bootstrapping offers a much better alternative that imposes no distributional
assumptions. Consult Preacher and Hayes (2004, 2008) for details and easy-touse macros that run the necessary regression analyses for you:
Preacher, K. J. and Hayes, A. F. (2008) “Asymptotic and resampling strategies for assessing and
comparing indirect effects in multiple mediator models” Behavior Research Methods, 40, 879-891
DOI: 10.3758/BRM.40.3.879.
Preacher, K. J., & Hayes, A. F. (2004) “SPSS and SAS procedures for estimating indirect effects in
simple Mediation models”Behavior Research Methods, Instruments, & Computers, 36, 717-731 DOI:
10.3758/BF03206553.
See How can I perform a Sobel test on a single mediation effect in SPSS?
But its not simple!
Index End
377
Structural Equation Modelling
The tutorial begins with an overview of structural equation modeling (SEM) that
includes the purpose and goals of the statistical analysis as well as terminology
unique to this technique. It focuses on confirmatory factor analysis (CFA), a
special type of SEM. After a general introduction, CFA is differentiated from
exploratory factor analysis (EFA), and the advantages of CFA techniques are
discussed. Following a brief overview, the process of modelling is discussed and
illustrated with an example using data from a HIV risk behaviour evaluation of
homeless adults (Stein and Nyamathi, 2000). Techniques for analysis of nonnormally distributed data as well as strategies for model modification are shown.
The empirical example examines the structure of drug and alcohol use problem
scales. Although these scales are not specific personality constructs, the
concepts illustrated in this article directly correspond to those found when
analysing personality scales and inventories. Computer program syntax and output
for the empirical example from a popular SEM program (EQS 6.1; Bentler, 2001)
are included.
Structural equation modeling: Reviewing the basics and moving forward
Ullman, Jodie B.
Journal Of Personality Assessment 87(1) 35-50 2006
DOI: 10.1207/s15327752jpa8701_03
378
Structural Equation Modelling
Stein, J. A. and Nyamathi, A. M. (2000). Gender differences in behavioural and
psychosocial predictors of HIV testing and return for test results in a highrisk population. AIDS Care, 12, 343–356. DOI: 10.1080/09540120050043007
Bentler, P.M. (2001). EQS 6 structural equations program manual. Encino, CA:
Multivariate Software.
Download Eqs 6 software
This page serves as a gateway to a tutorial on structural equation modeling or
SEM.
Index End
379
Quartiles
Are quartiles well defined?
Hyndman and Fan (1996) investigated nine different methods implemented in
the statistical software to calculate sample quantiles. Sample quantiles
providing nonparametric estimators of their population counterparts are based
on one or two order statistics from the sample x1,…,xn. Adopting notation used
in Hyndman and Fan (1996) let us define the p100%-th sample quantile given by
the ith method as follows

Qi ( p)  (1   ) x j:n  x j 1:n
jm
j  m 1
 p
n
n
for some constants m∈R and 0 ≤ γ ≤ 1 chosen appropriately for each method.
The value of γ is a function of j=⌊np+m⌋ and g=np+m−j. Values of these
parameters corresponding to particular methods are given in the table. For
more details on those methods we refer the reader to Hyndman and Fan
(1996).
Hyndman R.J., Fan, Y. (1996), Sample quantiles in statistical packages, The
American Statistician 50, 361-365, DOI: 10.2307/2684934
380
Quartiles
0
1
Method 1
m=0
 
Method 2
m=0
 
Method 3
m = −0.5
 
Method 4
m=0
γ=g
Method 5
m = 0.5
γ=g
Method 6
m=p
γ=g
Method 7
m=1−p
γ=g
Method 8
m = ⅓ (p + 1)
γ=g
Method 9
m=¼p+ ⅜
γ=g
if g  0
otherwise
0.5 if g  0
 1 otherwise
0
1
if g  0 and j is even
otherwise
Method 6 corresponds to Excel (quartile.exc(), also SPSS
and Minitab).
Method 7 corresponds to Excel (quartile() and
quartile.inc())
381
Quartiles
What ever method we choose, the first and the third quartiles given by
the ith method are given by

Qi (0.75)  (1   ) xk:n  xk 1:n

Qi (0.25)  (1   ) xl:n  xl 1:n
where k=⌊0.75n+m⌋ and l=⌊0.25n+m⌋. Consequently, the interquartile range
based on a sample of size n, produced by the ith method (i=1,…,9), has the
following form
IQRni  (1   )(xk:n  xl:n )   ( xk 1:n  xl 1:n )
382
Quartiles
Given the following random sorted data
0.008228533 0.012108943 0.043745942 0.054314571 0.214140779 0.251766741 0.289577348
0.290472163 0.342535936 0.384891271 0.452616365 0.463141946 0.496310054 0.603820413
0.645915266 0.739309969 0.786093766 0.813916662 0.832916098 0.951772594
Method
n
m
p
j
g
γ
l
x1
1
20
0
0.25
5
0.00
0
5
2
20
0
0.25
5
0.00
0.5
5
3
20
-0.5
0.25
4
0.50
1
4
Lower Quartile
4
5
6
20
20
20
0
0.5
0.25
0.25
0.25
0.25
5
5
5
0.00
0.50
0.25
0.00
0.50
0.25
5
5
5
7
20
0.75
0.25
5
0.75
0.75
5
8
20
0.42
0.25
5
0.42
0.42
5
9
20
0.4375
0.25
5
0.44
0.44
5
0.2141 0.2330 0.2141 0.2141 0.2330 0.2235 0.2424 0.2298 0.2306
Lower quartile x1
383
Quartiles
Given the following random sorted data
0.008228533 0.012108943 0.043745942 0.054314571 0.214140779 0.251766741 0.289577348
0.290472163 0.342535936 0.384891271 0.452616365 0.463141946 0.496310054 0.603820413
0.645915266 0.739309969 0.786093766 0.813916662 0.832916098 0.951772594
Method
n
m
p
j
g
γ
k
x3
1
20
0
0.75
15
0.00
0
15
2
20
0
0.75
15
0.00
0.5
15
3
20
-0.5
0.75
14
0.50
1
14
Upper Quartile
4
5
6
20
20
20
0
0.5
0.75
0.75
0.75
0.75
15
15
15
0.00
0.50
0.75
0.00
0.50
0.75
15
15
15
7
20
0.25
0.75
15
0.25
0.25
15
8
20
0.58
0.75
15
0.58
0.58
15
9
20
0.5625
0.75
15
0.56
0.56
15
0.6459 0.6926 0.6459 0.6459 0.6926 0.7160 0.6693 0.7004 0.6984
Upper quartile x3
Index End
384
Does It Always Matter?
Scientists think in terms of confidence intervals – they
are inclined to accept a hypothesis if the probability
that it is true exceeds 95 per cent. However within the
law “beyond reasonable doubt” appears to be a claim that
there is a high probability that the hypothesis – the
defendant’s guilt – is true.
A Story Can Be More Useful Than Maths
John Kay
Financial Times 26 February 2013
385
Does It Always Matter?
…we slavishly lean on the crutch of significance testing
because, if we didn’t, much of psychology would simply
fall apart. If he was right, then significance testing is
tantamount to psychology’s “dirty little secret.”
Significance tests as sorcery: Science is empirical significance tests are not
Charles Lambdin
Theory and Psychology 22(1) 67–90 2012
386
Does It Always Matter? Probably!
Estimation based on effect sizes, confidence intervals, and metaanalysis usually provides a more informative analysis of empirical
results than does statistical significance testing, which has long
been the conventional choice in psychology. The sixth edition of the
American Psychological Association Publication Manual now
recommends that psychologists should, wherever possible, use
estimation and base their interpretation of research results on point
and interval estimates.
The statistical recommendations of the American Psychological
Association Publication Manual: Effect sizes, confidence intervals,
and meta-analysis
Geoff Cumming, Fiona Fidler, Pav Kalinowski and Jerry Lai
Australian Journal of Psychology 2012 64 138–146
387
Does It Always Matter? Probably!
The debate is ongoing!
Cumming, G. 2014 “The new statistics: Why and how. Psychological
Science”, 25, 7-29 DOI: 10.1177/0956797613504966
Savalei V. and Dunn E. 2015 “Is the call to abandon p-values the red
herring of the replicability crisis?” Frontiers in Psychology 6:245.
DOI: 10.3389/fpsyg.2015.00245
Index End
388
SPSS Tips
Now you should go and try for yourself.
Each week a cluster is booked to follow this session.
This will enable you to come and go as you please.
Obviously other timetabled sessions for this module
take precedence.
Index
389
Does It Always Matter?
The first rule of performing a project
1
The supervisor is always right
The second rule of performing a project
2
If the supervisor is wrong, rule 1 applies
390