* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download An Introduction to Logistic Regression
Computer simulation wikipedia , lookup
K-nearest neighbors algorithm wikipedia , lookup
Vector generalized linear model wikipedia , lookup
Data assimilation wikipedia , lookup
Predictive analytics wikipedia , lookup
Plateau principle wikipedia , lookup
Least squares wikipedia , lookup
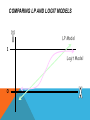
INTRODUCTION TO LOGISTIC REGRESSION ENI SUMARMININGSIH, SSI, MM PROGRAM STUDI STATISTIKA JURUSAN MATEMATIKA UNIVERSITAS BRAWIJAYA OUTLINE Introduction and Description Some Potential Problems and Solutions INTRODUCTION AND DESCRIPTION Why use logistic regression? Estimation by maximum likelihood Interpreting coefficients Hypothesis testing Evaluating the performance of the model WHY USE LOGISTIC REGRESSION? There are many important research topics for which the dependent variable is "limited." For example: voting, morbidity or mortality, and participation data is not continuous or distributed normally. Binary logistic regression is a type of regression analysis where the dependent variable is a dummy variable: coded 0 (did not vote) or 1(did vote) THE LINEAR PROBABILITY MODEL In the OLS regression: Y = + X + e ; where Y = (0, 1) The error terms are heteroskedastic e is not normally distributed because Y takes on only two values The predicted probabilities can be greater than 1 or less than 0 AN EXAMPLE You are a researcher who is interested in understanding the effect of smoking and weight upon resting pulse rate. Because you have categorized the response-pulse rate-into low and high, a binary logistic regression analysis is appropriate to investigate the effects of smoking and weight upon pulse rate. THE DATA RestingPulse Smokes Weight Low No 140 Low No 145 Low Yes 160 Low Yes 190 Low No 155 Low No 165 High No 150 Low No 190 Low No 195 ⁞ ⁞ Low No 110 High No 150 Low No 108 ⁞ OLS RESULTS Results Regression Analysis: Tekanan Darah versus Weight, Merokok The regression equation is Tekanan Darah = 0.745 - 0.00392 Weight + 0.210 Merokok Predictor Coef SE Coef T P Constant 0.7449 0.2715 2.74 0.007 Weight -0.003925 0.001876 -2.09 0.039 Merokok 0.20989 0.09626 2.18 0.032 S = 0.416246 R-Sq = 7.9% R-Sq(adj) = 5.8% PROBLEMS: Predicted Values outside the 0,1 range Descriptive Statistics: FITS1 Variable N N* FITS1 92 0 Mean StDev Minimum Q1 Median Q3 Maximum 0.2391 0.1204 -0.0989 0.1562 0.2347 0.3132 0.5309 HETEROSKEDASTICITY Scatterplot of RESI1 vs Weight 1.00 0.75 RESI1 0.50 0.25 0.00 -0.25 -0.50 100 120 140 160 Weight 180 200 220 THE LOGISTIC REGRESSION MODEL The "logit" model solves these problems: ln[p/(1-p)] = + X + e p is the probability that the event Y occurs, p(Y=1) p/(1-p) is the "odds ratio" ln[p/(1-p)] is the log odds ratio, or "logit" More: The logistic distribution constrains the estimated probabilities to lie between 0 and 1. The estimated probability is: p = 1/[1 + exp(- - X)] if you let + X =0, then p = .50 as + X gets really big, p approaches 1 as + X gets really small, p approaches 0 COMPARING LP AND LOGIT MODELS LP Model 1 Logit Model 0 MAXIMUM LIKELIHOOD ESTIMATION (MLE) MLE is a statistical method for estimating the coefficients of a model. INTERPRETING COEFFICIENTS Since: ln[p/(1-p)] = + X + e The slope coefficient () is interpreted as the rate of change in the "log odds" as X changes … not very useful. An interpretation of the logit coefficient which is usually more intuitive is the "odds ratio" Since: [p/(1-p)] = exp( + X) exp() is the effect of the independent variable on the "odds ratio" FROM MINITAB OUTPUT: Logistic Regression Table Predictor Coef SE Coef Z Constant -1.98717 1.67930 -1.18 Smokes Yes -1.19297 0.552980 -2.16 Weight 0.0250226 0.0122551 2.04 P 0.237 Odds 95% CI Ratio Lower Upper 0.031 0.30 0.10 0.90 0.041 1.03 1.00 1.05 **Although there is evidence that the estimated coefficient for Weight is not zero, the odds ratio is very close to one (1.03), indicating that a one pound increase in weight minimally effects a person's resting pulse rate **Given that subjects have the same weight, the odds ratio can be interpreted as the odds of smokers in the sample having a low pulse being 30% of the odds of non-smokers having a low pulse. HYPOTHESIS TESTING The Wald statistic for the coefficient is: Wald (Z)= [ /s.e.B]2 which is distributed chi-square with 1 degree of freedom. The last Log-Likelihood from the maximum likelihood iterations is displayed along with the statistic G. This statistic tests the null hypothesis that all the coefficients associated with predictors equal zero versus these coefficients not all being equal to zero. In this example, G = 7.574, with a p-value of 0.023, indicating that there is sufficient evidence that at least one of the coefficients is different from zero, given that your accepted level is greater than 0.023. EVALUATING THE PERFORMANCE OF THE MODEL Goodness-of-Fit Tests displays Pearson, deviance, and Hosmer-Lemeshow goodnessof-fit tests. If the p-value is less than your accepted α-level, the test would reject the null hypothesis of an adequate fit. The goodness-of-fit tests, with p-values ranging from 0.312 to 0.724, indicate that there is insufficient evidence to claim that the model does not fit the data adequately MULTICOLLINEARITY The presence of multicollinearity will not lead to biased coefficients. But the standard errors of the coefficients will be inflated. If a variable which you think should be statistically significant is not, consult the correlation coefficients. If two variables are correlated at a rate greater than .6, .7, .8, etc. then try dropping the least theoretically important of the two.