Download Quantum Physics - StrikerPhysics

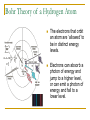
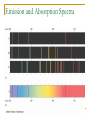
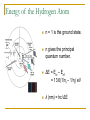
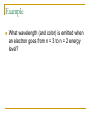
Quantum Physics
Chapter 27!
Quantum – What does that mean?

The study of light at the beginning of the last century led to unanswered
questions about the nature of light. Physicists use models to describe
phenomena they cannot see or measure directly.

The wave model of light was successful in predicting most observed
behavior, but certain observations could not be explained using a wave
model.

A new hypothesis was formed :
Light can also be modeled as a particle. light is quantized: it is
transferred only in discrete quantities of energy.

A quantum is a discrete unit of electromagnetic energy.
Wave – Particle Duality

Particles exhibit wave properties

Waves behave as particles

Both models may be used to understand the
physical world.
Quantum Mechanics

Quantum Mechanics is the branch of physics
that studies extremely small particles and
their interactions with electromagnetic
energy.

Calculations involving such small particles
deal with probabilities rather than precise
values.
Blackbody Radiation

A blackbody is a perfect absorber
of electromagnetic radiation. In
theory it absorbs ALL incident
radiation.

A box with a very small hole acts
like a blackbody because nearly all
incident radiation is absorbed.

As a perfect absorber, it is also a
perfect emitter of radiation. We
study the emissions – intensity vs.
temperature
Blackbody Radiation

At normal temperatures, radiation
is emitted in the infared region.

As temperature increases, the
object emits radiation in the
visible portion of the spectrum.

Though there is a continuous
spectrum of emission
wavelengths, the maximum
intensity occurs at a particular
wavelength.

This wavelength decreases as
temperature increases.
Wein’s Displacement Law

As temperature increases,
more radiation is emitted at
every wavelength.

Also the wavelength of max
intensity, λmax, becomes
shorter.

Wein’s Law:
λmaxT = 2.90 X 10 -3 mK
Example

The visible surface of our sun is the gaseous
photosphere from which radiation escapes.
At the top of the photosphere the temperature
is 4500 K. At a depth of 260 km the
temperature is 6800 K. What are the
wavelengths of maximum intensity for these
temperatures? What colors do they
correspond to?
Planck’s Constant –
The Ultraviolet Catastrophe!

Classical physics (Newtonian) predicts that emitted energy
depends on the frequency of the oscillating charge:
Intensity is proportional to (1/λ)4
i.e. As wavelength decreases, I increases.

Classical theory agrees for longer wavelengths, but for
shorter wavelengths (shorter than violet) experimental data
disagrees with classical physics!

Predicted intensity would grow to infinity, but
experimentally the intensity drops to zero!
Planck’s Constant –
The Ultraviolet Catastrophe!

Max Planck developed a theory that matched the experimental
evidence, but his theory relied on the premise that energy emitted
by an object can only be emitted in discrete amounts!

En = n(hf) integer multiples of hf where
h = planck’s constant = 6.63 X 10 –34 Js

The smallest amount of energy emitted by an oscillator is
E = hf.
Energy is quantized!
Photoelectric Effect

One of Einstein’s famous experiments!

Light is absorbed and emitted in discrete
quantities called photons with energy E = hf.

Einstein used the photon concept to explain
the photoelectric effect…
Photoelectric Effect

A photoelectric material is the
cathode end of a capacitor –
when light shines on it,
electrons can be liberated.

The capacitor is placed inside
an evacuated tube.

A variable voltage supply
maintains the potential across
the plates.

When electrons are liberated, a
current is measured in the
ammeter.
Photoelectrons

The energy from the light
source hitting the cathode
causes electrons to be
freed…

With a potential difference
between anode and
cathode, all ‘photoelectrons’
make it to the anode.

Current of photoelectrons
can be measured, Ip
Increasing
the voltage
does not increase Ip
Increasing
the intensity of
light DOES increase Ip.
Photoelectrons

Kinetic energy of the
photoelectrons can be
measured by making V<0.

The retarding voltage repels the
photoelectrons.

Photocurrent decreases as
voltage gets more negative;
only photoelectrons with
KE > e|V| will make it to the
anode.

The ‘stopping voltage’ gives
the max kinetic energy of the
photoelectrons
Kinetic Energy Observations

Varying the intensity changes the photoelectron
current but does NOT change the stopping voltage /
max KE.

Varying the frequency DOES affect the maximum
kinetic energy.

Max Kinetic Energy varies linearly with increasing
frequency.

There is a minimum frequency below which no
current is detected.
Photoelectric Effect
Explained by Einstein

hf = KE + Φ
f gives frequency of incident
light
h is planck’s constant
KE is measured max kinetic
energy of photoelectrons
Φ is work required to liberate
an electron

KE = hf - Φ
eV or electron-volts

Small energy quantities are measured in
electron-volts. An electron volt is the potential
energy of an electron when pushed through a
potential of 1 Volt (1 Joule/Coulomb)

1 eV = (1.6X 10 -19 C)(1 J/C) = 1.6 X 10 -19 J
Examples

The work function of a particular metal is 2.00eV. If
the metal is illuminated with light of wavelength 550
nm,
a) what is the maximum kinetic energy of the
emitted photoelectrons?
b) what is their maximum speed?
c) what is the stopping potential?
Cutoff Frequency or Threshold Frequency

Below a particular frequency, the
photoelectrons in the photoelectric material
don’t have enough energy to dislodge.

This frequency is called the cutoff frequency.

hf = KE + Φ

f0 = Φ/h gives the cutoff frequency
hf0 = 0 + Φ
Example

What are the cutoff frequency and
corresponding wavelength for the metal
described in the last example??
Compton Scattering

Arthur Compton in 1923
described the scattering
of x-rays from a carbon
block by assuming
incident radiation is a
particle or quantum.
Compton Scattering
Observations:
 When monochromatic light scatters from various materials, the
wavelength of the scattered radiation is longer.

The wavelength of the scattered radiation depended upon the
angle through which it was scattered.

The wavelength of scattered radiation did not depend on the
nature of the scattering material.

Classical physics / wave theory predicts that the scattered
radiation should have the same wavelength as the incident
radiation.
Compton Scattering

Compton assumed light behaved
as a particle.

He also assumed that light incident
on scattering material was
scattered through elastic collisions
with electrons. (Why not the
nucleus?)

For an elastic collision, momentum
and kinetic energy are conserved.

These assumptions led Compton
to a complete and accurate
description of the observed
scattering.
Compton’s Result
Δλ = λ’ – λ = λc(1 – cosθ)
λc = 2.43 X 10 -12 m
= Compton wavelength
Based on elastic collisions of
particles, Compton
derived a formula which
correctly predicts the shift
in wavelength.
Example

A monochromatic beam of x- ray radiation of
wavelength 1.35 X 10 -10 m is scattered by
the electrons in a metal foil. By what
percentage is the wavelength shifted if the
scattered x-rays are observed at 90 degrees?
Homework

Read carefully Section 27.4 – The Bohr
Theory of the Hydrogen Atom

This week: 27.4, 28.1, 29.2 – 29.4

Do # 29, 32, 36, 38, 39, 41, 45 – 47, 50
Bohr Theory of a Hydrogen Atom

The electrons that orbit
an atom are ‘allowed’ to
be in distinct energy
levels.

Electrons can absorb a
photon of energy and
jump to a higher level,
or can emit a photon of
energy and fall to a
lower level.
Emission and Absorption Spectra
Bohr’s Model

Bohr assumed electron orbits the proton in a
similar fashion to planet orbiting the sun.

He assumed the electrical force provided the
centripetal force.

He also assumed that angular momentum
was quantized! Could only exist in multiples
of h/2π
Energy of Hydrogen Atom

Centripetal force = Electrical Force
m(v2/r) = ke2/r2

(1)
Energy = KE + PE
KE = ½ mv2; PE = -ke2/r

Energy = ke2/2r - ke2/r = ke2/2r - 2ke2/2r
Energy = -ke2/2r
(2)
Energy of the Hydrogen Atom

So Far: Energy = -ke2/2r

So Far: This comes from classical considerations
of energy and circular motion.

The Leap: Neils Bohr assumed that the angular
momentum of the electron was quantized: mvr =
n(h/2π) for n = 1, 2, 3…

So vn = nh/2πmr
putting this into (1) and solving for r we get
rn = (h2/4π2ke2m)n2 n = 1, 2, 3, …
(2)
Energy of the Hydrogen Atom

rn = (h2/4π2ke2m)n2 n = 1, 2, 3, …
gives the radius of electron orbitals

Substituting into equation (2)

En = -ke2/2r
= -(2π2k2e4m/h2)(1/n2)

Hydrogen:
rn = 0.0529n2 nm
En = -13.6/n2 eV
Energy of the Hydrogen Atom

n = 1 is the ground state.

n gives the principal
quantum number.

ΔE = Eni – Enf
= 13.6(1/nf – 1/ni) eV

λ (nm) = hc/ ΔE
Example

What wavelength (and color) is emitted when
an electron goes from n = 3 to n = 2 energy
level?
Example

We know four wavelengths of the Balmer
Series are in the visible range (corresponding
to n = 2, 3, 4, 5, 6). There are more than just
these four in the series. What type of light
are they likely to be? Infared, visible or
ultraviolet? What is the longest wavelength
in the Balmer Series??
Homework

Do # 53, 55, 57, 59, 60, 62 – 67, 71 on page
875