* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Document
Renormalization wikipedia , lookup
Spectral density wikipedia , lookup
Theoretical and experimental justification for the Schrödinger equation wikipedia , lookup
Weakly-interacting massive particles wikipedia , lookup
Quantum chromodynamics wikipedia , lookup
Compact Muon Solenoid wikipedia , lookup
Mathematical formulation of the Standard Model wikipedia , lookup
Future Circular Collider wikipedia , lookup
ATLAS experiment wikipedia , lookup
Renormalization group wikipedia , lookup
Strangeness production wikipedia , lookup
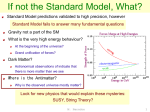
Grand Unified Theory wikipedia , lookup
Technicolor (physics) wikipedia , lookup
Minimal Supersymmetric Standard Model wikipedia , lookup
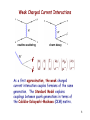
D0-D0 Mixing Michael D. Sokoloff University of Cincinnati The oscillation in time of neutral D mesons into their antiparticles, and vice versa, commonly called D0-D0 mixing, has been observed by several experiments in a variety of channels during the past year. While K0-K0 mixing and B0-B0 mixing are (relatively) well understood in the Standard Model of particle physics, the observations of D0-D0 mixing indicate that the physical eigenstates have decay rate differences and/or mass differences greater than expected most naively. In this talk I will discuss the recent experimental results and the extent to which they probe nonperturbative QCD and physics beyond the Standard Model. 1 The Nature of Particle Physics • Particle physicists study the fundamental constituents of matter and their interactions. • Our understanding of these issues is built upon certain fundmental principles – The laws of physics are the same everywhere – The laws of physics are the same at all times – The laws of physics are the same in all inertial reference systems (the special theory of relativity) – The laws of physics should describe how the wave function of a system evolves in time (quantum mechanics) • These principles do not tell us what types of fundamental particles exist, or how they interact, but they restrict the types of theories that are allowed by Nature. • In the past 30 years we have developed a Standard Model of particle phyiscs to describe the electromagnetic, weak nuclear, and strong nuclear interactions of constituents in terms of quantum field theories. In addition to the particles and forces of the Standard Model, there must be New Physics, also called Physics Beyond the Standard Model. 2 Special Relativity • Energy and Momentum – Energy and momentum form a four-vector (E,px,py,pz). The Lorentz invariant quantity defined by energy and momentum is mass: – For the special case when an object is at rest so that its momentum is zero • When a particle decays, we can measure the energy and momenta of it decay products (the daughters), albeit imperfectly. From these, we calculate the energy and momentum of the parent. From the reconstructed energy and momentum of the candidate parent, we calculate its invariant mass. 3 Classical Field Theory (E&M) 4 Fields and Quanta • • • • • Electromagnetic fields transfer energy and momentum from one charged particle to another. Electromagnetic energy/momentum is quantized: – E = hn ; p = hn/c These quanta are called photons: g In relativistic quantum field theory: Am g To calculate cross-sections and decay rates we use perturbation theory based on Feynman Diagrams: 5 Strong Nuclear Interactions of Quarks and Gluons Each quark carries one of three strong charges, and each antiquark carries an anticharge. For convenience, we call these colors: Just as photons are the quanta of EM fields, gluons are the quanta of strong nuclear fields; however, while photons are electrically neutral, gluons carry color-anticolor quantum numbers. The Nobel Prize in Physics 2004 Gross Politzer Wilczek 6 Baryons and Mesons • Quarks are never observed as free particles. – Baryons consist of three quarks, each with a different color (strong nuclear) charge proton = neutron = – Mesons consist of quark-antiquark pairs with canceling color-anticolor charges • Baryons and meson (collectively known as hadrons) have net color charge zero. • A Van der Waals-types of strong interaction creates an attractive force which extends a short distance (~ 1 fm) to bind nucleii together. 7 Weak Charged Current Interactions neutrino scattering charm decay f ~ f As a first approximation, the weak charged current interaction couples fermions of the same generation. The Standard Model explains couplings between quark generations in terms of the Cabibbo-Kobayashi-Maskawa (CKM) matirx. 8 Weak Phases in the Standard Model b = f1; a = f2; g = f3 9 Charm Meson Mixing Why is observing charm mixing interesting? It completes the picture of quark mixing already seen in the K, Bd, and Bs systems. K — PR 103, 1901 (1956); PR 103, 1904 (1956). Bd — PL B186, 247 (1987); PL B192, 245 (1987). Bs — PRL 97, 021802 (2006); PRL 97, 242003 (2006). In the Standard Model, it relates to processes with downtype quarks in the mixing loop diagram. It is a significant step toward observation of CP violation in the charm sector. It could indicate new physics. 10 Mixing Phenomenology Neutral D mesons are produced as flavor eigenstates D0 and D0 and decay via D1, D2 have masses M1, M2 and widths 1, 2 Mixing occurs when there is a non-zero mass or lifetime difference as mass, lifetime eigenstates D1, D2 where and For convenience define, x and y where and define the mixing rate ( < 5 x 10-4 ) 11 How Mixing is Calculated 12 Standard Model Mixing Predictions Box diagram SM charm mixing rate naively expected to be very low (RM~10-10) (Datta & Kumbhakar) Z.Phys. C27, 515 (1985) CKM suppression → |VubV*cb|2 GIM suppression → (m2s-m2d)/m2W Di-penguin mixing, RM~10-10 Phys. Rev. D 56, 1685 (1997) Enhanced rate SM calculations generally due to long-distance contributions: first discussion, L. Wolfenstein Phys. Lett. B 164, 170 (1985) 13 Standard Model Mixing Predictions Box diagram SM charm mixing rate naively expected to be very low (RM~10-10) (Datta & Kumbhakar) Z.Phys. C27, 515 (1985) CKM suppression → |VubV*cb|2 GIM suppression → (m2s-m2d)/m2W Di-penguin mixing, RM~10-10 Phys. Rev. D 56, 1685 (1997) Enhanced rate SM calculations generally due to long-distance contributions: first discussion, L. Wolfenstein Phys. Lett. B 164, 170 (1985) Partial History of LongDistance Calculations • Early SM calculations indicated long distance contributions produce x<<10-2: – x~10-3 (dispersive sector) • PRD 33, 179 (1986) – x~10-5 (HQET) • Phys. Lett. B 297, 353 (1992) • Nucl. Phys. B403, 605 (1993) • More recent SM predictions can accommodate x, y ~1% [of opposite sign] (Falk et al.) – x,y ≈ sin2 qC x [SU(3) breaking]2 • Phys.Rev. D 65, 054034 (2002) • Phys.Rev. D 69, 114021 (2004) 14 New Physics Mixing Predictions Possible enhancements to mixing due to • Large possible SM contributions to new particles and interactions in new mixing require observation of either a physics models CP-violating signal or | x | >> | y | to Most new physics predictions for x establish presence of NP Extended Higgs, tree-level FCNC • A recent survey (arXiv:0705.365v1) Fourth generation down-type quarks summarizes models and constraints: Supersymmetry: gluinos, squarks Lepto-quarks Fourth generation Vector leptoquarks Q = -1/3 singlet quark Flavor-conserving Two-Higgs Q = +2/3 singlet quark Flavor-changing neutral Higgs Little Higgs Scalar leptoquarks Generic Z’ MSSM Left-right symmetric Heavy weak iso-singlet quarks Supersymmetric alignment and more 15 Time-Evolution of D0K Decays RS = CF DCS and mixing amplitudes interfere to give a “quadratic” WS decay rate (x, y << 1): WS = DCS DCS K+- D0 D0 where and is the phase difference between DCS and CF decays. 16 D0 K Reconstruction 384 fb-1 e+e- c,c Slow pion charge tags neutral D production flavor Beam spot: x ≈ 100 mm y ≈ 7 mm 17 Full Fit Procedure Unbinned maximum likelihood fit in several steps (fitting 1+ million events takes a long time) Fit to m(K) and Dm distribution: RS and WS samples fit simultaneously Signal and some background parameters shared All parameters determined in fit to data, not MC Fit RS decay time distribution: Determines D0 lifetime and resolution function Include event-by-event decay time error t in resolution Use m(K) and Dm to separate signal/bkgd (fixed shapes) Fit WS decay time distribution: Use D0 lifetime and resolution function from RS fit Compare fit with and without mixing (and CP violation) 18 Simplified Fit Strategy & Validation Fit m(K) and Dm in bins of time: If no mixing, ratio of WS to RS signal should be constant No assumptions made on time evolution of background Each time bin is fit independently WS (0.75<t<2.5 ps) m(K+–) Time bins: WS (0.75<t<2.5 ps) Dm 19 Simplified Fit Strategy & Validation Rate of WS events clearly increases with time: WS/RS (%) (stat. only) 20 Simplified Fit Strategy & Validation Rate of WS events clearly increases with time: WS/RS (%) (stat. only) Inconsistent with no-mixing hypothesis: 2=24 21 Simplified Fit Strategy & Validation Rate of WS events clearly increases with time: WS/RS (%) (stat. only) Consistent with prediction from full likelihood fit 2=1.5 Inconsistent with no-mixing hypothesis: 2=24 22 Full Fit Procedure Unbinned maximum likelihood fit in several steps (fitting 1+ million events takes a long time) Fit to m(K) and Dm distribution: RS and WS samples fit simultaneously Signal and some background parameters shared All parameters determined in fit to data, not MC Fit RS decay time distribution: Determines D0 lifetime and resolution function Include event-by-event decay time error t in resolution Use m(K) and Dm to separate signal/bkgd (fixed shapes) Fit WS decay time distribution: Use D0 lifetime and resolution function from RS fit Compare fit with and without mixing (and CP violation) 23 m(K)-Dm Fit Results Signal = 1 141 500 ± 1 200 Signal = 4 030 ± 90 24 Full Fit Procedure Unbinned maximum likelihood fit in several steps (fitting 1+ million events takes a long time) Fit to m(K) and Dm distribution: RS and WS samples fit simultaneously Signal and some background parameters shared All parameters determined in fit to data, not MC Fit RS decay time distribution: Determines D0 lifetime and resolution function Include event-by-event decay time error t in resolution Use m(K) and Dm to separate signal/bkgd (fixed shapes) Fit WS decay time distribution: Use D0 lifetime and resolution function from RS fit Compare fit with and without mixing (and CP violation) 25 Decay Time Resolution Average D0 flight length is twice average resolution Resolution function described by sum of 3 Gaussians Resolution widths scales with t Mean of core Gaussian allowed to be non-zero Observed core Gaussian shifted 3.6±0.6fs = For combinatorial background, use Gaussians and power-law “tail” for small long-lived component 26 RS Decay Time Fit RS decay time, signal region plot signal region: 1.843<m<1.883 GeV/c2 0.1445<Dm< 0.1465 GeV/c2 D0 lifetime and resolution function fitted in RS sample: = 410.3±0.6 (stat.) fs Consistent with PDG (410.1±1.5 fs) NB: Shifted core Gaussian dominates systematic uncertainties 27 Full Fit Procedure Unbinned maximum likelihood fit in several steps (fitting 1+ million events takes a long time) Fit to m(K) and Dm distribution: RS and WS samples fit simultaneously Signal and some background parameters shared All parameters determined in fit to data, not MC Fit RS decay time distribution: Determines D0 lifetime and resolution function Include event-by-event decay time error t in resolution Use m(K) and Dm to separate signal/bkgd (fixed shapes) Fit WS decay time distribution: Use D0 lifetime and resolution function from RS fit Compare fit with and without mixing (and CP violation) 28 WS Fit with no Mixing WS decay time, signal region plot signal region: 1.843<m<1.883 GeV/c2 0.1445<Dm< 0.1465 GeV/c2 data - no mix PDF Fit result assuming no mixing: RD: (3.53±0.08±0.04)x10-3 29 WS Fit with no Mixing WS decay time, signal region plot signal region: 1.843<m<1.883 GeV/c2 0.1445<Dm< 0.1465 GeV/c2 data - no mix PDF Fit result assuming no mixing: poor fit RD: (3.53±0.08±0.04)x10-3 30 WS Fit with Mixing WS decay time, signal region plot signal region: 1.843<m<1.883 GeV/c2 0.1445<Dm< 0.1465 GeV/c2 Fit results allowing mixing: RD: (3.03±0.16±0.10)x10-3 x’2: (-0.22±0.30±0.21)x10-3 y’: (9.7±4.4±3.1)x10-3 data - no mix PDF fine fit 31 Signal Significance Significance calculated from change in log likelihood: (stat. only) Best fit 1 2 3 4 No mixing 5 32 Signal Significance Significance calculated from change in log likelihood: (stat. only) Best fit 1 Corresponds to 4.5 (with 2 parameters) 2 3 4 No mixing 5 33 Signal Significance Best fit is in unphysical region (x'2<0) (stat. only) Best fit Physical solution (y'=6.4x10-3) 1 Corresponds to 4.5 (with 2 parameters) 2 3 4 No mixing 5 34 Signal Significance with Systematics Including systematics (~ 0.7 x stat) decreases signal significance [ PRL. 98, 211802 (2007) ] Best fit 1 2 3 Fit is inconsistent with no-mixing at 3.9 No mixing 4 5 35 K Analysis from Belle Last year Belle published analysis of K decays: PRL 96,151801 Results consistent within 2: 400 fb-1 stat. only BaBar 1 BaBar 2 BaBar 3 no-mixing excluded at 2 (0,0) Belle 2 statistical 36 Average K Mixing Results Heavy flavor averaging group (HFAG) provides “official” averages Combine BaBar and Belle likelihoods in 3 dimensions (RD, x'2,y') May 2007 Averages: +0.14 RD: (3.30 -0.12 ) x 10-3 x’2: (-0.01±0.20) x 10-3 y’ : +2.8 (5.5 -3.7 )x 10-3 1 y' 2 No mixing excluded > 4 x'2 3 4 5 37 Preliminary Kπ Mixing Results from CDF Best fit for mixing parameters (uncertainties are combined stat. and systematic) • Fit 2 = 19.2 for 17 dof • 3.8 from Null Hypothesis RD: (3.04 ± 0.55 ) x 10-3 x’2: (-0.12 ± 0.35) x 10-3 y’ : (8.5 ± 7.6 ) x 10-3 38 D in D0 → h+h[ PRL. 91, 121801 (2003) ] 39 BaBar’s Early D in D0 → h+h[ PRL. 91, 121801 (2003) ] 91 fb-1 40 Belle’s Recent D in D0 → h+h[ PRL. 98, 211803 (2007) ] 540 fb-1 Ave (1.12 ± 0.32)% 41 BaBar’s Preliminary D D0 → h+h- 42 D0 → h+h- : Results Babar’s preliminary 384 fb-1 results Combining KK and results gives yCP = (1.24 ± 0.39 ± 0.13)% CP violation consistent with zero. BaBar Tagged (preliminary) (1.24 ± 0.39 ±0.13)% BaBar Untagged (91 fb-1) (0.2 ± 0.4 ± 0.5)% BaBar Combined (0.94 ± 0.35)% Belle Tagged (1.31 ± 0.32 ± 0.25)% BaBar + Belle Combined (1.10 ± 0.27)% 43 Mixing in D0 → KSπ+π- 44 Mixing in D0 → KSπ+πX : (0.80 ± 0.35 ± 0.15)% y : (0.33 ± 0.24 ± 0.14)% (assuming no CP violation) 95% CL contours 45 Mixing in D0 → K+-0 1483 ± 56 signal events “Wrong-sign” decay rate varies across the Dalitz plot: DCS term Resonance phase Interference term CF (mixed) term Phase between RS and WS Subscript D indicates dependence on position in the Dalitz plot. Yields from 384 fb-1 Bad charm Combinatorics 46 D0 → K+-0 : Results No mixing is excluded at the 99% confidence level. Stat+syst x’’: (2.39 ± 0.61 ± 0.32) % Y’’ : (-0.14 ± 0.60 ± 0.40 )% RM: (2.9 ± 1.6) x 10-4 68.3% 95.0% 99.0% 99.9% 47 20 Years Ago 48 10 Years Ago RM < 0.92% , no int. RM < 3.6%, int allowed RM < 0.50% , semi-lep RM < 0.85%, CPV allowed in int. RDCSD = (0.68 ± 0.34 ±0.07) % RDCSD = (0.68 ± 0.34 ±0.07) % y = (0.5 ± 1.5 ± syst.) % results on the way 49 Today HFAG D0 → Kπ RD: (3.30 +0.14 -0.12 ) x 10-3 x’2: (-0.01±0.20) x 10-3 +2.8 y’ : (5.5 ) x 10-3 -3.7 y' No mixing excluded > 4 x'2 CDF D 0 → K Sπ+ π- D 0 → K + π- π0 Belle Stat+syst D in D0 → h+hBaBar + Belle (1.10 ± 0.27)% 95% CL contours 68.3% 95.0% 99.0% 99.9% 50 10 Years From Now ?? My guesstimates of what we can do, assuming 100 fb-1 from LHCb and 50 ab-1 from SuperB, in units of 10-4 x y YCP Kπ h +h - KSπ+π- y’ 0.2 5 x’’ y’’ 8 8 5 5 5 K+π-π0 π-π+π0 (x’)2 7 7 BES III should be able to measure cos ± 3 III will measure SCS branching fractions with 5% SuperB and BES fractional precision, constraining Standard Model contributions to x & y. Altogether, D0-D0 mixing measurements, and measurements of CPviolation in mixing, will provide insights into physics beyond the SM that will complement direct observations made at the LHC. 51 Allowing for CP Violation CP violation could introduce different time dependences for D0 (+) and D0 (-): Three possible types of CP violation: Direct CP violation in DCS decay CP violation in mixing CP violation in interference between mixing and decay Simpler to fit D0 (+) and D0 (-) separately: CP violation if one or more “±” parameters are different 52 CPV Allowed Contours Results of fitting D0 and D0 separately: x'+2: (-0.24±0.43±0.30)x10-3 y'+: (9.8±6.4±4.5)x10-3 x'-2: (-0.20±0.41±0.29)x10-3 y'-: (9.6±6.1±4.3)x10-3 AD=(-2.1±5.2±1.5)% D0 D0 No evidence for CP violation found 53