Download Document

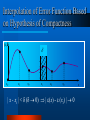
DEXA-99
10th International Conference and
Workshop on Database and Expert
Systems Applications
Mining Several Databases with
an Ensemble of Classifiers
Seppo Puuronen
Vagan Terziyan
Alexander Logvinovsky
August 30 - September 3, 1999
Florence, Italy
Authors
Seppo Puuronen
Vagan Terziyan
[email protected]
[email protected]
Department of Computer
Science and Information
Systems
University of Jyvaskyla
FINLAND
Department of Artificial
Intelligence
Kharkov State Technical
University of Radioelectronics,
UKRAINE
Alexander Logvinovsky
[email protected]
Department of Artificial Intelligence
Kharkov State Technical University of Radioelectronics,
UKRAINE
Contents








The problem of “multiclassifiers” - “multidatabase”
mining;
Case “One Database - Many Classifiers”;
Dynamic integration of classifiers;
Case “One Classifier - Many Databases”;
Weighting databases;
Case “Many Databases - Many Classifiers”;
Context-based trend within the classifiers predictions
and decontextualization;
Conclusion
Introduction
Introduction
Problem
Problem
Case ONE:ONE
Case ONE:MANY
Dynamic Integration of Classifiers

Final classification is made by weighted
voting of classifiers from the ensemble;

Weights of classifiers are recalculated for
every new instance;

Weighting is based on predicted errors of the
classifiers in the neighborhood area of the
instance
Sliding Exam of a Classifier
(Predictor, Interpolator)




Remove an instance y(xi)
from training set;
Use a classifier to derive
prediction result y’(xi);

y(x)

Evaluate difference
as
distance between real and
predicted values
Continue for every
instance
xi-1 xi xi+1 x
Brief Review of Distance Functions
According to D. Wilson and T. Martinez (1997)
PEBLS Distance Evaluation for Nominal
Values (According to Cost S. and Salzberg S., 1993 )
The distance di between two values v1 and v2 for certain
instance is:
2
k
 C1i
C2i 
d (v1 , v 2 )   

 ,
C2 
i 1  C1
where C1 and C2 are the numbers of instances in the
training set with selected values v1 and v2, C1i and C2i
are the numbers of instances from the i-th class, where
the values v1 and v2 were selected, and k is the number
of classes of instances
Interpolation of Error Function Based
on Hypothesis of Compactness
x

x0
x1
x2
xi
x3
x4
| x - xi | <  (  0)  | (x) -  (xi) |  0
x
Competence map

absolute difference


weight function


x
1
1  2
3
2
1
1
A
3
2
B
2
C
1
D
x
Solution for ONE:MANY
y
i
y
i

i
i
i
Case MANY:ONE
Integration of Databases

Final classification of an instance is obtained
by weighted voting of predictions made by the
classifier for every database separately;

Weighting is based on taking the integral of
the error function of the classifier across
every database
Integral Weight of Classifier 
(x)
DB
1
a
Classifier
xi
(x)
b
1 
2
x

b
DB
n
xi

1
x
1
j 

(
x
)
j
b  a a
Solution for MANY:ONE
 y j j
y
j

 j
j
Case MANY:MANY
Weighting Classifiers and Databases
Classifier1
DB1
y11, 11 (11)
DB2
y21, 21 (21)
…
…
DBn
yj 

i 1
m
i

 j
i 1
j 
y1m, 1m (1m)
y1, 1
…
y2m, 2m (2m)
…
y2, 2
…
ynm, nm (nm)
yn, n
ym, m
y, 
yn1, n1 (n1)
y1, 1
…
m
y ij ij
Classifier m
…
…
Prediction and weight of a database
m
…
…

Prediction and weight of a classifier
n
 ij ij
i 1
m
i

 j
i 1
yi 

n
y ij ij
j 1
n
 ij
j 1
i 
i i

 j j
j 1
n
i

 j
j 1
Solutions for MANY:MANY
Solutions for MANY:MANY
m
1
y
i i
y
 
i 1
m
i


i 1
1
3
3
2
2
y
n
y 
j
j 1
y
n

j 1
j

i, j

 ij
i, j
j
y ij ij
Decontextualization of Predictions

Sometimes actual value cannot be predicted as
weighted mean of individual predictions of classifiers
from the ensemble;
 It means that the actual value is outside the area of
predictions;
 It happens if classifiers are effected by the same type of
a context with different power;
 It results to a trend among predictions from the less
powerful context to the most powerful one;
 In this case actual value can be obtained as the result of
“decontextualization” of the individual predictions
Neighbor Context Trend
y
actual value: “ideal context”
y(xi)
prediction in (1,2,3) neighbor context:
“better context”
y+(xi)
2
y-(x )
i
1
prediction in (1,2) neighbor context:
“worse context”
xi
3
x
Main Decontextalization Formula
y-
y’
y+
y
Y
’
y+ - prediction in better context
+
y’ - decontextualized prediction
-
- ·+
’ =  - +  +
y- - prediction in worse context
y - actual value
+ < -
’ < - ; ’ < +
Decontextualization

One level decontextualization

All subcontexts
decontextualization

Decontextualized difference

New sample classification

y 
y   yi 
y   yi 
y  y
1
y  

.

y y
 1 
1
   j  

y
j  y

 = y – y
y(x) = y(x)+ (x)
Physical Interpretation of
Decontextualization
predicted values
actual value
R1
yi- - prediction in worse context
y+ - prediction in better context
y’ - decontextualized prediction
R2
y-
y+
y’
actual value
y
y
y - actual value
decontextualized value
Rres
R1  R2
Rres 
R1  R2
Uncertainty is like a “resistance”
for precise prediction
Conclusion




Dynamic integration of classifiers based on locally
adaptive weights of classifiers allows to handle the case
«One Dataset - Many Classifiers»;
Integration of databases based on their integral weights
relatively to the classification accuracy allows to handle
the case «One Classifier - Many Datasets»;
Successive or parallel application of the two abowe
algorithms allows a variety of solutions for the case
«Many Classifiers - Many Datasets»;
Decontextualization as the opposite to weighted voting
way of integration of classifiers allows to handle context
of classification in the case of a trend