* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Document
Genetic algorithm wikipedia , lookup
Neuromancer wikipedia , lookup
Existential risk from artificial general intelligence wikipedia , lookup
Time series wikipedia , lookup
Narrowing of algebraic value sets wikipedia , lookup
Knowledge representation and reasoning wikipedia , lookup
Gene prediction wikipedia , lookup
Pattern recognition wikipedia , lookup
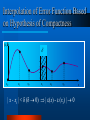
DEXA-99 10th International Conference and Workshop on Database and Expert Systems Applications Mining Several Databases with an Ensemble of Classifiers Seppo Puuronen Vagan Terziyan Alexander Logvinovsky August 30 - September 3, 1999 Florence, Italy Authors Seppo Puuronen Vagan Terziyan [email protected] [email protected] Department of Computer Science and Information Systems University of Jyvaskyla FINLAND Department of Artificial Intelligence Kharkov State Technical University of Radioelectronics, UKRAINE Alexander Logvinovsky [email protected] Department of Artificial Intelligence Kharkov State Technical University of Radioelectronics, UKRAINE Contents The problem of “multiclassifiers” - “multidatabase” mining; Case “One Database - Many Classifiers”; Dynamic integration of classifiers; Case “One Classifier - Many Databases”; Weighting databases; Case “Many Databases - Many Classifiers”; Context-based trend within the classifiers predictions and decontextualization; Conclusion Introduction Introduction Problem Problem Case ONE:ONE Case ONE:MANY Dynamic Integration of Classifiers Final classification is made by weighted voting of classifiers from the ensemble; Weights of classifiers are recalculated for every new instance; Weighting is based on predicted errors of the classifiers in the neighborhood area of the instance Sliding Exam of a Classifier (Predictor, Interpolator) Remove an instance y(xi) from training set; Use a classifier to derive prediction result y’(xi); y(x) Evaluate difference as distance between real and predicted values Continue for every instance xi-1 xi xi+1 x Brief Review of Distance Functions According to D. Wilson and T. Martinez (1997) PEBLS Distance Evaluation for Nominal Values (According to Cost S. and Salzberg S., 1993 ) The distance di between two values v1 and v2 for certain instance is: 2 k C1i C2i d (v1 , v 2 ) , C2 i 1 C1 where C1 and C2 are the numbers of instances in the training set with selected values v1 and v2, C1i and C2i are the numbers of instances from the i-th class, where the values v1 and v2 were selected, and k is the number of classes of instances Interpolation of Error Function Based on Hypothesis of Compactness x x0 x1 x2 xi x3 x4 | x - xi | < ( 0) | (x) - (xi) | 0 x Competence map absolute difference weight function x 1 1 2 3 2 1 1 A 3 2 B 2 C 1 D x Solution for ONE:MANY y i y i i i i Case MANY:ONE Integration of Databases Final classification of an instance is obtained by weighted voting of predictions made by the classifier for every database separately; Weighting is based on taking the integral of the error function of the classifier across every database Integral Weight of Classifier (x) DB 1 a Classifier xi (x) b 1 2 x b DB n xi 1 x 1 j ( x ) j b a a Solution for MANY:ONE y j j y j j j Case MANY:MANY Weighting Classifiers and Databases Classifier1 DB1 y11, 11 (11) DB2 y21, 21 (21) … … DBn yj i 1 m i j i 1 j y1m, 1m (1m) y1, 1 … y2m, 2m (2m) … y2, 2 … ynm, nm (nm) yn, n ym, m y, yn1, n1 (n1) y1, 1 … m y ij ij Classifier m … … Prediction and weight of a database m … … Prediction and weight of a classifier n ij ij i 1 m i j i 1 yi n y ij ij j 1 n ij j 1 i i i j j j 1 n i j j 1 Solutions for MANY:MANY Solutions for MANY:MANY m 1 y i i y i 1 m i i 1 1 3 3 2 2 y n y j j 1 y n j 1 j i, j ij i, j j y ij ij Decontextualization of Predictions Sometimes actual value cannot be predicted as weighted mean of individual predictions of classifiers from the ensemble; It means that the actual value is outside the area of predictions; It happens if classifiers are effected by the same type of a context with different power; It results to a trend among predictions from the less powerful context to the most powerful one; In this case actual value can be obtained as the result of “decontextualization” of the individual predictions Neighbor Context Trend y actual value: “ideal context” y(xi) prediction in (1,2,3) neighbor context: “better context” y+(xi) 2 y-(x ) i 1 prediction in (1,2) neighbor context: “worse context” xi 3 x Main Decontextalization Formula y- y’ y+ y Y ’ y+ - prediction in better context + y’ - decontextualized prediction - - ·+ ’ = - + + y- - prediction in worse context y - actual value + < - ’ < - ; ’ < + Decontextualization One level decontextualization All subcontexts decontextualization Decontextualized difference New sample classification y y yi y yi y y 1 y . y y 1 1 j y j y = y – y y(x) = y(x)+ (x) Physical Interpretation of Decontextualization predicted values actual value R1 yi- - prediction in worse context y+ - prediction in better context y’ - decontextualized prediction R2 y- y+ y’ actual value y y y - actual value decontextualized value Rres R1 R2 Rres R1 R2 Uncertainty is like a “resistance” for precise prediction Conclusion Dynamic integration of classifiers based on locally adaptive weights of classifiers allows to handle the case «One Dataset - Many Classifiers»; Integration of databases based on their integral weights relatively to the classification accuracy allows to handle the case «One Classifier - Many Datasets»; Successive or parallel application of the two abowe algorithms allows a variety of solutions for the case «Many Classifiers - Many Datasets»; Decontextualization as the opposite to weighted voting way of integration of classifiers allows to handle context of classification in the case of a trend