* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download Choosing Mesh Parameters for Complex Systems
Optical rogue waves wikipedia , lookup
Lens (optics) wikipedia , lookup
Retroreflector wikipedia , lookup
Birefringence wikipedia , lookup
Schneider Kreuznach wikipedia , lookup
Nonimaging optics wikipedia , lookup
Nonlinear optics wikipedia , lookup
Optical telescope wikipedia , lookup
Harold Hopkins (physicist) wikipedia , lookup
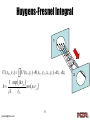
Fourier optics wikipedia , lookup
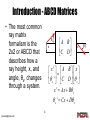
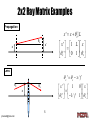
Simplified Method of Modeling Complex Systems of Simple Optics using Wave-Optics: An Engineering Approach Dr. Justin D. Mansell, Steve Coy, Liyang Xu, Anthony Seward, and Robert Praus MZA Associates Corporation 1 [email protected] Outline • Introduction – Ray Matrices – Lens Law – Fourier Optics • • • • Aperture Imaging Into Input Space Finding the Field Stop & Aperture Stop Mesh Determination for Complex Systems Conclusions 2 [email protected] Ray Matrix Formalism 3 [email protected] Introduction - ABCD Matrices • The most common ray matrix formalism is the 2x2 or ABCD that describes how a ray height, x, and angle, θx, changes through a system. θx x A B C D x' A B x ' C D x x x ' Ax B x x ' Cx D x 4 [email protected] x’ θx’ 2x2 Ray Matrix Examples Propagation θx x x ' x x L x’ x ' 1 L x ' 0 1 x x Lens x ' x x / f θx x' 1 ' 1/ f x θx’ x 5 [email protected] 0 x 1 x Example ABCD Matrices Matrix Type Propagation Lens Curved Mirror (normal incidence) Curved Dielectric Interface (normal incidence) Form Variables L = physical length n = refractive index f = effective focal length 1 L n 0 1 1 1 f 0 1 0 1 2 R 1 R = effective radius of curvature 1 0 n n R 1 2 1 n1 = starting refractive index n2 = ending refractive index R = effective radius of curvature 6 [email protected] 3x3 and 4x4 Formalisms 4x4 E = Offset F = Added Tilt 7 [email protected] A B E x C D F x 0 0 1 1 3x3 • Siegman’s Lasers book describes two other formalisms: 3x3 and 4x4 • The 3x3 formalism added the capability for tilt addition and offaxis elements. • The 4x4 formalism included two-axis operations like axis inversion and image rotation. Ax C x Bx Dx Ay Cy x x By y Dy y 5x5 Formalism Ax C x 0 0 0 • We use a 5x5 ray matrix formalism as a combination of the 2x2, 3x3, and 4x4. – Previously introduced by Paxton and Latham 8 [email protected] Bx 0 0 Dx 0 0 Ay 0 By 0 Cy Dy 0 0 0 Ex x Fx x Ey y Fy y 1 1 Lens Law • This equation governs the location of the formation of an image. 1 1 1 f d1 d 2 1 1 1 d1 f f d2 d1 d 2 f d1 fd1 d1 f f d1 M eff f d 2 d1 M eff object image f d2 9 [email protected] d1 Huygens Principle In 1678 Christian Huygens “expressed an intuitive conviction that if each point on the wavefront of a light disturbance were considered to be a new source of a secondary spherical disturbance, then the wavefront at any later instant could be found by constructing the envelope of the secondary wavelets.” -J. Goodman, Introduction to Fourier Optics (McGraw Hill, 1968), p. 31. 10 [email protected] Huygens-Fresnel Integral 1 U ( x2 , y2 ) U ( x1 , y1 ) h( x2 , y2 , x1 , y1 ) dx1 dy1 1 exp jkr21 h cosn, r21 j r21 11 [email protected] 2 Fresnel Approximation • Fresnel found that in modeling longer propagations, Huygens-Fresnel Integral U ( x2 , y2 ) U ( x1 , y1 ) h( x2 , y2 , x1 , y1 ) dx1 dy1 h – the cosine term could be neglected and – the spherical term could be approximated by a r2 term. Fresnel Approximation r2 2 exp( jkz) U ( x2 , y 2 ) exp jk jkz 2z r12 U ( x1 , y1 ) exp jk 2 z k exp j x2 x1 y2 y1 dx1 dy1 z where ra xa ya 2 12 [email protected] 1 exp jkr21 cosn, r21 j r21 2 Notation Simplification r12 Q1 exp jk 2z Quadratic Phase Factor (QPF): Equivalent to the effect a lens has on the wavefront of a field. Fourier Transform k F (U ) U exp j x2 x1 y2 y1 dx1 dy1 z exp( jkz) P Multiplicative Phase Factor: Takes into account the jkz overall phase shift due to propagation U ' P Q2 F U Q1 13 [email protected] Fresnel Approximation Validity a z 16 from Siegman 4 1/ 3 Ch.16 1/ 3 a z 4 from Goodman Ch. 4 4 spherical parabolic radius 14 [email protected] Fresnel Approximation Validity Examples a (cm) z >> (π/4 a4/λ)1/3 Goodman Nf max 100 92 m 10838 10 4.3 m 2335 1 0.2 m 503 0.1 9.2 mm 108 0.01 430 μm 23 0.001 20 μm 5 λ = 1.0 μm 15 [email protected] Implementing Fourier Propagation • One-Step Fourier Transform U ' P Q2 F U Q1 – Single Fourier integral • Convolution Propagator U ' U h dx dy – Short distances • Two Cascaded OneStep Propagations U i P Qi F U Q1 U ' P Q2 F U Qi or – Longer distances U ' P Q2 F Qi F U Q1 Qi 16 [email protected] Discrete Sample Implementation • When implementing Fourier propagation on a computer, the field is sampled at discrete points. • The mesh spacing between samples (δ) and the number of mesh points (N) required for accurate modeling are discussed later. • The mesh spacing can be different at the beginning of a propagation (δ1) than at then end (δ2) 17 [email protected] δ Samples, Not Local Area Averages • We represent the continuous wave with a series of samples, which is NOT a local average. • This can be most easily shown by Fourier transforming a 2D grid of ones. • The result is a single non-zero mesh point at the center of a mesh, but adding a guardband shows that the single non-zero mesh point is really an under-sampled sine function 1 Input FFT FFT w GB 0.8 0.6 0.4 0.2 0 55 60 65 Matlab Script x=1:1:128; x3=1:0.5:128.5; E = ones(1,128); E2 = fftshift(fft(fftshift(E))); E3 = fftshift(fft(fftshift(addGuardBand(E',1)))); figure; plot(x,E./max(E),'-o'); hold on; plot(x3,abs(E3)./max(abs(E3)),'g*-'); plot(x,E2./max(E2),'rx-'); zoomOut(0.1); 18 [email protected] 70 75 One-Step Fourier Propagator • Steps: U ' P Q2 F U Q1 – Multiply by QPF – Fourier Transform – Multiply by QPF & Phase Factor • Comments z 2 1 – Least computationally expensive – Offers no control over the resulting mesh spacing 19 [email protected] Convolution Propagator • Steps: – Fourier transform – multiplication by the Fourier transformed kernel – an inverse Fourier transform • Advantage: U 2 P U1 h dx1 dy1 F (h) H exp jz f x f y U 2 P F 1 F h F U1 P F 1 H F U1 – Maintains the mesh spacing 2 1 20 [email protected] k x2 x1 2 y2 y1 2 h exp j 2z 2 2 Two-Step Forward Propagator z z1 z 2 • Steps: – Fourier Propagate – Fourier Propagate z1 z 2 i , 2 1 i • Comments: – Easy to scale the mesh by picking intermediate plane location. – Works well in long propagation cases because the quadratic phase factor is applied before the Fourier transform z2 2 1 z1 δ1 δi z1 21 [email protected] δ2 z2 Scaling with the Convolution Propagator • One drawback of the convolution propagator is its apparent inability to scale the mesh spacing in a propagation. • Scaling the mesh is important when propagating with significant wavefront curvature. • The convolution propagator can be modified to model propagation relative to a spherical reference wavefront curvature such that the mesh spacing can follow the curvature of the wavefront. • We call this Spherical-Reference Wave Propagation or SWP. 22 [email protected] Spherical Reference Wave Propagation 1/3 • • • • Consider convolution propagation with a built in wavefront curvature relative to the lens law. Based on imaging, light propagated through an ideal lens to a distance d1 will be the same shape as if it were propagated to a distance d2 where f-1=d1-1+d2-1 except for a magnification term. For example: a beam propagating 48 cm toward a focus through a 50cm lens. Based on the lens law, this is equivalent to propagating a 1200 cm without going through the focus. It is significantly easier to propagate 1200 cm than it is to propagate 48cm. object f d2 d1 1 1 1 d 2 f d1 1 1 1 d2 1200cm 50cm 48cm 23 [email protected] image Spherical Reference Wave Propagation 2/3 • The real advantage of SWP is the ability to scale the mesh to track the evolution of the beam size. • The spherical reference wave radius of curvature (Rref) can be determined based on the desired magnification (M). δ1 z Rref 1 Rref Rref 24 [email protected] δ2 2 2 ,M Rref z 1 1 z z 1 2 1 M Spherical Reference Wave Propagation 3/3 • Procedure: – Specify desired magnification (M) and propagation distance (z) – Calculate effective reference curvature (Rref) – Determine new effective propagation distance (zeff) – Propagate the effective distance and then change the sample spacing by the magnification factor 25 [email protected] 2 M 1 Rref z 1 M 1 zeff Rref z 1 1 Mathematical Comparison of Convolution & Double Propagation Convolution Propagator with SWP Double Propagator U 2 P F 1 F h F U1 F 1 H F U1 H Qh U 2 P F 1 Qh F U1 U 2 P Q2 F Qi F U Q1 Qi If we are propagatin g relative to a We can combine the Qi terms to spherical reference, Q r , this becomes : become : U 2 P Q2 F Q2i F U Q1 U 2 P Qr 2 F 1 Qh F U1 Qr1 With the SWP addition, the Double Propagator and the Convolution Propagator are equivalent. 26 [email protected] Conclusions • We use the convolution propagator in WaveTrain with spherical-reference wave propagation. • This allows us to solve any general waveoptics problem. 27 [email protected] Computer Modeling of Fourier Propagation 28 [email protected] Computer Fourier Propagation Modeling 3 2 Phase (radians) • In most situations, the most rapidly varying part of the field is the QPF. • In a complex field, the phase is reset every wavelength or 2π radians. • To achieve proper sampling, sampling theory dictates that we need two samples per wave. 1 0 -1 -2 -3 10 20 30 40 50 60 70 Samples Inadequate Sampling Adequate Sampling k = 1; R = 16; x = -63:1:64; p = exp(j*k* (x.^2) ./ (2*R)); plot(angle(p),'b*-') 29 [email protected] Methods of Determining Sampling • Diffraction Limit • Angular Bandwidth 30 [email protected] Mesh Sampling: Whittaker-Shannon Theory • We need 2 samples for each wave of amplitude. • For a parabolic phase surface, this is most limiting at the edge of the phase surface. 31 [email protected] λ 2δ Mesh Sampling: Diffraction • Diffraction is the fundamental limit of our ability to model propagation. • If we assume we need 2 samples per diffraction spot radius on BOTH sides of a propagation, we get a maximum value for the mesh spacing. 32 [email protected] z D1 rspot D2 f 2 Dbeam z z 2 and 1 2 D1 2 D2 Mesh Sampling: Angular Bandwidth z max 2 D1 z max 1 D1 D1 z 2 2 D2 z 21 z 2 2 D1 z 1 2 D2 33 [email protected] D2 z D2 Virtual Adjacent Apertures • Now that we know the mesh sampling intervals (δ1 and δ2), we need to know how big a mesh we need to use to accurately model the diffraction. • The Fourier transform assumes a repeating function at the input. – This means that there are effective virtual apertures on all sides of the input aperture. • We need a mesh large enough that these virtual adjacent apertures do not illuminate our area of interest. 34 [email protected] Mesh Size: Equal Sized Apertures z • To avoid adjacent apertures (Dup and Ddown) Dup from interfering with the output area of interest, the modeled region should be D+θz in diameter. D D D+θz • This means that the number of mesh points should be this diameter divided by the mesh Ddown spacing (δ). • For equal apertures, this D means a factor of two z 2 D z D D 2 guard-band. N 2 4 assuming max z 2 D 35 [email protected] z Unequal Apertures • For unequal apertures (such as spherical-reference wave propagation), the same geometric argument can be made. • The resulting form can be thought of as the average of the number of mesh points required to cover each of the input apertures plus a diffractive term. • If we set the two mesh spacings to their maximum value, the number of mesh points reduces to a familiar form: General form : D1 D2 z N 21 2 2 21 2 Minimizing N ( ' s at maximum) : D1 D2 N 4 z – the Fresnel number. 36 [email protected] Fresnel Number z 2 • The Fresnel number is 2a – the number of half waves of phase of a parabolic wavefront over the aperture. – half the number of (a) a 2 r2 Nf (r ) diffraction limited 2 z 2z spots diameters over the aperture. Daperture – roughly the number of a2 a 2a Nf diffraction ripples z z a 4 z 2 Dspot across an aperture. D 37 [email protected] Mesh Size and Fresnel Number • For equal sized apertures, the number of mesh points equals 16 times the Fresnel number. • For unequal apertures, the same is true if we define an effective Fresnel number as r2r1/λz. Equal Sized Apertures Minimizing N ( ' s at maximum) : D2 r2 N 4 16 16 N f z z where N f is the Fresnel number Unequal Sized Apertures Minimizing N ( ' s at maximum) : D1 D2 r1r2 N 4 16 16 N f _ eff z z where N f _ eff is the effective Fresnel number 38 [email protected] Summary of Mesh Determination Mesh Size Mesh Sample Spacing z z 2 and 1 2 D1 2 D2 r1r2 N 16 N f _ eff 16 z for maximum 1 and 2 • Derived by either: • Derived based on eliminating overlap between adjacent virtual apertures and the region of interest. – Diffraction limit OR – Required angular bandwidth 39 [email protected] Conclusions • For a simple system of two limiting apertures, we have determined a set of inequalities that govern the choice of the mesh. • Next we will look at – how phase aberrations impact the mesh choice, and – how this can be extended to a system of multiple apertures. 40 [email protected] Impact of Phase Aberrations on Mesh Determination 41 [email protected] Sinusoidal Phase Grating sin N m 42 [email protected] Turbulence-Induced Aperture Blurring • Turbulence acts to increase the size of the point spread function • This effectively blurs the apertures at each end. • The blurred apertures can be thought of as being larger if we want to capture most of the energy. 43 [email protected] Gaussian PSF Blurred Aperture Blur Effect on Aperture Size • Turbulence can be thought Blurred Edge of a Hard Aperture of as diffracting light as if it 1 were sent through a grating with a period equal to r0, which is Fried’s coherence 0.5 length. – r0 can be though of as the characteristic turbule size. • A scaling parameter, cturb, is used to control the amount of energy captured in the calculation. – cturb ≈ 4 is for 99% of the energy. 44 [email protected] 0 180 190 200 210 Deffective Dinitial cturb r0 Procedure to Determine the Mesh while Considering Turbulence z D1’ D1 D2 1. Simplify the turbulence distribution along the path into effective r0 values for each effective aperture. 2. Modify the aperture size using the effective r0. 3. Use the new effective aperture sizes to determine the mesh. 45 [email protected] D2’ Determining Fourier Propagation Mesh Parameters for Complex Optical Systems of Simple Optics 46 [email protected] Introduction • The determination of mesh parameters for wave-optics modeling can be uniquely determined by a pair of limiting apertures separated by a finite distance. • An optical system comprised of a set of ideal optics can be analyzed to determine the two limiting apertures that most restrict rays propagating through the system using field and aperture stop techniques. 47 [email protected] Definitions of Field & Aperture Stop • Aperture Stop = the aperture in a system that limits the cone of energy from a point on the optical axis. • Field Stop = the aperture that limits the angular extent of the light going through the system. • NOTE: All this analysis takes place in rayoptics space. 48 [email protected] Example System Optical System D=15 D=1 f=100 D=5 f=100 A1 L1 150 L2 200 Input Input Space D=15 Plane 2 50 Plane 3 15 15 5 1 -50 0 A1 150 A2 L1 L2 49 [email protected] A2 Plane 4 Procedure for Finding Stops 1/3 1. Find the location and size of each aperture in input space. 1. Find the ABCD matrix from the input of the system to each optic in the system. Solve for the distance (zimage) required to drive the B term to zero by inverting the input-space to aperture ray matrix. 2. • 3. This matrix is the mapping from the aperture back to input space. The A term is the magnification (Mimage)of the image of that aperture. 50 [email protected] Mi M 1 input space _ to _ aperture Ai Ci Bi Di 0 1 zimage Ai Bi M 0 C D C 1 / M 1 i i zimage B D M image C zimage A Procedure for Finding Stops 2/3 2. Find the angle formed by the edges of each of the apertures and a point in the middle of the object/input plane. The aperture which creates the smallest angle is the image of the aperture stop or the entrance pupil. 15 15 5 1 -50 0 A1 150 A2 L2 [email protected] 51 L1 Procedure for Finding Stops 3/3 2. Find the aperture which most limits the angle from a point in the center of the image of the aperture stop in input space. This aperture is the field stop. 15 15 5 1 -50 0 A1 150 A2 L2 [email protected] 52 L1 Example: Fourier Propagation Input Space 15 15 5 1 -50 0 A1 150 A2 L1 L2 D1 = 1 mm, D2 = 15 mm, λ = 1 μm, z = 0.15 m Minimal Mesh = 400 x 9.375 μm = 3.75 mm 53 [email protected] Example System Optical System D=15 D=1 f=100 D=5 f=100 A1 L1 150 Input L2 200 Plane 2 54 [email protected] D=15 A2 50 Plane 3 Plane 4 N=1024, δ=6.6 μm Over-Sampled Input Plane 2 Plane 3 Plane 4 55 [email protected] N=512, δ=9.4 μm Minimal Sampling Input Plane 2 Plane 3 Plane 4 56 [email protected] N=256, δ=13.3 μm Under Sampled Input Plane 2 Plane 3 Plane 4 57 [email protected] Conclusions of Complex System Mesh Parameter Determination • We have devised a procedure to reduce a complex system comprised of simple optics into a pair of the most restricting apertures. • It would be nice to have a way of simplifying a complex system of simple optics so that modeling it is computationally easier… 58 [email protected] ABCD Ray Matrix Wave-Optics Propagator 59 [email protected] Implementation Options U 2 x2 , y2 exp( jkL) j B • Siegman combined the ABCD terms Ax y jk directly in the U x , y exp 2B 2x x y y dx dy Huygens integral. D x y • He then also introduced a way of A B 1 0 M 2 0 C D 1 / f 1 0 1 / M decomposing any 2 2 ABCD propagation 1 L M 1 0 1 0 0 1 0 1 / M 1 / f 1 into 5 individual 1 1 steps. 2 1 1 1 1 [email protected] 1 2 2 2 60 1 1 2 2 2 2 1 1 Polishing the Siegman Decomposition Algorithm • We found that one of the magnification terms was unnecessary (M1=1.0). • Siegman’s algorithm did not address two important situations: image planes and focal planes. • We worked a bit more on how to pick an appropriate magnification when considering diffraction. 61 [email protected] 0 A B 1 C D 1 / f 1 2 0 0 1 L 1 M 0 1 / M 0 1 1 / f 1 1 M 1 / Mf 0 1 / M L D2 AD1 2 D1 Siegman Decomposition Algorithm • Choose magnifications M1 & M2 (M=M1*M2) • Calculate the effective propagation length and the focal lengths. 62 [email protected] A B C D L B Leq 2 M M1 B f1 MA B f2 1/ M D Eliminating a Magnification Term • We determined that A B 1 0 M 2 C D 1 / f 1 0 2 one of the two magnification terms 1 L M 1 0 1 0 1 0 1 / M 1 1 / f1 that Siegman put into his decomposition was A B 1 0 C D 1 / f 1 unnecessary. 2 – There were five unknowns and four inputs. 0 1 0 0 1 L 1 M 0 1 / M 0 1 1 / f 1 1 63 [email protected] 0 1/ M 2 Image Plane: B=0 • This case is an 1 image plane. 1 / f 2 • There is no propagation involved here, but there is – curvature and – magnification. Siegman B Leq 0 M B f1 0 MA B f2 0 1/ M D 64 [email protected] 0 M 0 0 M 1 0 1 / M M / f 2 1 / M Our Algorithm Leq 0 C -1/Mf 2 1 f2 MC Focal Plane Case • We were trying to automate the selection of the magnification by setting it equal to the A term of the ABCD matrix. 1 0 0 0 1 1 / f Siegman, M=A M A0 – This minimizes the mesh requriements f M f f f1 M A 0 f f2 0 1 Leq • In doing so, we found that the decomposition algorithm was problematic at a focal plane. 65 [email protected] f 1 1 1 / f f 1 Propagation to a Focus: A=0 1 0 f 1 1 1 / f • For a collimated beam going to a focus, this ray envelope diameter is zero. • To handle this case, we augmented the magnification determination with diffraction. 0 0 1 1 / f Siegman, M=A Siegman, M=1 M A0 M 1 f M f f f1 M A 0 f f2 0 1 B f M B f1 f M A B f2 0 1/ M D Leq 66 [email protected] f 1 Leq Choosing Magnification while Considering Diffraction • We propose here to add a diffraction term to the magnification to avoid the case of M=0. • We added a tuning parameter, η, which is the number of effective diffraction limited diameters. • We leave the selection of magnification to the user. L D2 AD1 2 D1 D2 L M A 2 2 D1 D1 A 67 [email protected] 1 2 Nf Common Diffraction Patterns Airy Normalized Intensity Sinc Gaussian Normalized Radius 68 [email protected] Integrated Energy Integrated Energy Threshold = 10-10 Airy Sinc Gaussian η 69 [email protected] We concluded that η=5 is sufficient to capture more than 99% of the 1D integrated energy. Modified Decomposition Algorithm LM M f 1 LM 1 M f1 f 2 Mf1 f 2 for M1 1.0 • If at an image plane (B=0) M=A (possible need for interpolation) Apply focus • Else Leq Specify M, considering diffraction if necessary Calculate and apply the effective propagation length and the focal lengths. L B 2 M M1 B f1 MA B f2 1/ M D 70 [email protected] LM 1 LM M f 2 Implementing Negative Magnification • After going through a focus, the magnification is negated. • We implement negative magnification by inverting the field in one or both axes. – We consider the dual axis ray matrix propagation using the 5x5 ray matrix formalism. 71 [email protected] Dual Axis Implementation • In our implementation, we handle the case of cylindrical telescopes along the axes by dividing the convolution kernel into separate parts for the two axes. U 2 P F 1 H F U1 H exp jz 72 [email protected] fx zy f y 2 x 2 Example: ABCD Propagator 73 [email protected] Example System f/2 D f 2f 2f 74 [email protected] Magnitude z=2f before lens z=2f after lens z=2.5f z=3f z=3.5f z=4f 75 [email protected] Unwrapped Phase z=2f before lens z=2f after lens z=2.5f z=3f z=3.5f z=4f 76 [email protected] ABCD Ray Matrix Fourier Propagation Conclusions • We have modified Siegman’s ABCD decomposition algorithm to include several special cases, including: – Image planes – Propagation to a focus • This enables complex systems comprised of simple optical elements to be modeled in 4 steps. 77 [email protected] Questions? [email protected] (505) 245-9970 x122 78 [email protected]