* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Introduction to Lattice Dynamics
Work hardening wikipedia , lookup
History of metamaterials wikipedia , lookup
Energy applications of nanotechnology wikipedia , lookup
Colloidal crystal wikipedia , lookup
Low-energy electron diffraction wikipedia , lookup
Dislocation wikipedia , lookup
Bose–Einstein condensate wikipedia , lookup
Strengthening mechanisms of materials wikipedia , lookup
Spinodal decomposition wikipedia , lookup
Electronic band structure wikipedia , lookup
Acoustic metamaterial wikipedia , lookup
Crystal structure wikipedia , lookup
Sound amplification by stimulated emission of radiation wikipedia , lookup
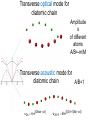
Lattice Dynamics related to movement of atoms about their equilibrium positions determined by electronic structure Physical properties of solids •Sound velocity •Thermal properties: -specific heat -thermal expansion -thermal conductivity (for semiconductors) •Hardness of perfect single crystals (without defects) Uniform Solid Material There is energy associated with the vibrations of atoms. They are tied together with bonds, so they can't vibrate independently. (X-1) The vibrations take the form of collective modes which propagate through the material. (X) (X+1) Wave-Particle Duality Just as light is a wave motion that is considered as composed of particles called photons, we can think of the normal modes of vibration in a solid as being particle-like. Quantum of lattice vibration is called the phonon. Phonon: A Lump of Vibrational Energy Propagating lattice vibrations can be considered to be sound waves, and their propagation speed is the speed of sound in the material. Roughly how big is ? Phonon: Sound Wavepackets Reminder to the physics of oscillations and waves Harmonic oscillator in classical mechanics Equation of motion: Hooke’s law m x Fspring Example: vertical springs x K ~ m x K x 0 or ~ x 0 m where x( t ) Re(~ x( t )) ~ x ( t ) A ei t Solution with ~ x(t ) A cos(t ) where K m Kx X E pot X=A sin ωt 1 2 Kx 2 x K m Displacement as a function of time and k Traveling plane waves: Y or y(t ) A cos (t kx ) ~ i( t kx ) ~ y( t ) A e 0 in particular y(t ) A cos (t kx ) 0 X (Phonon wave vector also often given as q instead of k) Consider a particular state of oscillation Y=const traveling along ~ ~ y( t ) A e solves wave equation i( t kx ) 1 2y 2y v t 2 2 x 2 d t kx d const. 0 dt dt 2 v x v k 2 / Transverse wave Longitudinal wave Standing wave ~ ~ y1 A ei(kx t ) ~ ~ y 2 A ei(kx t ) ~ ~ ys ~ y1 ~ y 2 A ei(kx t ) ei(kx t ) ~ ~ A eikx eit e it 2A eikx cos t ys Re( ys ) 2 A cos kx cost Large wavelength λ k 2 0 λ>10-8m 10-10m 8 Crystal can be viewed as a continuous medium: good for 10 m Speed of longitudinal wave: v (ignoring anisotropy of the crystal) Bs where Bs: bulk modulus with 1 2 Bs determines elastic deformation energy density U Bs2 (click for details in thermodynamic context) dilation compressibility V V E.g.: Steel v Bs Bs=160 109N/m2 ρ=7860kg/m3 v 160 109 N / m2 7860 kg / m3 1 Bs 4512 m s > interatomic spacing continuum approach fails In addition: vibrational modes quantized phonons Vibrational Modes of a Monatomic Lattice Linear chain: Remember: two coupled harmonic oscillators Symmetric mode Anti-symmetric mode Superposition of normal modes generalization Infinite linear chain How to derive the equation of motion in the harmonic approximation n-2 K un-2 n-1 a un-1 n n+1 un un+1 n+2 un+2 Fnr K un un 1 Fnl K un u n 1 un-2 un-1 un fixed un+1 un+2 ? Total force driving atom n back to equilibrium Fn K un un1 K un un1 n n K un1 un1 2un n Fn mu equation of motion K un un 1 un 1 2un m Old solution for continuous wave equation was u A ei(kx t ) . Use similar? approach for linear chain un A ei(kna t ) n 2A ei(kna t ) , u K ika ika e e 2 m 2 un1 A ei(kna t )eika 2 2 K 1 cos ka m ? , Let us try! un1 A ei(kna t )eika K 2 sin( ka / 2) m 2 K sin( ka / 2) m 2 K m Note: here pictures of transversal waves although calculation for the longitudinal case k Continuum limit of acoustic waves: sin ka / 2 ka / 2 ... k 2 0 K ak m k v K a m Technically, only have longitudinal modes in 1D (but transverse easier to see what’s happening) x = na un un (a) Chain of atoms in the absence of vibrations. (b) Coupled atomic vibrations generate a traveling longitudinal (L) wave along x. Atomic displacements (un) are parallel to x. (c) A transverse (T) wave traveling along x. Atomic displacements (un) are perpendicular to the x axis. (b) and (c) are snapshots at one instant. k k h 2 , here h=1 a k 2 i (( k h ) na t ) na (k)t ) i ( k a un A e A ei(k na t ) A e A ei(k na t )ei2 h n A ei(k na t ) (k ) (k ) k k h 2 a un(k, (k)) un(k, (k)) 1-dim. reciprocal lattice vector Gh Region k a a ei2 h n 1 is called first Brillouin zone Vibrational Spectrum for structures with 2 or more atoms/primitive basis Linear diatomic chain: 2n-2 K 2n-1 a 2n 2n+1 2n+2 2a u2n-2 u2n u2n-1 u2n+1 K u2n1 u2n1 2u2n m Equation of motion for atoms on even positions: u2 n Equation of motion for atoms on odd positions: u2 n 1 i( 2kna t ) Solution with: u2n A e and u2n+2 K u2 n 2 u2 n 2u2 n1 M u2n1 B ei(( 2n1)ka t ) A 2 K K A2 2 2 B cos ka m m K B(eika e ika ) 2 A m K B A(eika e ika ) 2 B M 2 K2 K 2 K 2 2 2 m 2 M 4 Mm cos ka 2 4 2 K B cos ka m K 2 2 m K K B 2 2 2 A cos ka M M •Click on the picture to start the animation M->m note wrong axis inKthe movie 1 1 2 2K m m M 2 K K K K 2 2 2 2 4 4 cos 2 ka Mm M m Mm K K 2 m M 4 A2 2 K M K2 1 cos 2 ka 0 4 Mm 2 2 sin2 ka k : 2a 1 1 1 1 D D m M m M 2 2 2 1 1 1 1 4 sin ka 2 K K Mm m M m M 2 K , m 2 K M 2 Transverse optical mode for diatomic chain Amplitude s of different atoms A/B=-m/M Transverse acoustic mode for diatomic chain A/B=1 u2n A ei( 2kna t ) u2n1 B ei(( 2n1)ka t ) Analogy with classical mechanical pendulums attached by spring Amplitude of vibration is strongly exaggerated! Longitudinal Eigenmodes in 1D What if the atoms were opposite charged? Optical Mode: These atoms, if oppositely charged, would form an oscillating dipole which would couple to optical fields with λ~a Summary: What is phonon? • Consider the regular lattice of atoms in a uniform solid material. • There should be energy associated with the vibrations of these atoms. • But they are tied together with bonds, so they can't vibrate independently. • The vibrations take the form of collective modes which propagate through the material. • Such propagating lattice vibrations can be considered to be sound waves. • And their propagation speed is the speed of sound in the material.