Download VII-3

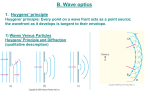
VII–3 Introduction into Wave
Optics
13. 8. 2003
1
Main Topics
• Huygens’ Principle and Coherence.
• Interference
• Double Slit
• Thin Film
• Diffraction
•
•
•
•
Single Slit
Gratings
X-Rays, Bragg Equation.
Wave Limits of Geometrical Optics.
13. 8. 2003
2
Huygens’ Principle I
• Up to now, we have have treated situations,
where many of wave properties could be
neglected. In our rays model, we actually
needed only their straight propagation.
• Now, we shall concentrate to typically wave
properties of light, which are generally valid
for all electromagnetic (and other) waves.
13. 8. 2003
3
Huygens’ Principle II
• The basis for studying wave effects is Huygens’
(Christian 1629-1695 Dutch) principle of wave
propagation. It states:
• Every point reached by a wave can be considered
as a new source of tiny wavelets that spread out in
all directions at the speed of the wave itself.
• The new wave is superposition of all the wavelets,
which usually cancel in other direction then the
wave front, which is their envelope, propagate.
13. 8. 2003
4
Huygens’ Principle III
• If light is traveling through homogeneous isotropic
media without obstacles Huygens’ principle gives
us the same results as ray (geometrical) optics
including effects as reflection and refraction.
• However, when there is e.g. an obstacle then wave
fronts will be not only distorted but new effects of
interference and diffraction will appear. There will
be for instance bright or light or colored regions
even where shadow should be.
13. 8. 2003
5
Coherence I
• Typical wave properties are based on the
principle of superposition. If several waves
meet in one spot their common effect is the
sum of all of them. But since waves are
periodic, extremes may happen e.g. they are
in phase and they will constructively
interfere or they may be out of phase and
they will interfere destructively.
13. 8. 2003
6
Coherence II
• Since the frequency of light is very high this
adding of waves may have some stable
result only if the interfering waves are
coherent i.e. have constant phase difference.
In the case of e.g. radio waves we can, in
principle build two same oscillators and
synchronize them. But electronic oscillators
for visible light don’t exist. Light can be
generated only by transitions in atoms.
13. 8. 2003
7
Coherence III
• It’s problem of accuracy and the fact that light is
not continuous, in short time scale, but comes in
‘trains’.
• So ideally coherent light waves must stem from
the same transition of the same atom.
• But also a partial coherence exists under much less
strict conditions. Diffraction can be for instance
obtained from a Sun light when it passes through a
very small aperture.
13. 8. 2003
8
Double-Slit Interference I
• This experiment was the first convincing
evidence of wave properties of light done in
1801 by Englishman Thomas Young (17731829).
• If a plane monochromatic light wave passes
through two thin, closely spaced slits. The
picture on a screen behind are not two
bright lines but rather a series of them.
13. 8. 2003
9
Double-Slit Interference II
• According to the Huygens’ principle the
slits are sources of new wavelets but now in
every point of screen only two of these
wavelets add, instead of infinity, what
would be the case without slits.
• Suppose that the distance of the slits d is
negligible to that of the screen so two rays
entering a far point of it are almost parallel.
13. 8. 2003
10
Double-Slit Interference III
• If two waves leave the slits under some
angle  their path difference is:
d = d sin
• Clearly, if d is an integral multiple of the
wavelength  the waves constructively
interfere. This condition for maxima is:
d sin = m
• m = 0, 1 … order of the interference fringe.
13. 8. 2003
11
Double-Slit Interference IV
• If, however, d is odd multiple of /2 the
waves will be completely out of phase and
they will interfere destructively. The exact
condition for minima is:
d sin = (2m+1)/2 = (m+1/2)
• Again: m = 0, 1
13. 8. 2003
12
Double-Slit Interference V
• We have found the positions of the maxima
and minima but there are also apparent
changes in intensities which we have to
explain.
• The treatment of these more subtle details is
similar to that we used in AC circuits. We
can employ the mathematics of phasors.
13. 8. 2003
13
Double-Slit Interference VI
• The intensity of light is proportional to the
square of their electric field: I ~ E2 so we
shall find the total electric field produced by
both waves at some angle , which is a sum
of fields:
E = E1 + E2
• The fields have the same  but can be phase
shifted:
E1 = E10sint and E2 = E20sin(t+)
13. 8. 2003
14
Double-Slit Interference VII
• The phase shift  can be easily related to the
path difference. From:
/2 = d sin/ 
 = 2/ d sin
• If we expect that our point on the screen is
equally illuminated by both slits we find:
E = 2E0 cos(/2)sin(t + /2)
13. 8. 2003
15
Double-Slit Interference VIII
• The same result can be found from the
phasor diagram. The phase shift of E is
clearly /2.
• We omit the fast changing term and relate
the intensity to the one in the middle, where
both waves are in phase:
I/I0 = E20 /(2E0)2 = cos2(/2)
13. 8. 2003
16
Double-Slit Interference IX
• Finally we substitute for the phase
difference :
I = I0cos2(/2) = I0cos2(dsin/)
• And for the angle  as a function of the
screen distance L and distance of the point
of interest from the center of the screen y:
y
d
2
sin    I y  I 0 [cos(
y )]
L
L
13. 8. 2003
17
Double-Slit Interference X
• y is an easy measurable variable.
• Again the same conditions for the positions
of the maxima and minima are present in
this formula but we have also obtained the
information on intensities for any point on
the screen described by  or y.
13. 8. 2003
18
Interference in Thin Films I
• The principle is the same as for any
interference generally:
• Now two waves reflected on the upper and
lower surfaces of a thin film can interfere
either constructively if the path difference in
the film is equal to integer number of
wavelengths or destructively if it is an odd
number of half wavelengths.
13. 8. 2003
19
Interference in Thin Films II
We have to consider two new effects:
• Wavelength in the particular material of the
film changes – we didn’t have to care about
this when dealing with dispersion!
• Under a certain conditions there can be
phase changes when the wave reflects.
13. 8. 2003
20
Interference in Thin Films III
• Experiments show that the waves have the
same frequency in all materials and since
the speed changes so must the wavelength:
c
v
c


f  
 n
 n 
 n
v
n
n
• If we use white light the conditions for
maximum at a certain angle will be valid
always for some color – color interference.
13. 8. 2003
21
Interference in Thin Films IV
• Experiments show important property of
reflection:
• If a wave reflects on a surface with optically
denser media it changes its phase by .
• If the second medium is less optically dense
there is no phase change.
13. 8. 2003
22
Interference in Thin Films V
• An important application of thin-film
interference is a non-reflective coating of
optical elements.
• In the case of destructive interference more
light gets through ~ 99%.
• A single layer works well for one wavelength,
usually 550 nm.
• Actually whole field of layer reflective
optics exists.
13. 8. 2003
23
Interference in Thin Films VI
• What thickness t must have a coating of
MgF2 with n = 1.38 on glass with ng = 1.5
to give destructive interference for green
light  = 550 nm?
• There will be a phase shift of /2 on the aircoating boundary and the path difference is
2t. For minima: 2t - n/2 = (2m+1) n/2 
t = n/4 = /4n = 99.6 nm
13. 8. 2003
24
Diffraction I
• Wave theory predicts that waves can be
diffracted around edges of obstacles and
interfere in the shadow behind them.
• Only after diffraction was observed the
wave nature of light was fully accepted.
• The main ideas are again based on the
Huygen’s principle.
13. 8. 2003
25
Diffraction II
• Let’s consider a diffraction pattern produced
by a single narrow slit of the width a.
• Every point in the slit is a source of
wavelets which add on some screen behind.
• Let’s find conditions for constructive and
destructive interferences:
13. 8. 2003
26
Diffraction III
• The condition for the first minimum is:
sin  = /a
• A wave from a point in the middle of the slit
has a path difference of /2 from the point
on the lower edge. These waves are out of
phase and thereby cancel themselves.
Similarly, if we proceed up, all waves will
cancel in-pairs so we get a minimum.
13. 8. 2003
27
Diffraction IV
• The condition for the first maximum is:
sin  = 3/2 /a
• If we consider points in the two adjacent thirds of
the slit, their waves will also cancel in-pairs but
the waves from points in the last third will not, so
we have a maximum intensity.
• Conditions for higher orders are found similarly.
13. 8. 2003
28
Diffraction V
• The conditions are opposite from those for
two-slit interference.
• Calculation of intensities can be again
performed using phasors.
• We can divide the slit to equivalent strips y
and find the phase difference of the waves
from adjacent strips:
 = 2/ ysin .
13. 8. 2003
29
Diffraction VI
• We are interested what will be the resulting
phasor of total field built from these small
phasors.
• In the case of minima the phasors complete
a whole circle so the total is zero.
• In other words for every phasor an opposite
phasor exists, which cancels it.
13. 8. 2003
30
Diffraction Grating I
• It’s in principle multiple parallel slits. At
present gratings can be made very precisely
with very high densities of slits of the order
of 104 lines per centimeter. Gratings can be
made both for transmission and reflection.
• The condition for principal maxima is the
same as with the double slits:
• sin = m/d here d is the adjacent spacing
13. 8. 2003
31
Diffraction Grating II
• The main difference between the double-slit
and multi-slit pattern is that the maxima in
the latter case are much sharper and
narrower.
• For a high maximum we need that waves
even from far slits are exactly in-phase. If
there is even a slight difference waves will
cancel in pairs with some those from distant
slits.
13. 8. 2003
32
Diffraction Grating III
• Gratings can be used to decompose light.
Spectrometers using gratings are actually
better than those using dispersive elements.
The resolution of gratings is higher and the
response is linear.
• This has a great impact in spectroscopy.
13. 8. 2003
33
X-Ray Diffraction I
• If we use X-rays which are EMW with the
wavelengths of the order of 10-10 m then
actually crystal planes can serve as gratings
with single atoms as single slits.
• The refractive index for these wavelengths
is almost 1 so the condition for maxima can
be described by a simple Bragg’s equation
2dsin = m
13. 8. 2003
34
X-Ray Diffraction II
• Beside positions of maxima, there is also
much information in intensities which are
interpreted by more complicated dynamical
theory.
• Methods based on X-ray diffraction are
important for characterization of structure
of materials. Different methods exist for
monocrystals, powders or even solutions.
13. 8. 2003
35
Polarization I
• In unpolarized light the electric vectors
have random position in the plane
perpendicular to the propagation of the
wave.
• It is however possible to polarize light i.e.
to select electric vectors only in a certain
plane. This is done by polaroids but
polarization is produced even by reflection.
13. 8. 2003
36
Polarization II
• If we cross two polaroids, ideally, no light
gets through.
• Some materials with assymetric molecules
are capable to turn the polarization plane.
• In polarographs we can measure e.g.
concentration of these.
13. 8. 2003
37
Scattering I
• Actually any atom interacts with light. Its
electrons become roughly sources of new
wavelets. We can compare it to Huygens’
principle which is valid even in vacuum.
• Since atoms are different there will be some
interaction due to superposition of waves
even for less ordered structures. But it will
be seen only in the vicinity of the 0-order
maximum.
13. 8. 2003
38
Scattering II
• Scattering again contains important
structural information.
• In atmosphere scattering behaves as 1/4.
• The sky is blue since blue light scatters most
• The sunset is red since blue waves are scattered and
just the red ones remain.
13. 8. 2003
39
Wave Limits to Geometrical
Optics I
• An image done by e.g. a lens, is in fact a
superposition of diffraction patterns. We
would find this if we display just little point.
Its image is not a point but rather diffraction
circles.
• This matters only when the magnification is
high.
13. 8. 2003
40
Wave Limits to Geometrical
Optics II
• A resolution of some optical device is
roughly a distance of two points which we
are still able to distinguish.
• If we think about the diffraction patterns the
point can be distinguished when the main
maximum of one falls into the first
minimum of the second.
13. 8. 2003
41
Homework
• No more homework from physics!
13. 8. 2003
42
Things to read and learn
• Chapters 35, 36
• Try to understand all the details of the scalar
and vector product of two vectors!
• Try to understand the physical background
and ideas. Physics is not just inserting
numbers into formulas!
13. 8. 2003
43
Maxwell’s Equations I


Q
 E  dA 
0
 
 B  dA  0
• .
 
d m
 E  dl   dt
 
d e
 B  dl   0 I encl   0 0 dt
^