* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download 1B11 Foundations of Astronomy Star names and magnitudes
Conservation of energy wikipedia , lookup
Nuclear physics wikipedia , lookup
Density of states wikipedia , lookup
Time in physics wikipedia , lookup
Electromagnetism wikipedia , lookup
Quantum electrodynamics wikipedia , lookup
Photon polarization wikipedia , lookup
Hydrogen atom wikipedia , lookup
Circular dichroism wikipedia , lookup
Wave–particle duality wikipedia , lookup
Photoelectric effect wikipedia , lookup
Theoretical and experimental justification for the Schrödinger equation wikipedia , lookup
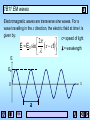
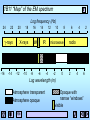
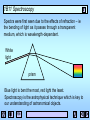
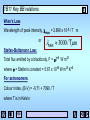
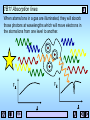
1B11 Foundations of Astronomy The Electromagnetic Spectrum Liz Puchnarewicz [email protected] www.ucl.ac.uk/webct www.mssl.ucl.ac.uk/ 1B11 The electromagnetic spectrum When an electric charge is accelerated, electromagnetic energy is produced. This energy can be thought of as propagating as a wave – or, equally as a particle. The waves are usually referred to as light waves or radiation. The particles are known as photons. 1B11 EM waves Electromagnetic waves are transverse sine waves. For a wave travelling in the x direction, the electric field at time t is given by: c= speed of light 2 E E0 sin x ct = wavelength E E0 x 0 1B11 The electromagnetic spectrum Travelling at right angles to the electric field but in the same direction, is the magnetic field, B. electric field magnetic field EM waves are self-propagating, ie they need no medium. c = speed of light in m s-1 = wavelength in m c=2.998x108 ms-1 n = frequency in Hz c n 1B11 Wave-like properties of light • Refraction – the direction of travel of light changes when light crosses the boundary from one medium to another. • Diffraction – where light waves bend when they strike the end of a barrier. • Interference – complex pattern forms when two or more wave systems combine • Polarization – where the planes in which the waves vibrate lie preferentially in one direction • Doppler Effect – where the observed wavelength, 0, is different from the emitted wavelength, , due to the velocity of the emitter, v. 0 v = obs wavelength 0 0 c 0=rest wavelength v=velocity of source 1B11 Quantum nature of light Alternatively, light can be thought of as packets (or “quanta”) of energy called photons. Photon energy, E: E hn hc n = frequency (Hz) high frequency short wavelength high energy h = Planck’s constant (6.63x10-34 Js) Examples of particle nature can be seen in: • Photo-electric effect • Atomic spectra 1B11 Units Wavelength: SI units – metre, m Optical/UV: Angstrom, A Infra-red: 1A = 10-10 m = 10-8 cm = 0.1nm nanometre, nm 1nm = 10-9 m micron, mm 1mm = 10-6 m Frequency: SI units – Hertz, Hz Radio: Gigahertz, GHz 1GHz = 109 Hz Energy: SI units – Joules, J X-ray: electron volts, eV 1eV = 1.6x10-19 J 1keV = 1.6x10-16 J 1B11 “Map” of the EM spectrum Log frequency (Hz) 24 22 20 g-rays -16 -14 18 16 UV X-rays -12 -10 14 -8 12 IR -6 -4 10 8 microwave -2 0 6 4 2 radio 2 4 6 Log wavelength (m) Atmosphere transparent Atmosphere opaque Opaque with narrow “windows” visible 1B11 Spectroscopy Spectra were first seen due to the effects of refraction – ie the bending of light as it passes through a transparent medium, which is wavelength-dependent. White light prism Blue light is bent the most, red light the least. Spectroscopy is the astrophysical technique which is key to our understanding of astronomical objects. 1B11 Kirchoff’s Rules (1824-1887) 1. A hot, dense object emits a continuous spectrum 2. A hot, transparent gas produces a spectrum of emission lines. The lines depend on the elements in the gas. 3. If a continuous spectrum passes through a transparent gas at a lower temperature, the low-T gas will superimpose dark absorption lines on the spectrum. 1B11 Continuous spectra Hot, dense objects emit a continuous blackbody spectrum. Surfaces of stars, for example, are very good “blackbodies”. Planck (1900) showed that the intensity of radiation emitted by a blackbody is: 1 hc 2 kT 5 2hc I e 1 Units: W m-2 (unit wavelength) -1 sr-1 h - Planck’s constant k – Boltzmann’s constant T – temp in Kelvin c – speed of light sr – steradian (unit of solid angle, 4 sr in a sphere) 1B11 Blackbody curves Log I 15000K Rayleigh-Jeans tail 10000K 5000K 3000K Wien tail 200 500 1000 (nm) 1B11 Key BB relations Wien’s Law: Wavelength of peak intensity, max = 2.898 x 10-3 / T m or MAX 3000 / Tmm Stefan-Boltzmann Law: Total flux emitted by a blackbody, F = sT4 W m-2 where s = Stefan’s constant = 5.67 x 10-8 W m-2 K-4 For astronomers: Colour Index, (B-V) = -0.71 + 7090 / T where T is in Kelvin 1B11 Absorption and emission lines Where do absorption and emission lines come from? The production or absorption of energy when an electron in an atom changes its level. Taking the simple case of a hydrogen atom. It has one proton in the nucleus 4 and one orbiting electron. 3 In its stable state, the 2 electron orbits in level 1 (the ground state). There 1 are an infinite number of discrete levels, converging to n= , the ionization potential. 1B11 Transitions Electron moves up n= from 2 to 3 Electron moves down from 4 to 2 n= n=6 n=5 n=4 n=6 n=5 n=4 n=3 n=3 4861A 6562A n=2 n=1 Absorption line at 6562A n=2 n=1 Emission line at 4861A 1B11 Energy levels n= n=6 n=5 n=4 Excited states Ionization potential Atoms have an infinite number of energy levels, converging to a finite value (the ionization potential). If an electron gains more energy than the ionization potential then it is no longer bound to the atom. Only the lowest level (the ground state) is generally stable. Excited states (when an electron is in level 2 or higher) have lifetimes of ~10-8 seconds. n=3 n=2 Ground state n=1 1B11 Transitions Only certain discrete energy levels are allowed for electrons in atoms. Transitions between levels are accompanied by the emission or absorption of photons. The photon energy (emitted or absorbed) corresponds to the energy lost or gained in the transition. Eb Ea Photon energy, hn = Eb - Ea 1B11 Emission lines To produce emission lines, an excited state must first be populated – when the electron in an excited state falls by one or more levels, an emission line is produced. To populate the excited levels: (a) Collisional excitation I() (b) Photo-excitation (c) Recombination hc E wavelength, These all produce emission lines and explain Kirchoff’s 2nd rule. Kirchoff’s Rules 1B11 Collisional excitation n= n=5 n=4 n=3 n=2 n=1 Collisions with electrons/ions/atoms can knock electrons into higher energy levels. The energy comes from the kinetic energy of the colliding particle. The electron falls back to lower levels and this energy is radiated away. 1B11 Photo-excitation n= n=5 n=4 n=3 n=2 n=1 If a photon with exactly the right energy interacts with an atom or ion, an electron can be moved up to a higher level for a short while, before it falls back down to the ground state. 1B11 Ionization + recombination n= OR n=1 If a photon or particle with sufficient energy interacts with an atom so that an electron is stripped away completely, it is said to be ionized. A free electron can recombine with an ion, falling into an excited state – it will then cascade down to ground level producing line emission at it falls. 1B11 Absorption lines When atoms/ions in a gas are illuminated, they will absorb those photons at wavelengths which will move electrons in the atoms/ions from one level to another. F F 1B11 Absorption lines (cont.) Atoms or ions in a gas will absorb photons whose energy corresponds exactly to the energy that an electron in that atom/ion needs to move into a higher level. After about 10-8 seconds, the electron will fall back down to the most stable state, emitting a photon with an energy corresponding to the difference between the levels, but in a random direction. So if you look through the gas at a source, you will see much few photons at that energy because these are being reemitted in random directions. This produces an absorption line and explains Kirchoff’s 3rd rule. Kirchoff’s rules 1B11 Spectrum of the hydrogen atom 13.6eV Paschen series (IR) 12.1eV Pg Pb Pa n=2 Lyman series (UV) Lyg Lyb Lya 1.9mm Balmer series (optical) Hg Hb Ha 1216A n=1 6562A 4340A n=3 4861A n=4 10.2eV En 13.60 1 1 dg b eV n 2 a 6x10-6 eV =>21cm 0eV 1B11 Astrophysical applications • Chemical composition – different atoms/molecules have different lines; line strengths indicate abundances • Ionization state – different atoms have different ionization potentials; different ions have different spectra • Temperature and density – collisional excitation in high densities; lines broadened in high-T gas • Pressure – high pressure broadens lines • State of motion – Doppler effect • Magnetic fields – in a high-B field, energy levels split due to the Zeeman effect. I I B=0 B>>0 1B11 Sources of absorption lines Stellar atmospheres star Interstellar ISM cloud gas star Intergalactic Lya systems quasar outer layers absorb blackbody emission from star 1B11 Sources of emission lines Hot ionized nebulae eg HII regions Active galactic nuclei quasar